安徽省宿州市埇桥区教育集团2022-2023学年八年级下学期期中数学试题
试卷更新日期:2023-05-09 类型:期中考试
一、单选题
-
1. 下列图形中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列式子:①;②;③;④;⑤;⑥ , 你认为其中是不等式的有( )A、2个 B、3个 C、4个 D、5个3. 如图,在中, , 过点作 , 若 , 则的大小为( )
2. 下列式子:①;②;③;④;⑤;⑥ , 你认为其中是不等式的有( )A、2个 B、3个 C、4个 D、5个3. 如图,在中, , 过点作 , 若 , 则的大小为( ) A、 B、 C、 D、4. 将多项式 加上一个单项式后,使它能够在我们所学范围内因式分解,则此单项式不能是( )A、-2 B、 C、 D、5. 如图,在△ABC中,DE是边AB的垂直平分线,垂足为E,交BC边于D点,若AC=5 cm,△ADC的周长为17 cm,则BC的长为( )
A、 B、 C、 D、4. 将多项式 加上一个单项式后,使它能够在我们所学范围内因式分解,则此单项式不能是( )A、-2 B、 C、 D、5. 如图,在△ABC中,DE是边AB的垂直平分线,垂足为E,交BC边于D点,若AC=5 cm,△ADC的周长为17 cm,则BC的长为( )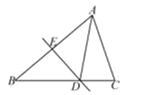 A、7 cm B、10 cm C、12 cm D、22 cm6. 如图,由绕О点旋转而得到,则下列结论不成立的是( )
A、7 cm B、10 cm C、12 cm D、22 cm6. 如图,由绕О点旋转而得到,则下列结论不成立的是( )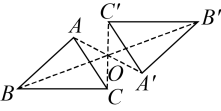 A、点A与点是对应点 B、 C、 D、7. 如图,在平面直角坐标系中,点、、在轴上,点的坐标为 , , 是经过某些变换得到的,则正确的变换是( )
A、点A与点是对应点 B、 C、 D、7. 如图,在平面直角坐标系中,点、、在轴上,点的坐标为 , , 是经过某些变换得到的,则正确的变换是( ) A、绕点逆时针旋转 , 再向下平移1个单位 B、绕点顺时针旋转 , 再向下平移1个单位 C、绕点逆时针旋转 , 再向下平移3个单位 D、绕点顺时针旋转 , 再向下平移3个单位8. 一次函数y=3x+b和y=ax-3的图象如图所示,其交点为P(-2,-5),则不等式3x+b>ax-3的解集在数轴上表示正确的是( )
A、绕点逆时针旋转 , 再向下平移1个单位 B、绕点顺时针旋转 , 再向下平移1个单位 C、绕点逆时针旋转 , 再向下平移3个单位 D、绕点顺时针旋转 , 再向下平移3个单位8. 一次函数y=3x+b和y=ax-3的图象如图所示,其交点为P(-2,-5),则不等式3x+b>ax-3的解集在数轴上表示正确的是( )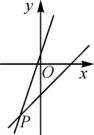 A、
A、 B、
B、 C、
C、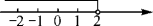 D、
D、 9. 如图,已知MN是△ABC的边AB的垂直平分线,垂足为点F,∠CAB的平分线AD交BC于点D,且MN与AD交于点O,连接BO并延长交AC于点E,则下列结论中不一定成立的是( )
9. 如图,已知MN是△ABC的边AB的垂直平分线,垂足为点F,∠CAB的平分线AD交BC于点D,且MN与AD交于点O,连接BO并延长交AC于点E,则下列结论中不一定成立的是( )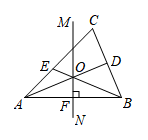 A、∠CAD=∠BAD B、OE=OF C、AF=BF D、OA=OB10. 已知关于的不等式组有且只有3个整数解,则的取值范围是( )A、 B、 C、 D、
A、∠CAD=∠BAD B、OE=OF C、AF=BF D、OA=OB10. 已知关于的不等式组有且只有3个整数解,则的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 分解因式: .12. 等腰三角形的一个底角为70°,则它的顶角的度数为 .13. 如图,正比例函数和一次函数的图象相交于点 , 当时,(填“>”或“<”)
 14. 定义新运算:对于任意实数a,b都有:a⊕b=a(a﹣b)+1,其中等式右边是通常的加法、减法及乘法运算.如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣5,那么不等式3⊕x<13的解集为 .
14. 定义新运算:对于任意实数a,b都有:a⊕b=a(a﹣b)+1,其中等式右边是通常的加法、减法及乘法运算.如:2⊕5=2×(2﹣5)+1=2×(﹣3)+1=﹣5,那么不等式3⊕x<13的解集为 .
15. 如图, , 的边在上, , , 若将绕点C逆时针旋转 , 点E的对应点N恰好落在上,则的长度为 . 16. 如图,将边长都为的正方形按如图所示的方法摆放,点分别是正方形的对称中心,则2023个这样的正方形重叠部分的面积和为 .
16. 如图,将边长都为的正方形按如图所示的方法摆放,点分别是正方形的对称中心,则2023个这样的正方形重叠部分的面积和为 .
三、解答题
-
17. 解不等式组: , 并把解集在数轴上表示出来.18. 已知a+b=2,ab=2,求 a3b+a2b2+ ab3的值.19. 如图: ,
 (1)、作出边上的中线 . (不写作法,保留作图痕迹)(2)、如果 , 请证明 .20. 如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
(1)、作出边上的中线 . (不写作法,保留作图痕迹)(2)、如果 , 请证明 .20. 如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
求证:
(1)、BC=AD;(2)、△OAB是等腰三角形.21. 在如图所示的正方形网格中,的顶点均在格点上,点A的坐标为 .
⑴画出向左平移2个单位,然后再向上平移4个单位后的;
⑵以为对称中心,画出与成中心对称的 .
