安徽省蚌埠市2022-2023学年八年级下学期G5联动教研期中调研数学试卷
试卷更新日期:2023-05-09 类型:期中考试
一、单选题
-
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 如果一个直角三角形的两条边长分别为 和 ,那么这个三角形的第三边长为( )A、 B、 C、 D、 或3. 下列方程是关于的一元二次方程的是( )A、 B、 C、 D、4. 一元二次方程x2-2x+2=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、只有一个实数根5. 在直角坐标系中,点到原点的距离是( )A、 B、 C、 D、26. 用配方法解方程 ,方程应变形为( )A、 B、 C、 D、7. 若 , 则的值为( )A、负数 B、正数 C、非零实数 D、有理数8. 某商厦10月份的营业额是50万元,第四季度的营业额是182万元.问第四季度后两个月的月平均营业额的增长率是多少?设平均增长率为 , 以下方程正确的是( )A、 B、 C、 D、9. 已知是关于x的一元二次方程的两个不相等的实数根,且满足 , 则m的值为( )A、-3或1 B、-1或3 C、-1 D、310. 如图,正方形的边长为2,其面积标记为 , 以为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为……按照此规律继续下去,则的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若关于的方程是一元二次方程,则 .12. 如图,AB=AC,则数轴上点C所表示的数为.
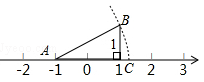 13. 已知: , 那么 .14. 如图,在正方形纸片中,是的中点,将正方形纸片折叠,点落在线段上的点处,折痕为 , 若 ,
13. 已知: , 那么 .14. 如图,在正方形纸片中,是的中点,将正方形纸片折叠,点落在线段上的点处,折痕为 , 若 ,
①则的长为 .
②则的长为 .
三、解答题
-
15. 计算:(1)、 .(2)、 .16. 用适当方法解下列方程(1)、 .(2)、 .17. 如图,在正方形网格中,小正方形的边长为1,A,B,C为格点
 (1)、判断 的形状,并说明理由.(2)、求BC边上的高.
(1)、判断 的形状,并说明理由.(2)、求BC边上的高. 18. 已知关于的方程是一元二次方程,求这个一元二次方程的解.19. 在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”译文:“有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为5尺,秋千的绳索始终拉得很直,试问绳索有多长?”
18. 已知关于的方程是一元二次方程,求这个一元二次方程的解.19. 在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”译文:“有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为5尺,秋千的绳索始终拉得很直,试问绳索有多长?” 20. 观察下列等式:①;②;③ .
20. 观察下列等式:①;②;③ .解决下列问题:
(1)、根据上面3个等式的规律,写出第⑤个式子;(2)、用含(为正整数)的等式表示上面各个等式的规律;(3)、利用上述结果计算: .21. 阅读下面的材料:解方程 , 这是一个一元四次方程,根据该方程的特点.
它的解法通常采用换元法降次:设 , 那么 , 于是原方程可变为 , 解得 , . 当时, , 所以;当时, , 所以;所以原方程有四个根: , , , .
仿照上述换元法解下列方程.
(1)、;(2)、 .22. 在蚌埠花博园附近某盆栽销售处发现:进货价为每盆50元,销售价为每盆80元的某盆栽平均每天可售出20盆.现此店决定采取适当的降价措施,扩大销售量,增加盈利.经市场调查发现:如果每盆降价2元,那么平均每天就可多售出3盆,设每盆降价x元.(1)、现在每天卖出盆,每盆盈利元(用含的代数式表示);(2)、求当为何值时,平均每天销售这种盆栽能盈利700元,同时又要使顾客得到较多的实惠;(3)、要想平均每天盈利1000元,可能吗?请说明理由.23. 如图,中, , , , 若动点从点开始,按的路径运动,且速度为每秒1cm,设出发的时间为秒.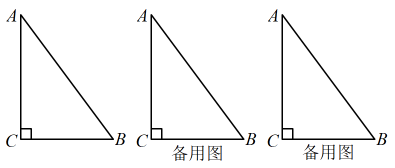 (1)、当秒时,求的周长;(2)、当在的垂直平分线上时,求的值;(3)、另有一点 , 从点开始,按的路径运动,且速度为每秒 , 若、两点同时出发,当、中有一点到达终点时,另一点也停止运动,当为何值时,直线把的周长分成相等的两部分?
(1)、当秒时,求的周长;(2)、当在的垂直平分线上时,求的值;(3)、另有一点 , 从点开始,按的路径运动,且速度为每秒 , 若、两点同时出发,当、中有一点到达终点时,另一点也停止运动,当为何值时,直线把的周长分成相等的两部分?