广东省深圳市南山区南山外国语（集团）2022-2023学年八年级下学期期中考试数学试卷

试卷更新日期：2023-05-09 类型：期中考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列图形中，可以看作是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如果x＜y，那么下列不等式正确的是（）

A、x-1＞y-1 B、x+1＞y+1 C、-2x＜-2y D、2x＜2y

查看试题解析
3. 如图，将△AOB绕点O按逆时针方向旋转45°后得到△A'OB'，若∠AOB＝15°，则∠AOB'的度数是（）

A、25° B、30° C、35° D、40°

查看试题解析
4. 若多项式x²+mx+4能用完全平方公式分解因式，则m的值可以是（　　）

A、4 B、﹣4 C、±2 D、±4

查看试题解析
5. 根据图象，可得关于x的不等式k₁x＜k₂x+b的解集是（）

A、x＜2 B、x＞2 C、x＜3 D、x＞3

查看试题解析
6. 如图，在△ABC中，AB＝AC，直线l₁∥l₂ ，且分别与△ABC的两条边相交，若∠1＝40°，∠2＝23°，则∠C的度数为（　　）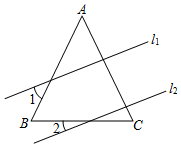

A、40° B、50° C、63° D、67°

查看试题解析
7. 下列说法正确的个数是（）
①有两条边、一个角相等的两个三角形全等；②等腰三角形的对称轴是底边上的中线；③全等三角形对应边上的中线相等；④有一个角是60°的三角形是等边三角形；⑤5cm，12cm，13cm三条长度的线段能构成直角三角形．

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，在△ABC中，已知AB＝AC，BC＝6cm，△CBD的周长为14cm，分别以A、B两点为圆心，大于 $\frac{1}{2}$ AB的长为半径画弧，两弧相交于点M，N，连接MN与AC相交于点D，则△ACB的周长为（）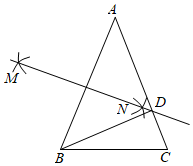

A、22cm B、16cm C、17cm D、20cm

查看试题解析
9. 不等式组 ${\begin{array}{l} 6 x + 3 > 3 (x + a) \\ \frac{x}{2} - 1 ⩽ 7 - \frac{3}{2} x \end{array}$ 的所有整数解的和为9，则整数a的值有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，在△ABC中，∠ACB＝90°，AC＝BC＝4，D为BC的中点，DE⊥AB，垂足为E．过点B作BF∥AC交DE的延长线于点F，连接CF，AF．现有如下结论：①AD平分∠CAB；②BF＝2；③AD⊥CF；④AF＝2 $\sqrt{5}$ ；⑤∠CAF＝∠CFB．其中正确的结论有（）

A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题（每题3分，共15分）

11. 已知点A（-2022，-1）与点B（a，b）关于原点O成中心对称，则a+b＝．

查看试题解析
12. 一个等腰三角形的两边长分别为4cm和8cm，则周长是 cm．

查看试题解析
13. 把多项式ax²-ay²分解因式的结果为．

查看试题解析
14. 如图，△ABC中，AD是∠BAC的平分线，BE是△ABD边AD上的中线，若△ABC的面积是24，AB＝5，AC＝3，则△ABE的面积是．

查看试题解析
15. △ABC是边长为2的等边三角形，点P为直线BC上的动点，把线段AP绕A点逆时针旋转60°至AE，O为AB边上一动点，则OE的最小值为．

查看试题解析

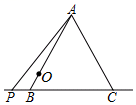
三、解答题（共55分）

16. 解不等式组，并写出该不等式组的最小整数解．
${\begin{array}{l} 5 x + 7 > 3 (x + 1) ① \\ 1 - \frac{3}{2} x ⩽ \frac{1}{2} x - 1 ② \end{array}$ ．

查看试题解析
17. 如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）．
⑴先将△ABC竖直向上平移6个单位，再水平向右平移1个单位得到△A₁B₁C₁ ，请画出△A₁B₁C₁；
⑵将△A₁B₁C₁绕B₁点顺时针旋转90°，得△A₂B₁C₂ ，请画出△A₂B₁C₂；
⑶求（2）中点A₁旋转到点A₂所经过的弧长 $\overset{⌢}{A_{1} A_{2}}$ （结果保留π）．

查看试题解析
18. 如图，在△ABC中，AB＝AC，D为AC的中点，DE⊥AB于点E，DF⊥BC于点F，且DE＝DF，连接BD，点G在BC的延长线上，且CD＝CG．

(1)、求证：△ABC是等边三角形；

(2)、若BF＝3，求CG的长．

查看试题解析
19. 某校为了更好地开展球类运动，体育组决定用1600元购进足球8个和篮球14个，已知篮球的单价比足球的单价多20元，请解答下列问题：

(1)、求出足球和篮球的单价；

(2)、若学校欲用不超过3240元，且不少于3200元再次购进两种球50个，求出有哪几种购买方案？

查看试题解析
20. 阅读材料：
①用配方法因式分解：a²+6a+8．
解：原式＝a²+6a+9-1＝（a+3）²-1＝（a+3-1）（a+3+1）＝（a+2）（a+4）．
②若M＝a²-2ab+2b²-2b+2，利用配方法求M的最小值．
解：a²-2ab+2b²-2b+2＝a²-2ab+b²+b²-2b+1+1＝（a-b）²+（b-1）²+1．
∵（a-b）²≥0，（b-1）²≥0，
∴当a＝b＝1时，M有最小值1．
请根据上述材料解决下列问题：

(1)、在横线上添上一个常数项使之称为完全平方式：a²+4a+ = ．

(2)、用配方法因式分解：a²-24a+143．

(3)、若M＝- $\frac{1}{4}$ a²+2a-1，求M的最大值．

查看试题解析
21. 已知：在△AOB和△COD中，OA＝OB，OC＝OD．

(1)、如图①，若∠AOB＝∠COD＝60°，求证：AC＝BD．

(2)、如图②，若∠AOB＝∠COD＝α，则AC与BD间的等量关系式为， ∠APB的大小为（直接写出结果，不证明）

查看试题解析
22. 如图：已知A（a，0）、B（0，b），且a、b满足（a-2）²+|2b-4|＝0．

(1)、如图1，求△AOB的面积；

(2)、如图2，点C在线段AB上（不与A、B重合）移动，AB⊥BD，且∠COD＝45°，猜想线段AC、BD、CD之间的数量关系并证明你的结论；

(3)、如图3，若P为x轴上异于原点O和点A的一个动点，连接PB，将线段PB绕点P顺时针旋转90°至PE，直线AE交y轴Q，点Q，当P点在x轴上移动时，线段BE和线段BQ中，请判断哪条线段长为定值，并求出该定值．

查看试题解析