备战2023年中考数学细点逐一突破真题训练第14章锐角三角函数及其应用
试卷更新日期:2023-05-08 类型:二轮复习
一、解直角三角形
-
1. 在中, , 则下列式子定成立的是A、 B、 C、 D、2. 在直角三角形ABC中, , 则的值是( )A、 B、 C、 D、33. 如图所示,塔底B与观测点A在同一水平面上.为了测量铁塔的高度,在A处测得塔顶C的仰角为α,塔底B与观测点A的距离为150米,则铁塔的高BC为( )
 A、150tanα米 B、米 C、sinα米 D、米
A、150tanα米 B、米 C、sinα米 D、米二、特殊角的三角函数值计算
-
4. 下列计算中错误的是( )A、 B、 C、 D、5. 如图,已知点B,D,C在同一直线的水平,在点C处测得建筑物AB的顶端A的仰角为α,在点D处测得建筑物AB的顶端A的仰角为β, , 则建筑物AB的高度为( )
 A、 B、 C、 D、6. 计算:
A、 B、 C、 D、6. 计算:三、背靠背型-实际应用
-
7. 某老年活动中心欲在一房前3m高的前墙( )上安装一遮阳篷 ,使正午时刻房前能有2m宽的阴影处( )以供纳凉,假设此地某日正午时刻太阳光与水平地面的夹角为63.4°,遮阳篷 与水平面的夹角为10°,下图为侧面示意图,请你求出此遮阳篷 的长度(结果精确到0.1m).(参考数据: , , ; , , )
 8. 某班同学在一次综合实践课上,测量校园内一棵树的高度.如图,测量仪在A处测得树顶D的仰角为45°,C处测得树顶D的仰角为37°(点A,B,C在一条水平直线上),已知测量仪高度AE=CF=1.6米,AC=28米,求树BD的高度(结果保留小数点后一位.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
8. 某班同学在一次综合实践课上,测量校园内一棵树的高度.如图,测量仪在A处测得树顶D的仰角为45°,C处测得树顶D的仰角为37°(点A,B,C在一条水平直线上),已知测量仪高度AE=CF=1.6米,AC=28米,求树BD的高度(结果保留小数点后一位.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
四、母子型-实际应用
-
9. 为传承运河文明,弘扬民族精神,枣庄市政府重建了台儿庄古城.某校“综合与实践”小组开展了测量台儿庄古城城门楼(如图①)高度的实践活动,请你帮他们完成下面的实践报告.
测量台儿庄古城城门楼高度的实践报告
活动课题
测量台儿庄古城城门楼高度
活动目的
运用三角函数知识解决实际问题
活动工具
测角仪、皮尺等测量工具
方案示意图
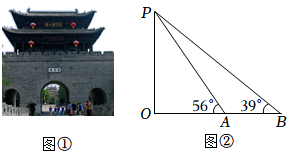
测量步骤
如图②
⑴利用测角仪站在B处测得城门楼最高点P的仰角为39°;
⑵前进了10米到达A处(选择测点A,B与O在同一水平线上,A,B两点之间的距离可直接测得,测角仪高度忽略不计),在A处测得P点的仰角为56°.
参考数据
sin39°≈0.6,cos39°≈0.8,tan39°≈0.8,sin56°≈0.8,cos56°≈0.6,tan56°≈1.5.
计算城门楼PO的高度(结果保留整数)
10. 胜利黄河大桥犹如一架巨大的竖琴,凌驾于滔滔黄河之上,使黄河南北“天堑变通途”.已知主塔垂直于桥面于点B,其中两条斜拉索与桥面的夹角分别为和 , 两固定点D、C之间的距离约为 , 求主塔的高度(结果保留整数,参考数据:) 11. 为了学生的安全,某校决定把一段如图所示的步梯路段进行改造.已知四边形 为矩形, ,其坡度为 ,将步梯 改造为斜坡 ,其坡度为 ,求斜坡 的长度.(结果精确到 ,参考数据: , )
11. 为了学生的安全,某校决定把一段如图所示的步梯路段进行改造.已知四边形 为矩形, ,其坡度为 ,将步梯 改造为斜坡 ,其坡度为 ,求斜坡 的长度.(结果精确到 ,参考数据: , )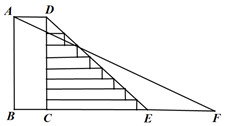 12. 如图,小睿为测量公园的一凉亭AB的高度,他先在水平地面点E处用高1.5m的测角仪DE测得 ,然后沿EB方向向前走3m到达点G处,在点G处用高1.5m的测角仪FG测得 .求凉亭AB的高度.(A,C,B三点共线, , , , .结果精确到0.1m)(参考数据: , , , , , )
12. 如图,小睿为测量公园的一凉亭AB的高度,他先在水平地面点E处用高1.5m的测角仪DE测得 ,然后沿EB方向向前走3m到达点G处,在点G处用高1.5m的测角仪FG测得 .求凉亭AB的高度.(A,C,B三点共线, , , , .结果精确到0.1m)(参考数据: , , , , , ) 13. 我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点A处时,在P处测得A点的仰角 为 且A与P两点的距离为6千米,它沿铅垂线上升75秒后到达B处,此时在P处测得B点的仰角 为 ,求天舟二号从A处到B处的平均速度.(结果精确到 ,取 )
13. 我国航天事业捷报频传,天舟二号于2021年5月29日成功发射,震撼人心.当天舟二号从地面到达点A处时,在P处测得A点的仰角 为 且A与P两点的距离为6千米,它沿铅垂线上升75秒后到达B处,此时在P处测得B点的仰角 为 ,求天舟二号从A处到B处的平均速度.(结果精确到 ,取 )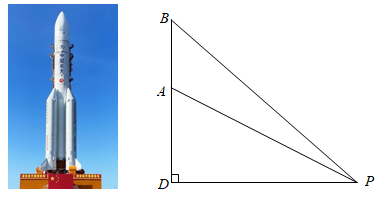
五、拥抱型-实际应用
-
14. 如图,在一次数学实践活动中,小明同学要测量一座与地面垂直的古塔 的高度,他从古塔底部点B处前行 到达斜坡 的底部点C处,然后沿斜坡 前行 到达最佳测量点D处,在点D处测得塔顶A的仰角为 ,已知斜坡的斜面坡度 ,且点A,B,C,D,E在同一平面内,小明同学测得古塔 的高度是( )
 A、 B、 C、 D、15. 在一次综合实践活动中,某小组对一建筑物进行测量.如图,在山坡坡脚C处测得该建筑物顶端B的仰角为60°,沿山坡向上走20m到达D处,测得建筑物顶端B的仰角为30°.已知山坡坡度 , 即 , 请你帮助该小组计算建筑物的高度 . (结果精确到0.1m,参考数据:)
A、 B、 C、 D、15. 在一次综合实践活动中,某小组对一建筑物进行测量.如图,在山坡坡脚C处测得该建筑物顶端B的仰角为60°,沿山坡向上走20m到达D处,测得建筑物顶端B的仰角为30°.已知山坡坡度 , 即 , 请你帮助该小组计算建筑物的高度 . (结果精确到0.1m,参考数据:)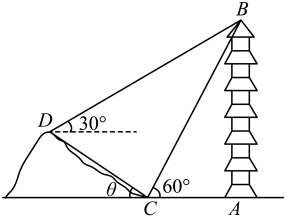 16. 在全民健身运动中,骑行运动颇受市民青睐.一市民骑自行车由A地出发,途经B地去往C地,如图.当他由A地出发时,发现他的北偏东 方向有一信号发射塔P.他由A地沿正东方向骑行 km到达B地,此时发现信号塔P在他的北偏东 方向,然后他由B地沿北偏东 方向骑行12km到达C地.
16. 在全民健身运动中,骑行运动颇受市民青睐.一市民骑自行车由A地出发,途经B地去往C地,如图.当他由A地出发时,发现他的北偏东 方向有一信号发射塔P.他由A地沿正东方向骑行 km到达B地,此时发现信号塔P在他的北偏东 方向,然后他由B地沿北偏东 方向骑行12km到达C地. (1)、求A地与信号发射塔P之间的距离;(2)、求C地与信号发射塔P之间的距离.(计算结果保留根号)17. 小明周末与父母一起到遂宁湿地公园进行数学实践活动,在A处看到B、C处各有一棵被湖水隔开的银杏树,他在A处测得B在北偏西45°方向, C在北偏东30°方向,他从A处走了20米到达B处,又在B处测得C在北偏东60°方向.
(1)、求A地与信号发射塔P之间的距离;(2)、求C地与信号发射塔P之间的距离.(计算结果保留根号)17. 小明周末与父母一起到遂宁湿地公园进行数学实践活动,在A处看到B、C处各有一棵被湖水隔开的银杏树,他在A处测得B在北偏西45°方向, C在北偏东30°方向,他从A处走了20米到达B处,又在B处测得C在北偏东60°方向. (1)、求∠C的度数;(2)、求两颗银杏树B、C之间的距离(结果保留根号).
(1)、求∠C的度数;(2)、求两颗银杏树B、C之间的距离(结果保留根号).六、综合应用型
-
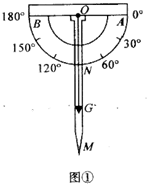
18. 某数学兴趣小组自制测角仪到公园进行实地测量,活动过程如下:(1)、探究原理制作测角仪时,将细线一段固定在量角器圆心 处,另一端系小重物 .测量时,使支杆 、量角器90°刻度线 与铅垂线 相互重合(如图①),绕点 转动量角器,使观测目标 与直径两端点 共线(如图②),此目标 的仰角 .请说明两个角相等的理由.
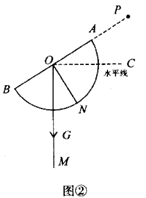 (2)、实地测量
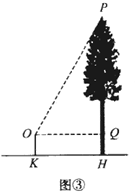
(2)、实地测量如图③,公园广场上有一棵树,为了测量树高,同学们在观测点 处测得顶端 的仰角 ,观测点与树的距离 为5米,点 到地面的距离 为1.5米;求树高 . ( ,结果精确到0.1米)
 (3)、拓展探究
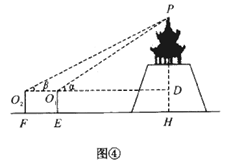
(3)、拓展探究公园高台上有一凉亭,为测量凉亭顶端 距离地面高度 (如图④),同学们讨论,决定先在水平地面上选取观测点 ( 在同一直线上),分别测得点 的仰角 ,再测得 间的距离 ,点 到地面的距离 均为1.5米;求 (用 表示).
 19. 如图1是钢琴缓降器,图2和图3是钢琴缓降器两个位置的示意图.是缓降器的底板,压柄可以绕着点B旋转,液压伸缩连接杆的端点分别固定在压柄与底板上,已知 .
19. 如图1是钢琴缓降器,图2和图3是钢琴缓降器两个位置的示意图.是缓降器的底板,压柄可以绕着点B旋转,液压伸缩连接杆的端点分别固定在压柄与底板上,已知 . (1)、如图2,当压柄与底座垂直时,约为 , 求的长;(2)、现将压柄从图2的位置旋转到与成角(即),如图3的所示,求此时液压伸缩连接杆的长.(结果保留根号)
(1)、如图2,当压柄与底座垂直时,约为 , 求的长;(2)、现将压柄从图2的位置旋转到与成角(即),如图3的所示,求此时液压伸缩连接杆的长.(结果保留根号)(参考数据:;)
20. 综合与实践:在学习《解直角三角形》一章时,小邕同学对一个角的倍角的三角函数值与这个角的三角函数值是否有关系产生了浓厚的兴趣,并进行研究.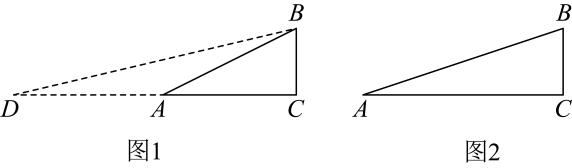 (1)、【初步尝试】我们知道: , .
(1)、【初步尝试】我们知道: , .发现:(填“”或“”).
(2)、【实践探究】在解决“如图1,在中, , , , 求的值”这一问题时,小邕想构造包含的直角三角形,延长到点D,使 , 连接BD,所以可得 , 问题即转化为求的正切值,请按小邕的思路求的值.(3)、【拓展延伸】如图2,在中, , , .请模仿小邕的思路或者用你的新思路,试着求一求的值.