2023年湖北省黄冈、孝感、咸宁三地中考模拟数学试卷

试卷更新日期：2023-05-06 类型：中考模拟

进入出卷网下载

一、单选题（每题3分，共24分）

1. $- \frac{1}{2023}$ 的绝对值是（）

A、-2023 B、2023 C、 $\frac{1}{2023}$ D、 $- \frac{1}{2023}$

查看试题解析
2. 2月5日，合肥市统计局发布2022年全市经济运行情况．根据地区生产总值统一核算结果，2022年合肥全市生产总值（ $G D P$ ）为12013.1亿元，连续七年每年跨越一个千亿台阶．数据12013.1亿用科学记数法表示为（）

A、 $1.20131 \times 1 0^{8}$ B、 $12.0131 \times 1 0^{12}$ C、 $0.120131 \times 1 0^{13}$ D、 $1.20131 \times 1 0^{12}$

查看试题解析
3. 如图， $∠ A C E$ 是 $Δ A B C$ 的外角， $∠ A C D = ∠ A$ ， $∠ B = 50 °$ ，则 $∠ B C D$ 的度数为（）

A、 $130 °$ B、 $120 °$ C、 $110 °$ D、 $100 °$

查看试题解析
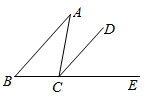4. 一个几何体的三视图如图所示，其中俯视图为正三角形，则该几何体的左视图中a的值为（）

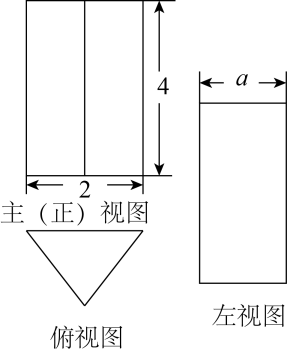A、2 B、 $\sqrt{3}$ C、1.7 D、1.8

查看试题解析
5. 在平面直角坐标系中，点 $(a - 3 ， 4)$ 关于原点的对称点为 $(5 ， - b)$ ，则 $a b$ 的值为（）

A、 $- 8$ B、8 C、6 D、 $- 12$

查看试题解析
6. 如图，AB是⊙O的直径，点C、D在⊙O上，连接AD、CD，若∠C＝28°，则若∠A的大小为（）

A、30° B、28° C、24° D、34°

查看试题解析
7. 如图，在Rt△ABC中，∠B＝90°，分别以点A和点C为圆心，大于 $\frac{1}{2}$ AC的长为半径画弧，两弧相交于点E，点F，作直线EF交BC于点D，连接AD，若AB＝3，BC＝5，则△ABD的周长为（　　）

A、5 B、6 C、7 D、8

查看试题解析
8. 抛物线 $y = a x^{2} + b x + c$ 与x轴的公共点是（-1，0），（3，0），直线 $y = k x + m$ 经过点（-1，0），直线 $y = k x + m$ 与抛物线 $y = a x^{2} + b x + c$ 另一个交点的横坐标是4，它们的图象如图所示，有以下结论：①抛物线对称轴是 $x = 1$ ；② $a - b + c = 0$ ；③ $- 1 < x < 3 时， a x^{2} + b x + c < 0 ；$ ④ $若 a = \frac{1}{2} ，则 k = \frac{1}{2}$ 。
其中正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题（每空3分，共24分）

9. ${(\sqrt{3} - 1.732)}^{0} + {(- \frac{1}{4})}^{- 2} =$ ．

查看试题解析
10. 函数y＝ $\frac{1}{\sqrt{x - 2}} + \sqrt{4 - x}$ 中自变量的取值范围是.

查看试题解析
11. 如图，在矩形ABCD中，AB＝1，∠DBC＝30°.若将BD绕点B旋转后，点D落在BC延长线上的点E处，点D经过的路径为弧DE，则图中阴影部分的面积为.

查看试题解析
12. 2022年中考模拟体育测试中，我区某校随机抽取了10名男生的引体向上成绩，将这组数据整理后制成如下统计表，下列说法中正确的是．（填序号）
①这组数据的众数是8；
②这组数据的中位数是7；
③这组数据的平均数是7；
④这组数据的方差是2.2
成绩（次）
9
8
6
5
人数（名）
2
3
3
2

查看试题解析
13. 设 $α$ ， $β$ 是一元二次方程 $x^{2} + 3 x - 7 = 0$ 的两个根，则 $a^{2} + 4 α + β =$ ．

查看试题解析
14. 如图，同学们利用所学知识去测量三江源某河段某处的宽度，小童同学在A处观测对岸点C，测得 $∠ C A D = 45 °$ ，小郑同学在距点A处 $60$ 米远的B点测得 $∠ C B D = 30 °$ ，请计算：河宽米.（精确到 $0.01$ 米， $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732$ ）

查看试题解析
15. 定义一种对正整数n的“F”运算：①当n为奇数时，结果为3n＋5；②当n为偶数时，结果为 $\frac{n}{2^{k}}$ (其中k是使 $\frac{n}{2^{k}}$ 为奇数的正整数)，运算重复进行下去．例如：取n＝26，运算如图3－3－9所示．

图3－3－9
若n＝449，则第449次“F”运算的结果是．

查看试题解析
16. 如图，正方形 $A B C D$ 的边长为4，E，F分别是边 $A D 、 D C$ 上的动点，且 $A E = D F$ ，连接 $A F ， B E$ 交于点G，P是 $A D$ 边上的另一个动点，连接 $P G ， P C$ ，则 $P G + P C$ 的最小值为.

查看试题解析

三、解答题（共8题，共72分）

17. 先化简，再求值： $(\frac{3}{x + 1} - x + 1) \div \frac{x^{2} - 4 x + 4}{x + 1}$ ，其中 $x = 3$ .

查看试题解析
18. 甲、乙两人准备整理一批新到的实验器材，若甲单独整理需要40分钟完工，若甲、乙共同整理20分钟后，乙需再单独整理20分钟才能完工.

(1)、问乙单独整理多少分钟完工？

(2)、若乙因工作需要，他的整理时间不超过30分钟，则甲至少整理多少分钟才能完工？

查看试题解析
19. 如图， $A B$ 是 $⊙ O$ 的直径， $A C$ 是 $⊙ O$ 的弦， $A D$ 平分 $∠ C A B$ 交 $⊙ O$ 于点D，过点D作 $⊙ O$ 的切线 $E F$ ，交 $A B$ 的延长线于点E，交 $A C$ 的延长线于点F.

(1)、求证： $A F ⊥ E F$ ；

(2)、若 $A C = 2 ， A B = 4$ ，求 $B E$ 的长.

查看试题解析
20. 某校为落实“双减”政策，增强课后服务的丰富性，充分用好课后服务时间，3月份学校开展数学学科活动，其中七年级开展了五个项目（每位学生只能参加一个项目）：A．阅读数学名著；B．讲述数学故事；C．制作数学模型；D．参与数学游戏；E．挑战数学竞赛．为了解学生对以上活动的参与情况，随机抽取部分学生进行了调查统计，并根据统计结果，绘制了如图所示的两幅不完整的统计图．
根据图中信息，解答下列问题：

(1)、①此次调查一共随机抽取了 ▲ 名学生；
②补全条形统计图（要求在条形图上方注明名数）；
③扇形统计图中圆心角 $α =$ ▲ 度；

(2)、若该年级有1100名学生，请你估计该年级参加D项目的学生大约有多少名；

(3)、在C项目展示活动中，某班获得一等奖的学生有3名男生，2名女生，则从这5名学生中随机抽取2名学生代表本班参加学校制作数学模型活动，请直接写出恰好抽到2名男生的概率．

查看试题解析
21. 如图，直线 $y_{1} = - x + 4$ ， $y_{2} = \frac{3}{4} x + b$ 都与双曲线 $y = \frac{k}{x}$ 交于点 $A (1 ， m)$ ，这两条直线分别与x轴交于B，C两点．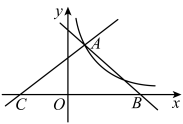

(1)、求y与x之间的函数关系式；

(2)、直接写出当 $x > 0$ 时，不等式 $- x + 4 > \frac{k}{x}$ 的解集；

(3)、若点P在x轴上，连接 $A P$ 把 $△ A B C$ 的面积分成 $1 ： 3$ 两部分，求此时点P的坐标．

查看试题解析
22. 小黄做小商品的批发生意，其中某款“中国结”每件的成本为15元，该款“中国结”的批发单价y（元）与一次性批发量x（x为正整数）（件）之间满足如图所示的函数关系．

(1)、当 $200 \leq x \leq 400$ 时，求y与x的函数关系式．

(2)、某零售商在小黄处一次性批发该款“中国结”，共支付7280元，求此次批发量．

(3)、某零售商在小黄处一次性批发该款“中国结”x（ $200 \leq x \leq 600$ ）件，小黄获得的利润为w元，当x为何值时，小黄获得的利润最大？最大利润是多少元？

查看试题解析
23. 如图1，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ，点D是边 $A B$ 的中点，连接 $C D$ ， $C D = 6$ ，以点D为顶点作 $△ D E F$ ，使 $∠ E D F = 90 °$ ， $D E = D F = 10$ ．

(1)、连接 $B F$ ， $C E$ ．线段 $B F$ 和线段 $C E$ 的数量关系为，直线 $B F$ 和直线 $C E$ 的位置关系为；

(2)、如图2，当 $E C ∥ A B$ 时，设 $A C$ 与 $D E$ 交于点G，求 $D G$ 的长度；

(3)、当E，C，B在同一条直线上时，请直接写出 $C E$ 的长度．

查看试题解析
24. 图1，在平面直角坐标系 $x O y$ 中，已知抛物线 $y = - x^{2} + b x + c$ 经过 $A (- 1 ， 0)$ ， $B (3 ， 0)$ 两点．P是抛物线上一点，且在直线 $B C$ 的上方．

(1)、求抛物线的解析式；

(2)、如图2，点E为 $O C$ 中点，作 $P Q ∥ y$ 轴交 $B C$ 于点Q，若四边形 $C P Q E$ 为平行四边形，求点P的横坐标；

(3)、如图3，连结 $A C 、 A P$ ， $A P$ 交 $B C$ 于点M，作 $P H ∥ A C$ 交 $B C$ 于点H．记 $△ P H M$ ， $△ P M C$ ， $△ C A M$ 的面积分别为 $S_{1} ， S_{2} ， S_{3}$ ．判断 $\frac{S_{1}}{S_{2}} + \frac{S_{2}}{S_{3}}$ 是否存在最大值，若存在，求出最大值；若不存在，请说明理由．

查看试题解析

成绩（次）	9	8	6	5
人数（名）	2	3	3	2