浙江省温州市瑞安市集云北外等校2022-2023 学年八年级下学期中质量检测数学试卷

试卷更新日期：2023-05-06 类型：期中考试

进入出卷网下载

一、选择题(本题有10小题，每小题3分，共30分．)

1. 下图中的各车标图案，是中心对称图形的共有（）个

A、4 B、3 C、2 D、1

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{5} = \sqrt{7}$ B、 $2 \sqrt{3} - \sqrt{3} = 2$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $\sqrt{6} \div 3 = \sqrt{2}$

查看试题解析
3. 某校八年级45位同学参加数学竞赛，每位同学分数各不相同，按成绩取前23名进入决赛，若知道某同学分数，要判断这名同学能否进决赛，只需知道45位同学分数的（）

A、众数 B、中位数 C、平均数 D、方差

查看试题解析
4. 各个内角都相等的n边形的一个外角为20°，则n等于（）

A、9 B、16 C、18 D、20

查看试题解析
5. 用反证法证明“三角形三个内角中至少有一个角不大于60°”时，首先应假设（）

A、三角形三个内角中至多有一个角不大于60° B、三角形三个内角中至少有一个角不小于60 C、三角形三个内角中至少有一个角大于60° D、三角形三个内角都大于60°

查看试题解析
6. 用配方法将方程x²-4x+3= 0化成(x+a)²=b的形式，则b的值是（）

A、1 B、-1 C、7 D、-7

查看试题解析
7. 关于x的一元二次方程x²+kx+k-1=0的根的情况，下列说法中正确的是（）

A、有两个实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、无实数根

查看试题解析
8. 受电子商务的发展及国家法治环境改善等因素的影响，某公司快递业务量迅猛发展，2020年公司快递业务量为200万件，2022年快递业务量达到288万件，若设快递量平均每年增长率为x，则下列方程中，正确的是（）

A、200(1+2x)=288 B、200(1+x)²=288 C、200(1+x²)=288 D、200(1+2x)²=288

查看试题解析
9. 如图，四边形ABCD的两条对角线AC、BD交于点O，下列条件不能判定四边形ABCD是平行四边形的是（）

A、AO=CO，BO=DO B、AB=CD，AD=BC C、AB∥CD，AB=CD D、AB∥CD，AD=BC

查看试题解析
10. 如图， $▱$ ABCD中，AB=22cm，BC= $8 \sqrt{2}$ cm，∠A=45°，动点E从A出发，以2cm/s的速度沿AB向点B运动，动点F从点C出发，以1cm/s的速度沿着CD向D运动，当点E到达点B时，两个点同时停止．则EF的长为10cm时点E的运动时间是（）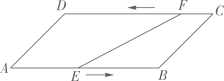

A、6s B、6s或10s C、8s D、8s或12s

查看试题解析

二、填空题(本题有8小题，每小题3分，共24分)

11. 要使二次根式 $\sqrt{a + 3}$ 有意义，则字母a的取值范围是

查看试题解析
12. 当a=-2时，二次根式 $\sqrt{2 - a}$ 的值是．

查看试题解析
13. 已知关于x的一元二次方程x²+mx+m²-4=0有一个根是0，则m=

查看试题解析
14. 有一块长方形木板，木工采用如图所示的方式，在木板上截出两个面积分别为18dm²和32dm²的正方形木板，则剩余木料(阴影部分)的面积为dm² ．

查看试题解析
15. 如图，在四边形ABCD中，点E、F分别是AB、AD边的中点，∠BCD=90°，BC=6，EF=5，则CD的长为

查看试题解析
16. 如图， $▱$ ABCD中，E是AD边上的一点，将△ABE沿BE翻折得到△A'BE，点A'恰好落在 $▱$ ABCD的对角线BD上，且DE=DA'．若∠C=100°，则∠ABE的度数是

查看试题解析
17. 如图，四边形ABCD中，若AB= AD=5，BD=8，∠ABD=∠CDB，则△ABC的面积为

查看试题解析
18. 如图，在 $▱$ ABCD中，AB=V2，BC=√6，∠ABC=60° ，分别以 $▱$ ABCD的各边为边向外作正方形，顺次连结四个正方形的对称中心，得到四边形EFGH，则四边形EFGH面积为

查看试题解析

三、解答题(本题有6小题，共46分)

19.

(1)、计算： $\sqrt{16} - \sqrt{25} + \sqrt{(- 3)^{2}}$

(2)、解方程： x²-3x=0

查看试题解析
20. 如图，在方格纸中按要求画一个以A，B，C，D为顶点的平行四边形．(图中每个小方格的边长为1，点A，B，C，D都必须在格点上)

(1)、在图1中画一个 $▱$ ABCD，使∠ABC=135°， BC= 3．

(2)、在图2中画一个 $▱$ ABCD，使各边长均为无理数，且该平行四边形的面积为 6．

查看试题解析
21. 在学校组织的“建最美校园，做最美学生”知识竞赛中，每班参加比赛的人数相同，成绩分为A、B、C、D四个等级，其中相应等级的得分依次记为100分、90分、80分、70分，学校将某年级的一班和二班的成绩整理并绘制成如下的统计图：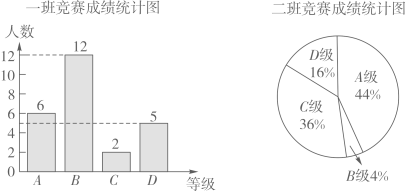
请你根据以上提供的信息解答下列问题：

(1)、此次竞赛中二班在C级以上(包括C级)的人数是多少人？

(2)、请你将表格补充完整：

平均分
中位数
众数
一班
90
二班
87.6
100

查看试题解析
22. 如图，在 $▱$ ABCD中，O为AC的中点，EF过点O，分别交AD，CB的延长线于点E，F．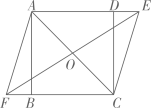

(1)、求证：四边形AFCE是平行四边形．

(2)、若AC平分∠BAE，AB=5，AE=7，求BF的长．

查看试题解析

23. 根据以下素材，探索完成任务。

圆柱体外包装的材料损耗率问题研究
素材1	厂商在生产产品时，对产品外包装的材料，通常要考虑尽可能地合理利用，减少浪费。圆柱体形状的物品，它的外包装盒通常都是长方体，且上下底面为正方形。
素材2	设计产品外包装时，我们把裁剪掉的废料部分的面积与原图形的面积之比称为材料的损耗率。一种材料利用率较高的裁剪方式如图所示，采用正方形纸板裁剪，只需剪掉四条边上的四个小三角形。按这种方式包装一个底面直径为2，高为1的圆柱体(接缝处的材料损耗不计)，损耗率只有 $\frac{2}{18}$ ≈11.1%．
	问题解决
任务1	现采用一张边长为4 $\sqrt{2}$ cm的正方形纸，按如图所示的裁剪方式剪掉各边上的四个三角形后，可恰好无缝地做成一个圆柱体的外包装盒，设圆柱体的底面半径为r，则它的高h= ▲ (用r的代数式表示)
任务2	在上图中，若已知该圆柱体外包装盒的材料损耗率为16%，求这个圆柱体的底面半径r
任务3	现利用两块同样大小的正方形纸板，按如图方式裁剪后，可包装两个高分别为4和2的圆柱体，发现这两个圆柱体的体积恰好相等．求第一个圆柱体的底面半径．(圆柱体的体积=底面积×高)

查看试题解析

24. 如图1，在直角坐标系中，直线y=-2x+8交x轴于点B，交y轴于点A， C是AB的中点，动点P从点A出发沿AO方向以每秒1个单位的速度向终点O运动，同时动点Q从点O出发以每秒2个单位的速度沿射线OB方向运动．以CP，CQ为边构造 ▱ CPDQ，设点P运动的时间为t秒．

(1)、写出点C的坐标和直线OC的解析式．
点C的坐标是，直线OC的解析式是

(2)、如图2，当点Q运动到点B时，连结CD．求证： CD∥AP．

(3)、连结OC．当点D落在△AOC的边上或各边所在的直线上时，求t的值．

查看试题解析

	平均分	中位数	众数
一班		90
二班	87.6		100