浙江省湖州市长兴县2022-2023学年七年级下学期4月期中数学试题
试卷更新日期：2023-05-06 类型：期中考试
一、选择题(每小题3分，共30分)
-
1. 计算结果等于2的是（ ）A、|-2| B、-|2| C、2-1 D、(-2)02. 如图．已知直线a，b被直线c所截，且a∥b，∠1=48°，那么∠2的度数为（ ）
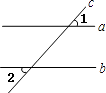A、42° B、48° C、52° D、132°3. 将方程3x+y=9写成用含y的式子表示x的形式，正确的是（ ）A、y=3x-9 B、y=9-3x C、x=-3 D、x=3-4. 下列运算正确的是（ ）A、a2+2a2=3a4 B、(2a2)3=8a6 C、a3·a2=a6 D、(a-b)2=a2-b25. 已知是二元一次方程x-y=10的解，则k的值是（ ）A、-10 B、-2 C、2 D、106. 若(2x-m)(x+ 1)的运算结果中不含x的一次项，则m的值等于（ ）A、2 B、1 C、-1 D、-27. 在学习平行线知识时，甲同学认为“经过一点有且只有一条直线与已知直线平行”；乙同学认为“垂直于同--条直线的两条直线互相平行”，则下列判断正确的是（ ）A、甲正确，乙错误 B、甲错误，乙正确 C、甲乙都正确 D、甲乙都错误8. 如图，在边长为1的小正方形组成的网格中，点A，B，C都在格点上，若将线段AB沿BC方向平移，使点B与点C重合，则线段AB扫过的面积为（ ）
A、8 B、9 C、10 D、119. 已知x-y=7，xy=5，则(x+1)(1-y)的值为（ ）A、13 B、-13 C、-11 D、310. 小双制作了如图所示的卡片A类，B类，C类各50张，其中A，B两类卡片都是正方形，C类卡片是长方形，现要拼一个长为(5a+7b)，宽为(7a+b)的大长方形，那么所准备的C类卡片的张数（ ）
A、够用，剩余4张 B、不够用，还缺4张 C、够用，剩余5张 D、不够用，还缺5张二、填空题(每小题2分，共12分)
-
11. 将0.00126用科学记数法表示为12. 计算：.13. 计算：(-2)3×=14. 关于x，y的二元一次方程组 ， 小华用加减消元法消去未知数x，按照他的思路，用②×2-①得到的方程是15. 如图，△ABC中，∠B=40°，点D为边BC上一点，将△ADC沿直线AD折叠后，点C落到点E处，若DE∥AB，则∠ADE的度数为°．
16. 公式S=mx+ny-1可以用来求正方形网格中顶点为格点的多边形面积，其中x表示多边形内部格点数，y表示多边形边上格点数．例如：图中三角形ABC中，x=1，y=4，S=2；图中三角形DEF中，x=0，y=6，S=2．请借助上面提供的网格求出x=20，y=10时，S=
三、解答题(共58分)
-
17. 计算：(1)、x·(-x)2；(2)、(π-3)0-()-2 ．18. 解方程组：(1)、(2)、19. 先化简，再求值：(2x+1)(2x-1)-(2x-3)2 ， 其中x=-2．20. 已知a+b=3，ab=-2，求下列各式的值：(1)、a2+b2；(2)、9a·27b÷3b ．21. 如图，在△ABC中，CD⊥AB于点D，EF⊥CD于点G，∠ADE=∠EFC．
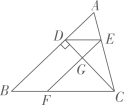(1)、请说明∠B=∠EFC的理由；(2)、若∠A=60°，∠ACB=76°，求∠CDE的度数．22. 小减同学计算一道整式乘法：(3x+a)(2x+3)，由于他抄错了多项式中a前面的符号，把“+”写成“-”，得到的结果为6x2+bx-6．(1)、求a，b的值；(2)、计算这道整式乘法的正确结果．23. 小双老师为了检测同学们上课的听课效果，采用一道课本 例题考考大家：用如图一中的长方形和正方形纸板作侧面和底面，做成如图二的竖式和横式两种无盖纸盒，现在仓库里有1000张正方形纸板和2000张长方形纸板．
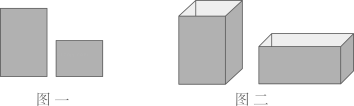(1)、根据题意完成下表．x只竖式纸盒中
y只横式纸盒中
合计
正方形纸板的张数
1000
长方形纸板的张数
2000
(2)、问两种纸盒各做多少个，恰好将库存的纸板用完？24. 如图，已知点E在DB的延长线上，AB∥CD，CD平分∠ACF．
(1)、若∠EBA与∠A互补，∠EBA=40°，求∠ACF的度数；(2)、若2∠EBA+∠A=180°，探究并写出∠EBA与∠ACF的数量关系；(3)、若k∠EBA+∠A=180°．∠EBA=∠ACF，求k：t的值．