浙江省温州市龙港区2023年中考数学一模试卷
试卷更新日期:2023-05-06 类型:中考模拟
一、单选题
-
1. 计算的结果是( )A、10 B、5 C、-5 D、-102. 太阳半径约696000000米,其中数据696000000科学记数法表示为( )A、 B、 C、 D、3. 从边长为2cm的立方体中挖去边长为1cm的立方体,得到的几何体如图所示,它的左视图是( )
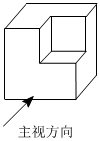 A、
A、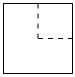 B、
B、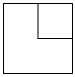 C、
C、 D、
D、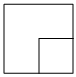 4. 计算的结果是( )A、 B、 C、 D、5. 对温州某学生上月消费情况进行问卷调查后,绘制成如图所示统计图.已知他在交通上花费了60元,那么在学习用品上花费了( )
4. 计算的结果是( )A、 B、 C、 D、5. 对温州某学生上月消费情况进行问卷调查后,绘制成如图所示统计图.已知他在交通上花费了60元,那么在学习用品上花费了( ) A、30元 B、60元 C、90元 D、120元6. 如图,已知A,B的坐标分别为 , , 将沿x轴正方向平移,使B平移到点E,得到 , 若 , 则点C的坐标为( )
A、30元 B、60元 C、90元 D、120元6. 如图,已知A,B的坐标分别为 , , 将沿x轴正方向平移,使B平移到点E,得到 , 若 , 则点C的坐标为( ) A、 B、 C、 D、7. 《孙子算经》中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四足五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余 尺.将绳子对折再量长木,长木还剩余 尺,问木长多少尺,现设绳长 尺,木长 尺,则可列二元一次方程组为( )A、 B、 C、 D、8. 图1是一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形, , 则双翼边缘端点C与D之间的距离为( )
A、 B、 C、 D、7. 《孙子算经》中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四足五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余 尺.将绳子对折再量长木,长木还剩余 尺,问木长多少尺,现设绳长 尺,木长 尺,则可列二元一次方程组为( )A、 B、 C、 D、8. 图1是一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形, , 则双翼边缘端点C与D之间的距离为( ) A、 B、 C、 D、9. 已知二次函数 , 关于该函数在的取值范围内有最大值-1,a可能为( )A、-2 B、-1 C、0.5 D、1.510. 如图,在正方形ABCD中,P是AB上一点,连接CP,DP,正方形EFGH的顶点E,F落在AB上,G,H分别落在CP,DP上,射线AH交射线BG于点分别记 , , 的面积为 , , , 已知HG::5,若 , 则的值为( )
A、 B、 C、 D、9. 已知二次函数 , 关于该函数在的取值范围内有最大值-1,a可能为( )A、-2 B、-1 C、0.5 D、1.510. 如图,在正方形ABCD中,P是AB上一点,连接CP,DP,正方形EFGH的顶点E,F落在AB上,G,H分别落在CP,DP上,射线AH交射线BG于点分别记 , , 的面积为 , , , 已知HG::5,若 , 则的值为( )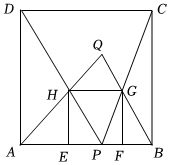 A、8 B、12 C、16 D、20
A、8 B、12 C、16 D、20二、填空题
-
11. 分解因式: .12. 不透明的袋子中只有4个黑球和2个白球,这些球除颜色外无其他差别,随机从袋子中摸出1个球是白球的概率为 .13. 不等式组的解为 .14. 如图,四边形ABCD是的内接四边形,BE是的直径,连结CE,若 , 则 度.
 15. 两个形状大小相同的菱形在矩形ABCD内按如图所示方式摆放,若菱形的边长为2cm, , 且 , 则AD的长为
15. 两个形状大小相同的菱形在矩形ABCD内按如图所示方式摆放,若菱形的边长为2cm, , 且 , 则AD的长为 16. 图1是一种可调节桌面画架,画架侧面及相关数据如图2所示是底座OA上一固定支点,点C在滑槽DE内滑动,支杆BC长度不变.已知 , 当C从点D出发滑向终点E,从逐渐增大至 , 则支杆BC的长为 cm,若点F到OA的距离为40cm,则
16. 图1是一种可调节桌面画架,画架侧面及相关数据如图2所示是底座OA上一固定支点,点C在滑槽DE内滑动,支杆BC长度不变.已知 , 当C从点D出发滑向终点E,从逐渐增大至 , 则支杆BC的长为 cm,若点F到OA的距离为40cm,则
三、解答题
-
17.(1)、计算:;(2)、化简:18. 如图,是等边三角形,D是边AB上一点,以CD为边作E等边 , DE交AC于点F,连接AE,
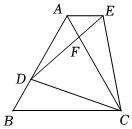 (1)、求证:≌(2)、若 , , 求CD的长.19. 保温杯的保温时效是顾客购买保温杯时的首要考虑因素.随机选择A款保温杯20个,B款保温杯20个.统计了每一个保温杯的保温时效,并绘制成如下统计图表.
(1)、求证:≌(2)、若 , , 求CD的长.19. 保温杯的保温时效是顾客购买保温杯时的首要考虑因素.随机选择A款保温杯20个,B款保温杯20个.统计了每一个保温杯的保温时效,并绘制成如下统计图表.A款保温杯的保温时效统计表
保温时效小时
个数
11
6
12
1
13
6
14
7

请你根据以上信息解答下列问题:
(1)、将表格补充完整.保温时效
种类
平均数小时
中位数小时
众数小时
A款保温杯
13
B款保温杯
12.85
13
(2)、哪款保温杯的保温效果更好?请你结合所学的统计知识,简述理由.20. 如图,在的方格纸ABCD中,有一格点P,请按要求作图,且所画格点三角形与格点四边形的顶点均不与点A,B,C,D重合. (1)、在图1中画一个格点 , 使点Q,R分别落在边BC,CD上,且(2)、在图2中画一个有两边相等的格点四边形EFGH,使点E,F,G,H分别落在边AB,BC,CD,DA上,且点P在边EH上.21. 如图,已知A的坐标是 , 轴于点B,反比例函数的图象分别交AO,AB于点C,D,连接OD,的面积为2
(1)、在图1中画一个格点 , 使点Q,R分别落在边BC,CD上,且(2)、在图2中画一个有两边相等的格点四边形EFGH,使点E,F,G,H分别落在边AB,BC,CD,DA上,且点P在边EH上.21. 如图,已知A的坐标是 , 轴于点B,反比例函数的图象分别交AO,AB于点C,D,连接OD,的面积为2 (1)、求k的值和点C的坐标.(2)、若点在该反比例函数图象上,且在的内部包括边界 , 求b的取值范围.22. 如图,在四边形ABCD中,E为BC上一点, , , 且 , F是边AE上一点, , 连结
(1)、求k的值和点C的坐标.(2)、若点在该反比例函数图象上,且在的内部包括边界 , 求b的取值范围.22. 如图,在四边形ABCD中,E为BC上一点, , , 且 , F是边AE上一点, , 连结 (1)、求证:四边形ADCF是平行四边形.(2)、已知 , , 当时,求BC的长.23. 根据以下素材,探索完成任务.
(1)、求证:四边形ADCF是平行四边形.(2)、已知 , , 当时,求BC的长.23. 根据以下素材,探索完成任务.如何调整蔬菜大棚的结构?
素材1
我国的大棚如图种植技术已十分成熟,一块土地上有一个蔬菜大棚,其横截面顶部为抛物线型,大棚的一端固定在墙体OA上,另一端固定在墙体BC上,其横截面有2根支架DE,FG,相关数据如图2所示,其中支架 ,

素材2
已知大棚共有支架400根,为增加棚内空间,拟将图2中棚顶向上调整,支架总数不变,对应支架的长度变化如图3所示,调整后C与E上升相同的高度,增加的支架单价为60元/米接口忽略不计 , 现有改造经费32000元.

问题解决
任务1
确定大棚形状
在图2中建立合适的直角坐标系,求抛物线的函数表达式.
任务2
尝试改造方案
当米,只考虑经费情况下,请通过计算说明能否完成改造.
任务3
拟定最优方案
只考虑经费情况下,求出的最大值.
24. 如图1,在矩形OABC中, , 对角线AC,OB交于点D,E是AO延长线上一点,连结CE,DE,已知 , MN为半圆O的直径,CE切半圆O于点 (1)、求证:∽(2)、求半圆O的直径.(3)、如图2,动点P在CF上点C出发向终点F匀速运动,同时,动点Q从M出发向终点N匀速运动,且它们恰好同时停止运动.
(1)、求证:∽(2)、求半圆O的直径.(3)、如图2,动点P在CF上点C出发向终点F匀速运动,同时,动点Q从M出发向终点N匀速运动,且它们恰好同时停止运动.①当PQ与的一边平行时,求所有满足条件的MQ的长.
②作点F关于PQ的对称点 , 当点落在半圆O上时,直接写出的值.