浙江省宁波市宁海县北片2022-2023学年八年级下学期期中数学试卷

试卷更新日期：2023-05-06 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。）

1. 下列方程中，是一元二次方程的是（）

A、 $2 (x - 1) = x$ B、 $x^{2} - x y = 2$ C、 $x^{2} - 2 x + 1 = 0$ D、 $x^{2} + x = \frac{2}{x}$

查看试题解析
2. 要使 $\sqrt{x - 3}$ 有意义，则实数x的取值范围是（）

A、 $x \leq - 3$ B、 $x ≥ 3$ C、 $x \geq 0$ D、 $x \leq 0$

查看试题解析
3. 中国航天取得了举世瞩目的成就，为人类和平贡献了中国智慧和中国力量，下列是有关中国航天的图标，其文字上方的图案是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 若关于 $x$ 的方程 $x^{2} - 3 x + m = 0$ 有两个不相等的实数根，则 $m$ 的值可能是（）

A、5 B、2.5 C、 $\sqrt{10}$ D、-1

查看试题解析
5. 开学前，根据学校防疫要求，小宁同学连续14天进行了体温测量，结果统计如下表：
体温 $(℃)$
    36.2
    36.3
    36.5
    36.6
    36.8
天数 $($ 天 $)$
    3
    3
    4
    2
    2
这14天中，小宁体温的众数和中位数分别为（    ）

A、 $36.5 ℃$ ， $36.4 ℃$ B、 $36.5 ℃$ ， $36.5 ℃$ C、 $36.8 ℃$ ， $36.4 ℃$ D、 $36.8 ℃$ ， $36.5 ℃$

查看试题解析
6. 已知 $a$ 是方程 $x^{2} + 3 x + 2 = 0$ 的一个根，则代数式 $a^{2} + 3 a$ 的值为（）

A、-2 B、2 C、-4 D、-4或-10

查看试题解析
7. 下列各式中正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 $\sqrt{x^{2}} = x$ C、 $\sqrt[3]{(- x)^{3}} = - x$ D、 $\sqrt{(- x)^{2}} = - x$

查看试题解析
8. 为了迎接第二十二届世界杯足球赛，卡塔尔某地区举行了足球邀请赛，规定参赛的每两个队之间比赛一场，赛程计划安排7天，每天安排4场比赛 $.$ 设比赛组织者邀请了 $x$ 个队参赛，则下列方程正确的是（）

A、 $\frac{1}{2} x (x + 1) = 28$ B、 $x (x - 1) = 4$ C、 $x (x + 1) = 28$ D、 $\frac{1}{2} x (x - 1) = 28$

查看试题解析
9. 垦区小城镇建设如火如荼，小红家买了新楼．爸爸在正三角形、正方形、正五边形、正六边形四种瓷砖中，只购买一种瓷砖进行平铺，有几种购买方式（）

A、1种 B、2种 C、3种 D、4种

查看试题解析
10. 如图是一个由4张直角三角形纸片和1张正方形纸片拼成的平行四边形，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为 $S_{1} = 2$ ，则这个平行四边形的面积为（）

A、7 B、8 C、9 D、10

查看试题解析

二、填空题（本大题共6小题，共24.0分）

11. 化简二次根式 $\sqrt{\frac{4}{5}}$ 的结果为 .

查看试题解析
12. 去年某果园随机从甲、乙、丙、丁四个品种的葡萄树中各采摘了10棵，每棵产量的平均数 $\bar{x} ($ 单位：千克 $)$ 及方差 $s^{2}$ ，如表所示.今年准备从四个品种中选出一种产量既高又稳定的葡萄树进行种植，应选的品种是 $. ($ 填“甲”或“乙”或“丙”或“丁” $)$

甲
乙
丙
丁
$\bar{x}$
24
24
23
20
$S^{2}$
2.1
1.9
2
1.9

查看试题解析
13. 为解决看病难的问题，政府决定下调药品的价格，某种药品经过连续两次降价后，由每盒100元下调至64元，则这种药品平均每次降价的百分率是 .

查看试题解析
14. 如图，将一副三角板在平行四边形 $A B C D$ 中作如下摆放，设 $∠ 1 = 30 °$ ，那么 $∠ 2 =$ .

查看试题解析
15. 设 $x_{1}$ 、 $x_{2}$ 是方程 $x^{2} + m x - m + 3 = 0$ 的两个根，则 $x_{1} + x_{2} - x_{1} x_{2} =$ .

查看试题解析
16. 如图所示，已知平行四边形 $A B C D$ 的顶点 $A$ 的坐标为 $(0 ， \sqrt{10})$ ，顶点 $B$ ， $D$ 分别在 $x$ 轴和直线 $y = - 3$ 上，则对角线 $A C$ 的最小值是 .

查看试题解析

三、计算题（本大题共1小题，共8.0分）

17. 已知： $a = \sqrt{7} + 2$ ， $b = \sqrt{7} - 2$ ，求：

(1)、 $a b$ 的值；

(2)、 $a^{2} + b^{2} - 3 a b$ 的值；

(3)、若 $m$ 为 $a$ 整数部分， $n$ 为 $b$ 小数部分，求 $\frac{1}{m + n}$ 的值.

查看试题解析

四、解答题（本大题共7小题，共58.0分。）

18.

(1)、 $\sqrt{3} - 27 + | \sqrt{3} - 2 | - \sqrt{9} + (- 2)^{2}$ ；

(2)、 $\sqrt{40} - 5 \sqrt{\frac{1}{10}} - \sqrt{10}$ .

查看试题解析
19. 用适当的方法解下列方程.

(1)、 $x (x - 2) = 3 (2 - x)$ ；

(2)、 $2 x^{2} - 4 x + 1 = 0$ .

查看试题解析
20.
下列3×3网格图都是由9个相同的小正方形组成，每个网格图中有3个小正方形已涂上阴影，请在余下的6个空白小正方形中，按下列要求涂上阴影：

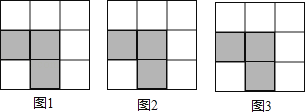(1)、选取1个涂上阴影，使4个阴影小正方形组成一个轴对称图形，但不是中心对称图形．

(2)、选取1个涂上阴影，使4个阴影小正方形组成一个中心对称图形，但不是轴对称图形．

(3)、选取2个涂上阴影，使5个阴影小正方形组成一个轴对称图形．
（请将三个小题依次作答在图1、图2、图3中，均只需画出符合条件的一种情形）

查看试题解析
21. 学校坚持“德育为先、智育为重、体育为基、美育为要、劳动为本”的五育并举育人理念，拟开展校级优秀学生评比活动 $.$ 下表是八年级1班三名同学综合素质考核的得分表： $($ 每项满分10分 $)$
姓名
行为规范
学习成绩
体育成绩
艺术获奖
劳动卫生
李铭
10
10
6
9
7
张晶晶
10
8
8
9
8
王浩
9
7
9
8
9

(1)、如果根据五项考核的平均成绩确定推荐1人，那么被推荐的是；

(2)、你认为表中五项考核成绩中最重要的是 ▲ ；请你设定一个各项考评内容的占分比例 $($ 比例的各项须满足： $①$ 均为整数； $②$ 总和为10； $③$ 不全相同 $)$ ，按这个比例对各项的得分重新计算，比较出大小关系，并从中推荐得分最高的作为校优秀学生的候选人.

查看试题解析
22. 为了落实劳动教育，某学校邀请农科院专家指导学生进行小番茄的种植，经过试验，其平均单株产量 $y$ 千克与每平方米种植的株数 $x$ 构成一种函数关系 $.$ 每平方米种植2株时，平均单株产量为4千克；以同样的栽培条件，每平方米种植的株数每增加1株，单株产量减少0.5千克.

(1)、求 $y$ 关于 $x$ 的函数表达式；

(2)、每平方米种植多少株时，能获得 $12.5 k g$ 的产量？

查看试题解析
23. 如图，在 $▱ A B C D$ 中，E是 $C D$ 的中点，连接 $A E$ 并延长交 $B C$ 的延长线于点F.

(1)、求证： $A E = F E$ ；

(2)、若 $D C = 2 B C$ ， $∠ F = 33 °$ .求 $∠ B A E$ 的度数.

查看试题解析
24. 在求解一类代数问题时，我们常常将二次三项式 $x^{2} + b x + c$ 化成 $(x + m)^{2} + n$ 的形式，并利用 $(x + m)^{2}$ 的非负性解决问题 $.$ 请阅读下列材料，并解决相关问题：
【例1】求代数式 $x^{2} + 4 x + 7$ 的最小值.
解： $x^{2} + 4 x + 7 = x^{2} + 4 x + 4 + 3 = (x + 2)^{2} + 3$ .
因为 $(x + 2)^{2} \geq 0$ ，所以 $(x + 2)^{2} + 3 \geq 3$ ，即代数式 $x^{2} + 4 x + 7$ 的最小值为3.
【例2】若 $m^{2} - 2 m n + 2 n^{2} - 8 n + 16 = 0$ ，求 $m$ 、 $n$ 的值.
解：因为 $m^{2} - 2 m n + 2 n^{2} - 8 n + 16 = 0$ ，
所以 $(m^{2} - 2 m n + n^{2}) + (n^{2} - 8 n + 16) = 0$ ，
即 $(m - n)^{2} + (n - 4)^{2} = 0$ ，
因为 $(m - n)^{2} \geq 0$ ， $(n - 4)^{2} \geq 0$ ，
所以 ${\begin{array}{l} m - n = 0 \\ n - 4 = 0 \end{array}$ ，
即 $m = n = 4$ .

(1)、求代数式 $x^{2} + 6 x + 10$ 的最小值；

(2)、在 $△ A B C$ 中， $B C = a$ ， $A C = b$ ， $A B = c$ .
$①$ 若 $△ A B C$ 是等腰三角形，且满足 $a^{2} - 8 a + b^{2} - 14 b + 65 = 0$ ，求 $△ A B C$ 的周长；
$②$ 若 $c - b = 1$ ，且 $c (b - 25) + 2 a^{2} - 20 a + 219 = 0$ ，求 $△ A B C$ 中最大边上的高.

查看试题解析

姓名	行为规范	学习成绩	体育成绩	艺术获奖	劳动卫生
李铭	10	10	6	9	7
张晶晶	10	8	8	9	8
王浩	9	7	9	8	9

体温 $(℃)$	36.2	36.3	36.5	36.6	36.8
天数 $($ 天 $)$	3	3	4	2	2

	甲	乙	丙	丁
$\bar{x}$	24	24	23	20
$S^{2}$	2.1	1.9	2	1.9