浙江省金华市金东区光南教育集团2022-2023学年七年级下学期月考数学试卷(3月份)
试卷更新日期:2023-05-06 类型:月考试卷
一、选择题(有10小题,每小题3分,共30分)
-
1. 如图,∠1和∠2是同位角的是( )A、
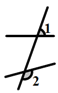 B、
B、 C、
C、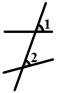 D、
D、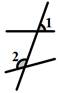 2. 下列是二元一次方程的是( )A、x-2= x B、4x+3y=1 C、x+ =0 D、2x-y=x23. 如图,“因为∠2=∠4,所以AD∥BC”,其推导的依据是( )
2. 下列是二元一次方程的是( )A、x-2= x B、4x+3y=1 C、x+ =0 D、2x-y=x23. 如图,“因为∠2=∠4,所以AD∥BC”,其推导的依据是( ) A、两直线平行,同位角相等 B、两直线平行,内错角相等 C、同位角相等,两直线平行 D、内错角相等,两直线平行4. 下列计算中,正确的是( )A、m2•m3=m5 B、(m3)2=m5 C、m+m2=2m3 D、(mn)3=mn35. 若 是方程2x+ay=3的解,则a的值为( )A、1 B、-1 C、7 D、-76. 若x2+kx-12=(x-6)(x+2),则k的值为( )A、8 B、-8 C、4 D、-47. 《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,余三;问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,多余3钱,问合伙人数、羊价各是多少?设合伙人数为x人,羊价为y钱,根据题意,可列方程组为( )A、 B、 C、 D、8. 对x,y定义一种新运算“※”,规定:x※y=mx+ny(其中m,n均为非零常数),若1※1=4,1※2=3.则2※1的值是( )A、3 B、5 C、9 D、119. 如图,生活中,将一个宽度相等的纸条按右图所示折叠一下,如果∠1=140°,那么∠2的度数为( )
A、两直线平行,同位角相等 B、两直线平行,内错角相等 C、同位角相等,两直线平行 D、内错角相等,两直线平行4. 下列计算中,正确的是( )A、m2•m3=m5 B、(m3)2=m5 C、m+m2=2m3 D、(mn)3=mn35. 若 是方程2x+ay=3的解,则a的值为( )A、1 B、-1 C、7 D、-76. 若x2+kx-12=(x-6)(x+2),则k的值为( )A、8 B、-8 C、4 D、-47. 《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,余三;问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,多余3钱,问合伙人数、羊价各是多少?设合伙人数为x人,羊价为y钱,根据题意,可列方程组为( )A、 B、 C、 D、8. 对x,y定义一种新运算“※”,规定:x※y=mx+ny(其中m,n均为非零常数),若1※1=4,1※2=3.则2※1的值是( )A、3 B、5 C、9 D、119. 如图,生活中,将一个宽度相等的纸条按右图所示折叠一下,如果∠1=140°,那么∠2的度数为( ) A、140° B、120° C、110° D、100°10. 如图,AB∥DE,BC⊥CD,则以下说法中正确的是( )
A、140° B、120° C、110° D、100°10. 如图,AB∥DE,BC⊥CD,则以下说法中正确的是( ) A、α,β的角度数之和为定值 B、α随β增大而增大 C、α,β的角度数之积为定值 D、α随β增大而减小
A、α,β的角度数之和为定值 B、α随β增大而增大 C、α,β的角度数之积为定值 D、α随β增大而减小二、填空题(有6小题,每小题4分,共24分).
-
11. 如图,直线a,b被直线c所截,并且a∥b,若∠1=108°,则∠2的度数是 .
 12. 已知方程2x-y=8,用含x的代数式表示y,则y=.13. 如图,△ABC沿BC所在直线向右平移得到△DEF,已知EC=4,BF=18,则平移的距离为 .
12. 已知方程2x-y=8,用含x的代数式表示y,则y=.13. 如图,△ABC沿BC所在直线向右平移得到△DEF,已知EC=4,BF=18,则平移的距离为 . 14. 已知 , ,则 的值为 .15. 如图,6块同样大小的小长方形刚好拼接成一个大长方形ABCD,已知AB=15cm,则每个小长方形的长为 cm.
14. 已知 , ,则 的值为 .15. 如图,6块同样大小的小长方形刚好拼接成一个大长方形ABCD,已知AB=15cm,则每个小长方形的长为 cm. 16. 一副直角三角板叠放如图①,∠C=∠E=90°.现将含45°角的三角板ADE固定不动,把含30°角的三角板ABC(其中∠CAB=30°)绕顶点A顺时针旋转角α(0°<α<180°).
16. 一副直角三角板叠放如图①,∠C=∠E=90°.现将含45°角的三角板ADE固定不动,把含30°角的三角板ABC(其中∠CAB=30°)绕顶点A顺时针旋转角α(0°<α<180°). (1)、如图②,当α=度时,边BC和边AE所在的直线互相垂直;(2)、当旋转角α在30°<α<180°的旋转过程中,使得两块三角板至少有一组对应边(所在的直线)互相平行,此时符合条件的α=.
(1)、如图②,当α=度时,边BC和边AE所在的直线互相垂直;(2)、当旋转角α在30°<α<180°的旋转过程中,使得两块三角板至少有一组对应边(所在的直线)互相平行,此时符合条件的α=.三、解答题(有8小题,共66分)
-
17. 计算:(1)、(3xy2)•(-2x3yz);(2)、(-3a3)2-3a•a5+(-2a2)3.18. 解方程组:(1)、 ;(2)、 .19. 先化简,后求值:(2a+b)(a-b)-a(a-2b),其中a=-2,b=3.20. 图①、图②均为5×5的正方形网格,每个小正方形的边长均为1个单位,△ABC的顶点均在格点上,根据下列条件,利用网格点和无刻度的直尺按要求作图并解答.
 (1)、在图①中过点B画线段AC的平行线BD.(2)、将△ABC向右上方平移,使点B平移到点B',
(1)、在图①中过点B画线段AC的平行线BD.(2)、将△ABC向右上方平移,使点B平移到点B',i.请在图②中画出经平移后得到的△A'B'C';
ii.在平移过程中,线段AB扫过的面积为 ▲ .
21. 如图,已知AD∥BC,点E在AB的延长线上,连结DE交BC于点F,且∠C=∠A. (1)、请说明∠E=∠CDE的理由;(2)、若∠1=75°,∠E=30°,求∠A的度数.22. 如图,长为y(cm),宽为x(cm)的大长方形被分割为7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短的边长为5cm.
(1)、请说明∠E=∠CDE的理由;(2)、若∠1=75°,∠E=30°,求∠A的度数.22. 如图,长为y(cm),宽为x(cm)的大长方形被分割为7小块,除阴影A,B外,其余5块是形状、大小完全相同的小长方形,其较短的边长为5cm. (1)、从图可知,每个小长方形的较长边的长是 cm(用含y的代数式表示).(2)、求阴影A和阴影B的周长和(用含x的代数式表示).(3)、当y=30时,用含x的代数式分别表示阴影A,B的面积,并比较A,B面积的大小.23. 某冬奥会纪念品专卖店计划同时购进“冰墩墩”和“雪容融”两种毛绒玩具.据了解,只“冰墩墩”和只“雪容融”的进价共计元;只“冰墩墩”和只“雪容融”的进价共计元.(1)、求“冰墩墩”和“雪容融”两种毛绒玩具每只进价分别是多少元.(2)、该专卖店计划恰好用元购进“冰墩墩”和“雪容融”两种毛绒玩具(两种均购买),求专卖店共有几种采购方案.(3)、若“冰墩墩”和“雪容融”两种毛绒玩具每只的售价分别是元,元,则在(2)的条件下,请选出利润最大的采购方案,并求出最大利润.24. 已知点C在射线OA上.
(1)、从图可知,每个小长方形的较长边的长是 cm(用含y的代数式表示).(2)、求阴影A和阴影B的周长和(用含x的代数式表示).(3)、当y=30时,用含x的代数式分别表示阴影A,B的面积,并比较A,B面积的大小.23. 某冬奥会纪念品专卖店计划同时购进“冰墩墩”和“雪容融”两种毛绒玩具.据了解,只“冰墩墩”和只“雪容融”的进价共计元;只“冰墩墩”和只“雪容融”的进价共计元.(1)、求“冰墩墩”和“雪容融”两种毛绒玩具每只进价分别是多少元.(2)、该专卖店计划恰好用元购进“冰墩墩”和“雪容融”两种毛绒玩具(两种均购买),求专卖店共有几种采购方案.(3)、若“冰墩墩”和“雪容融”两种毛绒玩具每只的售价分别是元,元,则在(2)的条件下,请选出利润最大的采购方案,并求出最大利润.24. 已知点C在射线OA上. (1)、如图①,CD∥OE,若∠AOB=90°,∠OCD=120°,求∠BOE的度数;(2)、在①中,将射线OE沿射线OB平移得O′E'(如图②),若∠AOB=α,探究∠OCD与∠BO′E′的关系(用含α的代数式表示);(3)、在②中,过点O′作OB的垂线,与∠OCD的平分线交于点P(如图③),若∠CPO′=90°,探究∠AOB与∠BO′E′的关系.
(1)、如图①,CD∥OE,若∠AOB=90°,∠OCD=120°,求∠BOE的度数;(2)、在①中,将射线OE沿射线OB平移得O′E'(如图②),若∠AOB=α,探究∠OCD与∠BO′E′的关系(用含α的代数式表示);(3)、在②中,过点O′作OB的垂线,与∠OCD的平分线交于点P(如图③),若∠CPO′=90°,探究∠AOB与∠BO′E′的关系.