浙江省杭州市北苑实验教育集团2022-2023学年八年级下学期期中数学试卷
试卷更新日期:2023-05-06 类型:期中考试
一、仔细选一选(本题有10个小题,每小题3分,共30分)
-
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 下列所给图形是中心对称图形但不是轴对称图形的是( )A、
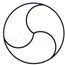 B、
B、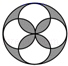 C、
C、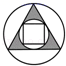 D、
D、 3. 已知m是方程x2-x-1=0的一个根,则代数式2m2-2m-3的值等于( )A、-2 B、0 C、-1 D、14. 小杭同学将自己前7次体育模拟测试成绩(单位一分)统计如表,第8次测试的成绩为a分,若这8次成绩的众数不止一个,则a的值为( )
3. 已知m是方程x2-x-1=0的一个根,则代数式2m2-2m-3的值等于( )A、-2 B、0 C、-1 D、14. 小杭同学将自己前7次体育模拟测试成绩(单位一分)统计如表,第8次测试的成绩为a分,若这8次成绩的众数不止一个,则a的值为( )次数
第1次
第2次
第3次
第4次
第5次
第6次
第7次
成绩
27
28
30
28
29
29
28
A、27 B、28 C、29 D、305. 已知平行四边形ABCD中,∠B=4∠A,则∠C=( )A、18° B、36° C、72° D、144°6. 为响应国家“双减政策”,某校2021年第三季度平均每周作业时长为600分钟,经过2021年第四季度和2022年第一季度两次整改后,平均每周作业时长为350分钟.设每季度平均每周作业时长的下降率为a,则可列方程为( )A、600(1-a)=350 B、350(1+a)=600 C、600(1-a)2=350 D、350(1+a)2=6007. 四边形的内角和等于 ,五边形的外角和等于 ,则下列关系成立的是( )A、 B、 C、 D、8. 已知平行四边形ABCD的对角线AC与BD相交于点O,BD⊥AC,若AB=6,AC=8,则对角线BD的长是( )A、2 B、2 C、4 D、49. 下列关于x的一元二次方程ax2+bx+c=0(a≠0)的命题中,真命题有( )①若a-b+c=0,则b2-4ac>0;②若方程ax2+bx+c=0(a≠0)两根为1和-2,则a-b=0;③若方程ax2+bx+c=0(a≠0)有一个根是-c(c≠0),则b=ac+1.
A、①②③ B、①② C、②③ D、①③10. 如图,▱ABCD的对角线AC,BD交于点O,AE平分∠BAD,交BC于点E,且∠ADC=60°,AB=BC,连接OE,下列结论:①∠CAD=30°;②OD=AB;③S▱ABCD=AC•CD;④S四边形OECD=S△AOD , 其中成立的个数为( )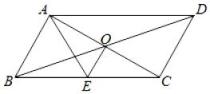 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、认真填一填(本题有6个小题,每小题4分,共24分)
-
11. 比较大小:﹣3 ﹣2 .12. 若关于x的一元二次方程x2-(m-2)x+4=0 有两个相等实数根,则m=.13. 已知一组数据1,5,2,4,x的平均数是3,则x=;这组数据的方差为 .14. 已知O是平行四边形两条对角线的交点, , , , 则的周长为.15. 已知(m-3)≤0.若整数a满足m+a=5 , 则a=.16. 如图,在Rt△ABC中,∠ACB=90°,以斜边AB为边向下做正方形ADEB,过点E作EF∥BC交AC于点F,过点C作CG∥BE交EF于点G,连接DG,若AF=3,DE=15,则线段AD与CG的数量关系是 ;四边形CGEB的面积为 .

三、全题答一答(本题有7个小题,分值为6+8+8+10+10+12+12,共66分)
-
17. 计算:(1)、(3)+;(2)、.18. 解方程:(1)、x2-x=0;(2)、.19. 弘扬中华传统文化,感受中华诗词的独特魅力,校团委会举办首届“校园诗词大会”,初赛共10道题,每题10分,王敏从初赛名单中随机抽取部分同学的成绩,绘制出如下的统计图(1)和图(2).请根据相关信息,解答下列问题:
 (1)、图(1)a的值为▲ , 补全条形统计图;(2)、求被抽取的初赛成绩的平均数,众数和中位数;(3)、如果初赛成绩在90分或90分以上的同学进入复赛,请估计参加初赛的200位同学中有多少同学可以参加复赛.20. 如图,▱ABCD的对角线AC,BD相交于点O,E,F分别是OB,OD的中点,连接AE,AF,CE,CF.
(1)、图(1)a的值为▲ , 补全条形统计图;(2)、求被抽取的初赛成绩的平均数,众数和中位数;(3)、如果初赛成绩在90分或90分以上的同学进入复赛,请估计参加初赛的200位同学中有多少同学可以参加复赛.20. 如图,▱ABCD的对角线AC,BD相交于点O,E,F分别是OB,OD的中点,连接AE,AF,CE,CF.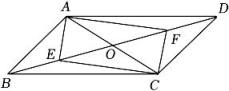 (1)、求证:四边形AECF是平行四边形;(2)、若AB⊥AC,AB=3,BC=5.
(1)、求证:四边形AECF是平行四边形;(2)、若AB⊥AC,AB=3,BC=5.①求AC的长;
②求BD的长.
21. 作图: (1)、直接写出AC的长为 .(2)、在图1中找到格点D,画出以点A、B、C、D为顶点的平行四边形,画出所有的情况的平行四边形.(3)、在图2中找到格点D,画出以点A、B、C、D为顶点且周长最小的平行四边形,直接写出周长最小值.(4)、在(3)条件下,直接写出平行四边形的面积.22. 对于向上抛的物体,如果空气阻力忽略不计,有下面的关系式:h=v0t-gt2(h是物体离起点的高度,v0是初速度,g是重力系数,取10m/s2 , t是抛出后经过的时间).杂技演员抛球表演时,以10m/s的初速度把球向上抛出,球的起点离开地面2m.(1)、1.2秒时球离起点的高度是多少?(2)、几秒后球离起点的高度达到2.55m?(3)、球经过多少时间才落地?23. 如图1,Rt△ABC中,∠ACB=90,BC=4,∠ABC=60°,点P、Q是边AB,BC上两个动点,且BP=4CQ,以BP,BQ为邻边作平行四边形BPDQ,PD,QD分别交AC于点E,F,设CQ=m.
(1)、直接写出AC的长为 .(2)、在图1中找到格点D,画出以点A、B、C、D为顶点的平行四边形,画出所有的情况的平行四边形.(3)、在图2中找到格点D,画出以点A、B、C、D为顶点且周长最小的平行四边形,直接写出周长最小值.(4)、在(3)条件下,直接写出平行四边形的面积.22. 对于向上抛的物体,如果空气阻力忽略不计,有下面的关系式:h=v0t-gt2(h是物体离起点的高度,v0是初速度,g是重力系数,取10m/s2 , t是抛出后经过的时间).杂技演员抛球表演时,以10m/s的初速度把球向上抛出,球的起点离开地面2m.(1)、1.2秒时球离起点的高度是多少?(2)、几秒后球离起点的高度达到2.55m?(3)、球经过多少时间才落地?23. 如图1,Rt△ABC中,∠ACB=90,BC=4,∠ABC=60°,点P、Q是边AB,BC上两个动点,且BP=4CQ,以BP,BQ为邻边作平行四边形BPDQ,PD,QD分别交AC于点E,F,设CQ=m.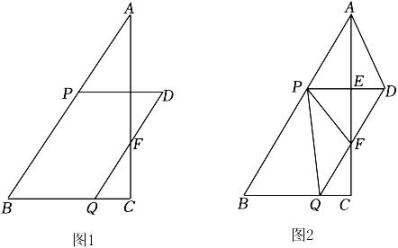 (1)、直接写出BQ=;CE=.(用含m的代数式表示)(2)、当平行四边形BPDQ的面积为6时,求m的值;(3)、求证:△DEF≌△QCF;(4)、如图2,连接AD,PF,PQ,当AD与△PQF的一边平行时,求△PQF的面积.
(1)、直接写出BQ=;CE=.(用含m的代数式表示)(2)、当平行四边形BPDQ的面积为6时,求m的值;(3)、求证:△DEF≌△QCF;(4)、如图2,连接AD,PF,PQ,当AD与△PQF的一边平行时,求△PQF的面积.