人教版初中数学几何辅助线进阶训练——正方形的辅助线（不含相似）
试卷更新日期：2023-05-06 类型：复习试卷
一、阶段一（较易）
-
1.
感知：如图①，在正方形ABCD中，点E在对角线AC上（不与点A、C重合），连结ED，EB，过点E作EF⊥ED，交边BC于点F.易知∠EFC+∠EDC=180°，进而证出EB=EF.
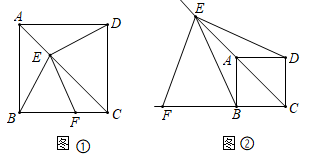(1)、探究：如图②，点E在射线CA上（不与点A、C重合），连结ED、EB，过点E作EF⊥ED，交CB的延长线于点F.求证：EB=EF.(2)、应用：如图②，若DE=2，CD=1，则四边形EFCD的面积为.2.(1)、【阅读理解】如图1， ， 的面积与的面积相等吗？为什么？
(2)、【类比探究】问题①，如图2，在正方形的右侧作等腰 ， ， ， 连接 ， 求的面积.
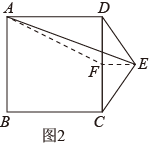(3)、【拓展应用】问题②，如图3，在正方形的右侧作正方形 ， 点B，C，E在同一直线上， ， 连接 ， ， ， 直接写出的面积.
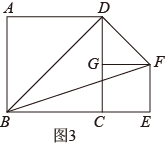3. 如图，在正方形ABCD中，AB=8，F是对角线AC的中点，点G、E分别在AD、CD边上运动，且保持AG=DE．连接GE、GF、EF．在此运动变化的过程中，下列结论：①△GFE是等腰直角三角形；②四边形DGFE不可能为正方形，③GE长度的最小值为4；④四边形DGFE的面积保持不变；⑤△DGE面积的最大值为8．其中正确的结论是（ ）
A、①②③ B、①③④⑤ C、①③④ D、③④⑤4. 综合与实践小明遇到这样一个问题，如图1，中， ， ， 点D为的中点，求的取值范围.
小明发现老师讲过的“倍长中线法”可以解决这个问题，所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法，他的做法是：如图2，延长到E，使 ， 连接 ， 构造 ， 经过推理和计算使问题得到解决
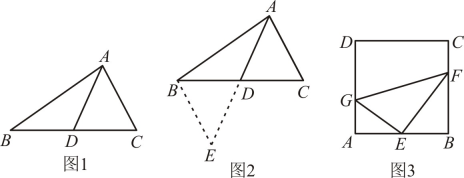
请回答：
(1)、小明证明用到的判定定理是：____；（填入你选择的选项字母）A、 B、 C、 D、(2)、的取值范围是.(3)、小明还发现：倍长中线法最重要的一点就是延长中线一倍，完成全等三角形模型的构造.
参考小明思考问题的方法，解决问题：
如图3，在正方形中，E为边的中点，G、F分别为 ， 边上的点，若 ， ， ， 求的长.5. 如图，正方形中，点在上，连接 ， 点在上，连接 ， ， ， ， 则的长为 ．
6. 如图，点E和W分别在正方形边上，和交于F，过B作于H，若 ， ， 则线段的长为 ．
7. 如图，在四边形中， ， ， ， 连接 ， 则等于 ．
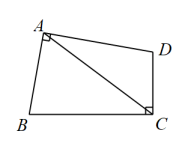8. 如图1，把一个含角的直角三角板和一个正方形摆放在一起，使三角板的直角顶点和正方形的顶点重合，点、分别在正方形的边、上，连接 ， 取中点 ， 的中点 ， 连接、.
(1)、如图1，连接 ， 求证：；(2)、在（1）的条件下，请判断线段与之间的数量关系，并加以证明；(3)、如图2，将这个含角的直角三角板的直角顶点和正方形的顶点重合，点、分别在正方形的边、的延长线上，其他条件不变，当 ， 时，求的长.9. 已知正方形的周长为16.E在边上运动，的中点G，绕E顺时针旋转90°得到.当A，C，F在同一条直线上，则的长为（ ）
A、 B、 C、 D、10. 如图，已知四边形是正方形， ， 点E为对角线上一动点，连接 ， 过点E作 ， 交射线于点F，以 ， 为邻边作矩形 ， 连接 ．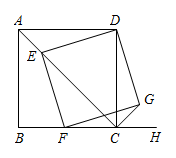
(1)、；(2)、若四边形的面积为5，则二、阶段二（一般）
-
11. 如图，在正方形中，点E在边上，连接 ， 的垂直平分线交于点M，交于点N，连接 ， 过点E作的垂线交于点F，连接 ． 下列结论：①；②平分；③；④的周长等于 ． 其中结论正确的序号有（ ）
A、①②③ B、②③④ C、①④ D、①②③④12. 如图，E是正方形边上一点，连接平分交于点F．过F作 ， 垂足为G，连接并延长交延长线于点H，若 ， 则 ．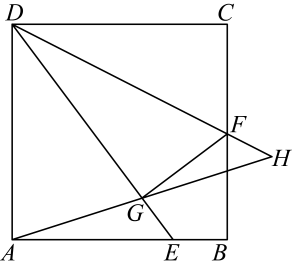
13. 已知四边形是正方形，点为射线上一点，连接并以为对角线作正方形 ， 连接 ， ．
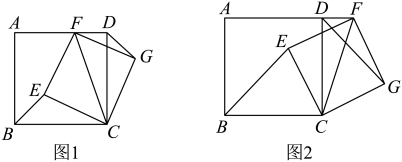(1)、如图 ， 当点在线段上时，求证：；(2)、如图 ， 当点在线段上时，求证：；(3)、如图 ， 当点在线段的延长线上时，请直接写出线段 ， 与间满足的关系式．14. 如图，小王同学用图1的一副七巧板拼出如图2所示的“雄鹰”.已知正方形的对角线的长为 ， 则图2中E、F两点之间的距离为.
15. 阅读下面材料.小炎遇到这个一个问题：如图1，点E、F分别在正方形的边上， ， 连接 ， 则 ， 试说明理由.
小炎是这样思考的：要想解决这个问题，首先应想办法将这些分散的线段相对集中，她先尝试了翻折、旋转、平移的方法，最后发现线段是共点并且相等的，于是找到解决问题的方法.她的方法是将绕着点A逆时针旋转90°得到 ， 再利用全等的知识解决这个问题（如图2）.
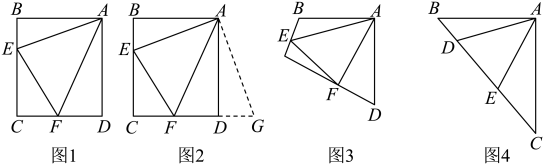
参考小炎同学思考问题的方法，解决下列问题：
(1)、写出小炎的推理过程；(2)、如图3，四边形ABCD中， ， ， 点E、F分别在边上， ， 若、都不是直角，则当与满足于关系时，仍有；(3)、如图4，在中， ， ， 点D、E均在边BC上，且 ， 若 ， ， 求DE的长.16. 如图，已知正方形的边长为1，点M是边的中点，将沿直线翻折，使得点C落在同一平面内的点E处，联结并延长交射线于点F，那么的长为 ．
17. 综合与实践问题情境：数学活动课上，老师提出如下问题：如图1，在正方形中，是对角线上一点，将直线以点为中心逆时针旋转 ， 旋转后的直线与交于点 ． 求证： ．
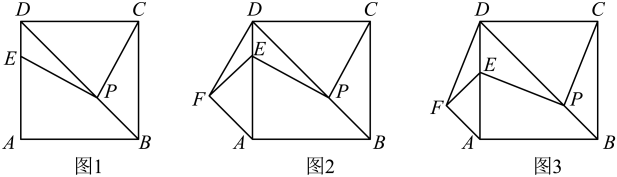(1)、问题解决：请你解决老师提出的问题；
(2)、数学思考：如图2，“兴趣小组”的同学将沿射线的方向平移到 ， 点的对应点为 ． 连接 ． 他们认为： ， ． 他们的认识是否正确？请说明理由．
(3)、创新探究“创新小组”在“兴趣小组”所提问题的基础上，又提出如下新问题，请你思考并解决该问题：如图3，若垂直平分 ， ， 则线段的长度是 ． （直接写出答案即可）
18. 如图，正方形的边长为 ， ， ， 连结 ， 则线段的长为（ ）
A、 B、 C、 D、19. 如图，在边长为6的正方形ABCD内作∠EAF＝45°，AE交BC于点E，AF交CD于点F，连接EF．若DF＝3，则BE的长为（ ）
A、2 B、3 C、4 D、520. 如图，在正方形中， ， E，F分别为边的中点，连接 ， 点G，H分别为的中点，连接 ， 则的长为（ ）
A、 B、1 C、 D、2三、阶段三（较难）
-
21. 如图，在正方形ABCD中，G是对角线BD上的点，GE⊥CD，GF⊥BC，E，F分别为垂足，连结EF．设M，N分别是AB，BG的中点，EF＝5，求MN的长．
22. 如图1，已知正方形ABCD的边CD在正方形DEFG的边DE上，连接AE，GC．
(1)、试猜想AE与GC有怎样的位置关系，并证明你的结论；(2)、将正方形DEFG绕点D按顺时针方向旋转，使点E落在BC边上，如图2，连接AE和GC．你认为（1）中的结论是否还成立？若成立，给出证明；若不成立，请说明理由．23.提出问题：如图1，将三角板放在正方形ABCD上，使三角板的直角顶点P在对角线AC上，一条直角边经过点B，另一条直角边交边DC于点E，求证：PB=PE
分析问题：学生甲：如图1，过点P作PM⊥BC，PN⊥CD，垂足分别为M，N通过证明两三角形全等，进而证明两条线段相等．
学生乙：连接DP，如图2，很容易证明PD=PB，然后再通过“等角对等边”证明PE=PD，就可以证明PB=PE了．
解决问题：请你选择上述一种方法给予证明．
问题延伸：如图3，移动三角板，使三角板的直角顶点P在对角线AC上，一条直角边经过点B，另一条直角边交DC的延长线于点E，PB=PE还成立吗？若成立，请证明；若不成立，请说明理由．
24. 如图，已知正方形ABCD，∠MAN＝45°，连接CB，交AM、AN分别于点P、Q，求证：CP2+BQ2＝PQ2.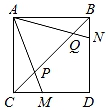
25. 已知：如图，正方形 ， 、 分别平分正方形的两个外角，且满足 ，连接 ．若以 ， ， 为三边围成三角形，试猜想该三角形的形状，并证明你的结论．
26. 如图，四边形ABCD是正方形，点E在直线BC上，连接AE．将△ABE沿AE所在直线折叠，点B的对应点是点B′，连接AB′并延长交直线DC于点F．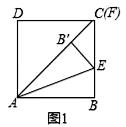
(1)、当点F与点C重合时如图1，证明：DF+BE=AF；(2)、当点F在DC的延长线上时如图2，当点F在CD的延长线上时如图3，线段DF、BE、AF有怎样的数量关系？请直接写出你的猜想，并选择一种情况给予证明．
27. 如图，点G是正方形ABCD对角线CA的延长线上任意一点，以线段AG为边作一个正方形AEFG，线段EB和GD相交于点H．
(1)、求证：EB=GD；(2)、判断EB与GD的位置关系，并说明理由；(3)、若AB=2，AG= ，求EB的长．28.四边形ABCD是正方形，AC与BD，相交于点O，点E、F是直线AD上两动点，且AE=DF，CF所在直线与对角线BD所在直线交于点G，连接AG，直线AG交BE于点H．
（1）如图1，当点E、F在线段AD上时，①求证：∠DAG=∠DCG；②猜想AG与BE的位置关系，并加以证明；
（2）如图2，在（1）条件下，连接HO，试说明HO平分∠BHG；
（3）当点E、F运动到如图3所示的位置时，其它条件不变，请将图形补充完整，并直接写出∠BHO的度数．
29.阅读下面材料：
小明遇到这样一个问题：如图1，在边长为的正方形ABCD各边上分别截取AE=BF=CG=DH=1，当∠AFQ=∠BGM=∠CHN=∠DEP=45°时，求正方形MNPQ的面积.小明发现：分别延长QE，MF，NG，PH，交FA，GB，HC，ED的延长线于点R，S，T，W，可得△RQF，△SMG，△TNH，△WPE是四个全等的等腰直角三角形（如图2）
请回答：
（1）若将上述四个等腰直角三角形拼成一个新的正方形（无缝隙，不重叠），则这个新的正方形的边长为__________；
（2）求正方形MNPQ的面积.
参考小明思考问题的方法，解决问题：
如图3，在等边△ABC各边上分别截取AD=BE=CF，再分别过点D，E，F作BC，AC，AB的垂线，得到等边△RPQ，若 ， 则AD的长为__________.
30.(1)如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE.求证：CE＝CF；
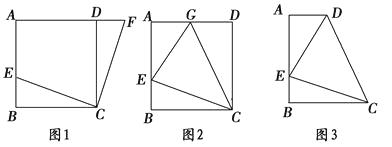
(2)如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE＝45°，请你利用(1)的结论证明：GE＝BE＋GD；
(3)运用(1)(2)解答中所积累的经验和知识，完成下题：
如图3，在直角梯形ABCD中，AD∥BC，(BC>AD)，∠B＝90°，AB＝BC，E是AB上一点，且∠DCE＝45°，BE＝4，DE＝10，求直角梯形ABCD的面积．