上海市杨浦区2023年中考二模数学试卷
试卷更新日期:2023-05-05 类型:中考模拟
一、单选题
-
1. 下列单项式中,xy2的同类项是( )A、x3y2 B、x2y C、2xy2 D、2x2y32. 下列正确的是()A、 B、 C、 D、3. 下列检测中,适宜采用普查方式的是( )A、检测一批充电宝的使用寿命 B、检测一批电灯的使用寿命 C、检测一批家用汽车的抗撞击能力 D、检测“神舟十六号”载人飞船零件的质量4. 下列函数中,函数值 随自变量 的值增大而增大的是( )A、 B、 C、 D、5. 已知两圆相交,它们的圆心距为3,一个圆的半径是2,那么另一个圆的半径长可以是( )A、1 B、3 C、5 D、76. 下列命题中,正确的是( )A、对角线相等的四边形是平行四边形 B、对角线互相垂直的四边形是菱形 C、对角线相等的平行四边形是矩形 D、对角线互相垂直且相等的四边形是正方形
二、填空题
-
7. ﹣(﹣2)= .8. 分解因式: = .9. 方程 的根是 .10. 掷一枚材质均匀的骰子,掷得的点数为素数的概率是 .11. 如果抛物线的顶点是它的最高点,那么a的取值范围是 .12. 如果关于x的二次三项式在实数范围内不能因式分解,那么k的取值范围是 .13. 在中,点D是的中点, , , 那么 .(用、表示).14. 某校初三(1)班40名同学的体育成绩如表所示,则这40名同学成绩的中位数是 .
成绩(分)
25
26
27
28
29
30
人数
2
5
6
8
12
7
15. 《孙子算经》中记载:“凡大数之法,万万曰亿,万万亿曰兆.”说明了大数之间的关系:1亿=1万×1万,1兆=1万×1万×1亿,那么2兆= . (用科学记数法表示)16. 如图,某地下停车库入口的设计示意图,已知 , 坡道AB的坡比 , 的长为7.2米,的长为0.4米.按规定,车库坡道口上方需张贴限高标志,以便告知停车人车辆是否能安全驶入,根据所给数据,确定该车库入口的限高,即点D到AB的距离的值为米. 17. 如图,正五边形形ABCDE的边长为2,分别以点C、D为圆心,CD长为半径画弧,两弧交于点F,则的长为 . (结果保留)
17. 如图,正五边形形ABCDE的边长为2,分别以点C、D为圆心,CD长为半径画弧,两弧交于点F,则的长为 . (结果保留) 18. 如图,已知在扇形AOB中,∠AOB=60°,半径OA=8,点P在弧AB上,过点P作PC⊥OA于点C,PD⊥OB于点D,那么线段CD的长为 .
18. 如图,已知在扇形AOB中,∠AOB=60°,半径OA=8,点P在弧AB上,过点P作PC⊥OA于点C,PD⊥OB于点D,那么线段CD的长为 .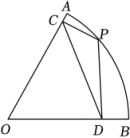
三、解答题
-
19. 先化简再求值: , 其中 .20. 解不等式组 , 并求出它的正整数解.21. 已知一次函数的图象与反比例函数的图象相交于点 , .
 (1)、求一次函数的解析式;(2)、过点A作直线 , 交y轴于点D,交第三象限内的反比例函数图象于点C,连接 , 如果 , 求线段的长.22. 如图,某水渠的横断面是以为直径的半圆O,其中水面截线 , 小明在A处测得点B处小树的顶端C的仰角为 , 已知小树的高为米.
(1)、求一次函数的解析式;(2)、过点A作直线 , 交y轴于点D,交第三象限内的反比例函数图象于点C,连接 , 如果 , 求线段的长.22. 如图,某水渠的横断面是以为直径的半圆O,其中水面截线 , 小明在A处测得点B处小树的顶端C的仰角为 , 已知小树的高为米. (1)、求直径的长;(2)、如果要使最大水深为2.8米,那么此时水面的宽度约为多少米.(结果精确到0.1米,参考数据: , )23. 已知:在直角梯形中, , , 沿直线翻折,点A恰好落在腰上的点E处.
(1)、求直径的长;(2)、如果要使最大水深为2.8米,那么此时水面的宽度约为多少米.(结果精确到0.1米,参考数据: , )23. 已知:在直角梯形中, , , 沿直线翻折,点A恰好落在腰上的点E处.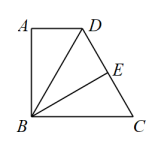 (1)、如图,当点E是腰的中点时,求证:是等边三角形;(2)、延长交线段的延长线于点F,连接 , 如果 , 求证:四边形是矩形.
(1)、如图,当点E是腰的中点时,求证:是等边三角形;(2)、延长交线段的延长线于点F,连接 , 如果 , 求证:四边形是矩形.

