上海市闵行区2023年中考二模数学试题
试卷更新日期:2023-05-05 类型:中考模拟
一、单选题
-
1. 单项式的次数是( )A、1 B、2 C、3 D、42. 上海某区3月20日至3月26日的气温()如下表:
日期
20日
21日
22日
23日
24日
25日
26日
天气
多云
晴
晴
阴
多云
阴
小雨
最低气温
12
15
11
8
9
8
8
最高气温
16
22
23
13
15
13
13
那么这一周最高气温的众数和中位数分别是( )
A、13,13; B、13,15; C、8,15; D、8,13.3. 一次函数的图像经过第一、二、三象限,它的解析式可以是( )A、 B、 C、 D、4. 下列命题是真命题的是( )A、平行四边形的邻边相等; B、平行四边形的对角线互相平分; C、平行四边形内角都相等; D、平行四边形是轴对称图形.5. 在平面直角坐标系中,如果把抛物线向下平移3个单位得到一条新抛物线,那么下列关于这两条抛物线的描述中错误的是( )A、开口方向相同; B、对称轴相同; C、顶点的横坐标相同; D、顶点的纵坐标相同.6. 如图,在中, . 用尺规作图的方法作出直角三角形斜边上的中线 , 那么下列作法一定正确的是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
7. 计算:2a+3a= .8. 因式分解: .9. 已知关于的方程有两个相等的实数根,那么的值为 .10. 方程的根是 .11. 如图,已知梯形ABCD,AD∥BC,BC=2AD,如果 , , 那么=(用 , 表示).
 12. 2022年10月12日,“天宫课堂”第三课在问天实验舱内开讲.进行的太空实验有①毛细效应;②水球变“懒”实验;③太空趣味饮水;④会调头的扳手.某校1500名学生在线观看了“天宫课堂”第三课,并参与了关于“我最喜爱的太空实验”的问卷调查.如果从中随机抽取45名学生的问卷调查情况进行统计分析,并将调查数据整理成下面的条形图,那么估计该校喜欢③太空趣味饮水实验的初中学生有名.
12. 2022年10月12日,“天宫课堂”第三课在问天实验舱内开讲.进行的太空实验有①毛细效应;②水球变“懒”实验;③太空趣味饮水;④会调头的扳手.某校1500名学生在线观看了“天宫课堂”第三课,并参与了关于“我最喜爱的太空实验”的问卷调查.如果从中随机抽取45名学生的问卷调查情况进行统计分析,并将调查数据整理成下面的条形图,那么估计该校喜欢③太空趣味饮水实验的初中学生有名.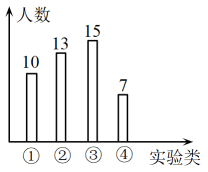 13. 为开展“学习二十大,奋进新征程”主题宣讲活动,某学校从甲、乙、丙三位宣讲员中随机抽取两人参加,恰好选中甲、丙两人的概率为 .14. 如果正六边形的半径长为2,那么它的面积为 .15. 我国古代数学名著《张丘建算经》中记载:“今有清酒一斗直粟十斗,醐洒一斗直粟三斗,今持粟三斛,得酒五斗,问清跴酒各几何?”大意是:现有一斗清酒价值10斗谷子,一斗醐洒酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清洒,醐洒酒各几斗?如果设清酒x斗,那么可列方程为 .16. 如图,在平面直角坐标系中,点A在直线上,点A的横坐标为1,点P是x轴正半轴上一点,点B在反比例函数图象上,联结和 . 如果四边形是矩形,那么k的值是 .
13. 为开展“学习二十大,奋进新征程”主题宣讲活动,某学校从甲、乙、丙三位宣讲员中随机抽取两人参加,恰好选中甲、丙两人的概率为 .14. 如果正六边形的半径长为2,那么它的面积为 .15. 我国古代数学名著《张丘建算经》中记载:“今有清酒一斗直粟十斗,醐洒一斗直粟三斗,今持粟三斛,得酒五斗,问清跴酒各几何?”大意是:现有一斗清酒价值10斗谷子,一斗醐洒酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清洒,醐洒酒各几斗?如果设清酒x斗,那么可列方程为 .16. 如图,在平面直角坐标系中,点A在直线上,点A的横坐标为1,点P是x轴正半轴上一点,点B在反比例函数图象上,联结和 . 如果四边形是矩形,那么k的值是 .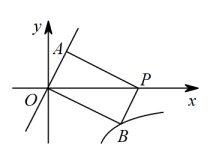 17. 如图,在菱形中, , , 如果将菱形绕着点D逆时针旋转后,点A恰好落在菱形的初始边上的点E处,那么点E到直线的距离为 .
17. 如图,在菱形中, , , 如果将菱形绕着点D逆时针旋转后,点A恰好落在菱形的初始边上的点E处,那么点E到直线的距离为 . 18. 阅读理解:如果一个三角形中有两个内角、满足 , 那么我们称这个三角形为特征三角形.
18. 阅读理解:如果一个三角形中有两个内角、满足 , 那么我们称这个三角形为特征三角形.问题解决:如图,在中,为钝角, , , 如果是特征三角形,那么线段的长为 .

三、解答题
-
19. 计算:20. 解不等式组 , 并把解集在数轴上表示出来;
 21. 如图,在中, , , , 点D为的中点,过点B作CD的垂线,交CD的延长线于点E.
21. 如图,在中, , , , 点D为的中点,过点B作CD的垂线,交CD的延长线于点E. (1)、求线段的长;(2)、求的值.22. 如图,在修建公路时,需要挖掘一段隧道 , 已知点A、B、C、D在同一直线上, , , 米;
(1)、求线段的长;(2)、求的值.22. 如图,在修建公路时,需要挖掘一段隧道 , 已知点A、B、C、D在同一直线上, , , 米; (1)、求隧道两端B、C之间的距离(精确到个位);
(1)、求隧道两端B、C之间的距离(精确到个位);(参考数据: , , ).
(2)、原计划单向开挖,但为了加快施工进度,从B、C两端同时相向开挖,这样每天的工作效率提高了20%,结果提前2天完工.问原计划单向开挖每天挖多少米?23. 如图,在扇形中,点C、D在上, , 点F、E分别在半径、上, , 连接、 . (1)、求证:;(2)、设点Р为的中点,连接、、 , 线段交于点M、交于点N.如果 , 求证:四边形是矩形.
(1)、求证:;(2)、设点Р为的中点,连接、、 , 线段交于点M、交于点N.如果 , 求证:四边形是矩形.