山东省淄博市临淄区2023年中考一模数学试题
试卷更新日期:2023-05-05 类型:中考模拟
一、选择题
-
1. 如图,几何体的左视图是( ).
 A、
A、 B、
B、 C、
C、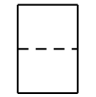 D、
D、 2. 已知1米纳米.某种病毒的直径为125纳米,“125纳米”用科学记数法可以表示为( ).A、米 B、米 C、米 D、米3. 如图是某班去年1~8月份全班同学每月的课外阅读数量折线计图,下列说法正确的是( )
2. 已知1米纳米.某种病毒的直径为125纳米,“125纳米”用科学记数法可以表示为( ).A、米 B、米 C、米 D、米3. 如图是某班去年1~8月份全班同学每月的课外阅读数量折线计图,下列说法正确的是( ) A、每月阅读数量的众数是83 B、每月阅读数量的中位数是58 C、每月阅读数量的平均数是50 D、每月阅读数量的极差是654. 如图,衣架可以近似看成一个等腰三角形 , 其中 , , , 则高约为( ).(参考数据: , , )
A、每月阅读数量的众数是83 B、每月阅读数量的中位数是58 C、每月阅读数量的平均数是50 D、每月阅读数量的极差是654. 如图,衣架可以近似看成一个等腰三角形 , 其中 , , , 则高约为( ).(参考数据: , , )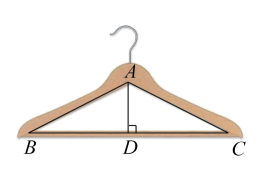 A、 B、 C、 D、5. 下列各式运算正确的是( ).A、 B、 C、 D、6. 如图所示,若用我们数学课本上采用的科学计算器进行计算,其按键顺序如下:
A、 B、 C、 D、5. 下列各式运算正确的是( ).A、 B、 C、 D、6. 如图所示,若用我们数学课本上采用的科学计算器进行计算,其按键顺序如下:按键
 的结果为m,
的结果为m,按键
 的结果为n,则下列判断正确的是( )A、 B、 C、 D、无法确定7. 如图,在中, , , 通过观察尺规作图的痕迹,的度数是( ).
的结果为n,则下列判断正确的是( )A、 B、 C、 D、无法确定7. 如图,在中, , , 通过观察尺规作图的痕迹,的度数是( ). A、 B、 C、 D、8. 如图,日晷是中国古代用来测定时间的仪器,利用与晷盘垂直的晷针投射到晷盘上的影子来测定时间.淄博市某学校内A处有一个日晷模型,晷盘与赤道面平行,平面示意图如下,A处的纬度为北纬(地球球心为O,A处的纬度是指与赤道面所成角),则晷针与底座所成角为( ).
A、 B、 C、 D、8. 如图,日晷是中国古代用来测定时间的仪器,利用与晷盘垂直的晷针投射到晷盘上的影子来测定时间.淄博市某学校内A处有一个日晷模型,晷盘与赤道面平行,平面示意图如下,A处的纬度为北纬(地球球心为O,A处的纬度是指与赤道面所成角),则晷针与底座所成角为( ).
 A、 B、 C、 D、9. 已知关于x的方程的两实数根为 , , 则m的值为( )A、﹣3 B、﹣1 C、﹣3或1 D、﹣1或310. 如图,中, , , 边上的高 , 点 , , 分别在边 , , 上,且四边形为正方形,点 , , 分别在边1, , 上,且四边形为正方形,…按此规律操作下去,则线段的长度为( ).
A、 B、 C、 D、9. 已知关于x的方程的两实数根为 , , 则m的值为( )A、﹣3 B、﹣1 C、﹣3或1 D、﹣1或310. 如图,中, , , 边上的高 , 点 , , 分别在边 , , 上,且四边形为正方形,点 , , 分别在边1, , 上,且四边形为正方形,…按此规律操作下去,则线段的长度为( ). A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 在函数中,自变量x的取值范围是 .12. 分解因式:x2﹣5x+6= .13. 如图,菱形中,分别以点 , 为圆心, , 长为半径画弧,分别交对角线于点 , . 若 , , 则图中阴影部分的面积为 . (结果不取近似值)
 14. 如图,点A、B、C三点分别在反比例函数y= (x<0)、y= (x>0)、y= (x>0)的图象上,AC⊥y轴于点E,BC⊥x轴于点F,AB经过原点,若S△ABC=5,则k1+k2-2k3的值为.
14. 如图,点A、B、C三点分别在反比例函数y= (x<0)、y= (x>0)、y= (x>0)的图象上,AC⊥y轴于点E,BC⊥x轴于点F,AB经过原点,若S△ABC=5,则k1+k2-2k3的值为. 15. 华罗庚说过:“复杂的问题要善于‘退’,足够地‘退’,‘退’到最原始而不失重要性的地方,是学好数学的一个诀窍.”可见,复杂的问题有时要“退”到本质上去研究.如图,已知抛物线的图象与f的图象关于直线对称,我们把探索线的变化规律“退”到探索点的变化规律上去研究,可以得到图象f所对应的关于x与y的关系式为 . 若抛物线与g的图象关于对称,则图象g所对应的关于x与y的关系式为 .
15. 华罗庚说过:“复杂的问题要善于‘退’,足够地‘退’,‘退’到最原始而不失重要性的地方,是学好数学的一个诀窍.”可见,复杂的问题有时要“退”到本质上去研究.如图,已知抛物线的图象与f的图象关于直线对称,我们把探索线的变化规律“退”到探索点的变化规律上去研究,可以得到图象f所对应的关于x与y的关系式为 . 若抛物线与g的图象关于对称,则图象g所对应的关于x与y的关系式为 .
三、解答题
-
16.(1)、计算:;(2)、解分式方程: .17. 如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.
 (1)、求证:AE=2CE;(2)、连接CD,请判断△BCD的形状,并说明理由.18. 如图,一次函数的图象与反比例函数的图象交于点 .
(1)、求证:AE=2CE;(2)、连接CD,请判断△BCD的形状,并说明理由.18. 如图,一次函数的图象与反比例函数的图象交于点 . (1)、求反比例函数与一次函数的表达式;(2)、若P为x轴上一点,的面积为5,求点P的坐标;(3)、结合图象,关于x的不等式的解集为 .19. 将正方形和菱形按照如图所示摆放,顶点D与顶点H重合,菱形的对角线经过点B,点E,G分别在 , 上.
(1)、求反比例函数与一次函数的表达式;(2)、若P为x轴上一点,的面积为5,求点P的坐标;(3)、结合图象,关于x的不等式的解集为 .19. 将正方形和菱形按照如图所示摆放,顶点D与顶点H重合,菱形的对角线经过点B,点E,G分别在 , 上.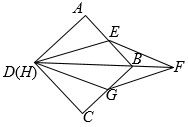 (1)、求证:;(2)、若 , 求的长.20. 我市于2021年5月22-23日在遂宁观音湖举行了“龙舟赛”,吸引了全国各地选手参加.现对某校初中1000名学生就“比赛规则”的了解程度进行了抽样调查(参与调查的同学只能选择其中一项),并将调查结果绘制出以下两幅不完整的统计图表,请根据统计图表回答下列问题:
(1)、求证:;(2)、若 , 求的长.20. 我市于2021年5月22-23日在遂宁观音湖举行了“龙舟赛”,吸引了全国各地选手参加.现对某校初中1000名学生就“比赛规则”的了解程度进行了抽样调查(参与调查的同学只能选择其中一项),并将调查结果绘制出以下两幅不完整的统计图表,请根据统计图表回答下列问题:类别
频数
频率
不了解
10
m
了解很少
16
0.32
基本了解
b
很了解
4
n
合计
a
1
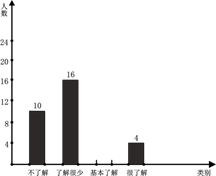 (1)、根据以上信息可知:a= , b= , m= , n=;(2)、补全条形统计图;(3)、估计该校1000名初中学生中“基本了解”的人数约有人;(4)、“很了解”的4名学生是三男一女,现从这4人中随机抽取两人去参加全市举办的“龙舟赛”知识竞赛,请用画树状图或列表的方法说明,抽到两名学生均为男生和抽到一男一女的概率是否相同.21. 2022北京冬奥会期间,某网店直接从工厂购进A、B两款冰墩墩钥匙扣,进货价和销售价如下表:(注:利润=销售价-进货价)
(1)、根据以上信息可知:a= , b= , m= , n=;(2)、补全条形统计图;(3)、估计该校1000名初中学生中“基本了解”的人数约有人;(4)、“很了解”的4名学生是三男一女,现从这4人中随机抽取两人去参加全市举办的“龙舟赛”知识竞赛,请用画树状图或列表的方法说明,抽到两名学生均为男生和抽到一男一女的概率是否相同.21. 2022北京冬奥会期间,某网店直接从工厂购进A、B两款冰墩墩钥匙扣,进货价和销售价如下表:(注:利润=销售价-进货价)类别价格
A款钥匙扣
B款钥匙扣
进货价(元/件)
30
25
销售价(元/件)
45
37
(1)、网店第一次用850元购进A、B两款钥匙扣共30件,求两款钥匙扣分别购进的件数;(2)、第一次购进的冰墩墩钥匙扣售完后,该网店计划再次购进A、B两款冰墩墩钥匙扣共80件(进货价和销售价都不变),且进货总价不高于2200元.应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少?(3)、冬奥会临近结束时,网店打算把B款钥匙扣调价销售.如果按照原价销售,平均每天可售4件.经调查发现,每降价1元,平均每天可多售2件,将销售价定为每件多少元时,才能使B款钥匙扣平均每天销售利润为90元?22. 如图,是的外接圆,点O在BC上,的角平分线交于点D,连接BD,CD,过点D作BC的平行线与AC的延长线相交于点P.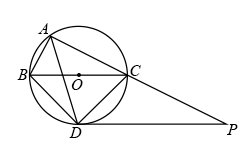 (1)、求证:PD是的切线;(2)、求证:∽;(3)、若 , , 求点O到AD的距离.23. 如图,抛物线与x轴交于点A和B,与y轴交于点C.
(1)、求证:PD是的切线;(2)、求证:∽;(3)、若 , , 求点O到AD的距离.23. 如图,抛物线与x轴交于点A和B,与y轴交于点C. (1)、求A、B、C三点坐标;(2)、如图1,动点P从点A出发,在线段上以每秒1个单位长度向点B做匀速运动,同时,动点Q从点B出发,在线段上以每秒个单位长度向点C做匀速运动,当其中一点到达终点时,另一点随之停止运动,连接 , 设运动时间为t秒,问P、Q两点运动多久后的面积S最大,最大面积是多少?(3)、如图2,点D为抛物线上一动点,直线交y轴于点E,直线交y轴于点F,求的值.
(1)、求A、B、C三点坐标;(2)、如图1,动点P从点A出发,在线段上以每秒1个单位长度向点B做匀速运动,同时,动点Q从点B出发,在线段上以每秒个单位长度向点C做匀速运动,当其中一点到达终点时,另一点随之停止运动,连接 , 设运动时间为t秒,问P、Q两点运动多久后的面积S最大,最大面积是多少?(3)、如图2,点D为抛物线上一动点,直线交y轴于点E,直线交y轴于点F,求的值.