山东省临沂市兰山区2023年中考一模数学试题
试卷更新日期:2023-05-05 类型:中考模拟
一、单选题
-
1. sin30°的值为( )A、 B、 C、 D、2. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )A、
 赵爽弦图
B、
赵爽弦图
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 科克曲线
D、
科克曲线
D、 斐波那契螺旋线
3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )
斐波那契螺旋线
3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,斑马线的作用是为了引导行人安全地通过马路.小丽觉得行人沿垂直马路的方向走过斑马线更为合理,这一想法体现的数学依据是( )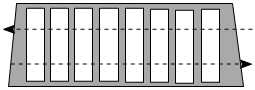 A、垂线段最短 B、两点确定一条直线 C、两点之间,线段最短 D、过直线外一点有且只有一条直线与已知直线平行5. 下列图形中,主视图和左视图一样的是( )A、
A、垂线段最短 B、两点确定一条直线 C、两点之间,线段最短 D、过直线外一点有且只有一条直线与已知直线平行5. 下列图形中,主视图和左视图一样的是( )A、 B、
B、 C、
C、 D、
D、 6. 一个正多边形的内角和是900度,则这个多边形是( )A、正六边形 B、正七边形 C、正八边形 D、正九边形7. 不等式组 的解集在数轴上可表示为( )A、
6. 一个正多边形的内角和是900度,则这个多边形是( )A、正六边形 B、正七边形 C、正八边形 D、正九边形7. 不等式组 的解集在数轴上可表示为( )A、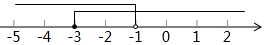 B、
B、 C、
C、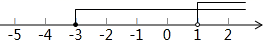 D、
D、 8. 某厂职工2020年的人均收入约为元,预计2022年的人均收入约为元,则人均收入的年平均增长率为( )A、1% B、1.21% C、10% D、12.1%9. 费尔兹奖是国际上享有崇高声誉的一个数学奖项,每四年评选一次,主要授予年轻的数学家.下面数据是部分获奖者获奖时的年龄(单位:岁):29,32,33,35,35,40,则这组数据的众数和中位数分别是( )A、35,35 B、34,33 C、34,35 D、35,3410. 如图,在中, , 以点B为圆心,适当长为半径画弧,交于点M,交于点N,分别以点M、N为圆心,大于的长为半径画弧,两弧在的内部相交于点P,画射线 , 交于点D,若 , 则的度数是( )
8. 某厂职工2020年的人均收入约为元,预计2022年的人均收入约为元,则人均收入的年平均增长率为( )A、1% B、1.21% C、10% D、12.1%9. 费尔兹奖是国际上享有崇高声誉的一个数学奖项,每四年评选一次,主要授予年轻的数学家.下面数据是部分获奖者获奖时的年龄(单位:岁):29,32,33,35,35,40,则这组数据的众数和中位数分别是( )A、35,35 B、34,33 C、34,35 D、35,3410. 如图,在中, , 以点B为圆心,适当长为半径画弧,交于点M,交于点N,分别以点M、N为圆心,大于的长为半径画弧,两弧在的内部相交于点P,画射线 , 交于点D,若 , 则的度数是( )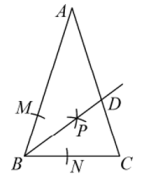 A、 B、 C、 D、11. 如图,以边长为2的等边△ABC顶点A为圆心、一定的长为半径画弧,恰好与BC边相切,分别交AB,AC于D,E,则图中阴影部分的面积是( )
A、 B、 C、 D、11. 如图,以边长为2的等边△ABC顶点A为圆心、一定的长为半径画弧,恰好与BC边相切,分别交AB,AC于D,E,则图中阴影部分的面积是( )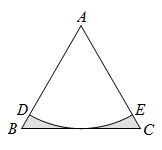 A、 B、 C、 D、12. 已知二次函数 , 当时,y的最小值为 , 则a的值为( )A、或4 B、或 C、或4 D、或4
A、 B、 C、 D、12. 已知二次函数 , 当时,y的最小值为 , 则a的值为( )A、或4 B、或 C、或4 D、或4二、填空题
-
13. 分解因式: .14. 一个不透明的箱子中有5个红球和若干个黄球,除颜色外无其它差别.若任意摸出一个球,摸出红球的概率为 , 则这个箱子中黄球的个数为个.15. 如图,在 中, ,过点B作 ,垂足为B , 且 ,连接CD , 与AB相交于点M , 过点M作 ,垂足为N . 若 ,则MN的长为 .
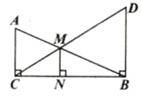 16. 如图,在正方形中,点E是边上的一点,点F在边的延长线上,且 , 连接交边于点G.过点A作 , 垂足为点M,交边于点N.若 , 则线段的长为 .
16. 如图,在正方形中,点E是边上的一点,点F在边的延长线上,且 , 连接交边于点G.过点A作 , 垂足为点M,交边于点N.若 , 则线段的长为 .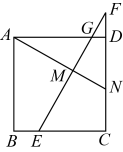
三、解答题
-
17.(1)、计算:(2)、解分式方程:18. 为减少传统塑料袋对生态环境的破坏,国家提倡使用可以在自然环境下(特定微生物、温度、湿度)较快完成降解的环保塑料袋.调查小组就某小区每户家庭1周内环保塑料袋的使用情况进行了抽样调查,使用情况为(不使用)、(1~3个)、(4~6个)、(7个及以上),以下是根据调查结果绘制的统计图的一部分.

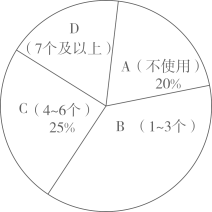 (1)、本次调查的样本容量是 ▲ , 请补全条形统计图;(2)、已知该小区有1500户家庭,调查小组估计:该小区1周内使用7个及以上环保塑料袋的家庭约有225户.调查小组的估计是否合理?请说明理由.19. 某数学小组要测量学校路灯的顶部到地面的距离,他们借助皮尺、测角仅进行测量,测量结果如下:
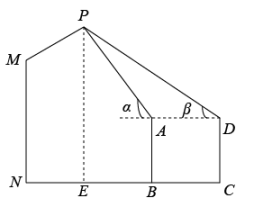
(1)、本次调查的样本容量是 ▲ , 请补全条形统计图;(2)、已知该小区有1500户家庭,调查小组估计:该小区1周内使用7个及以上环保塑料袋的家庭约有225户.调查小组的估计是否合理?请说明理由.19. 某数学小组要测量学校路灯的顶部到地面的距离,他们借助皮尺、测角仅进行测量,测量结果如下:测量项目
测量数据
从A处测得路灯顶部P的仰角
从D处测得路灯顶部P的仰角
测角仪到地面的距离
两次测量时测角仪之间的水平距离
计算路灯顶部到地面的距离约为多少米?(结果精确到0.1米.参考数据;)

 20. 如下图①和图②,并给出的关键信息有:哥哥、妹妹、家、书店.哥哥妹妹同时从家外出.
20. 如下图①和图②,并给出的关键信息有:哥哥、妹妹、家、书店.哥哥妹妹同时从家外出. (1)、请根据给出的关键信息以及两幅图,用精炼的语言创设一个问题情境,恰好能表达图①和图②中图像对应的函数关系.(2)、请根据(1)一种所创设的情境,用精炼的语言描述一下第30分钟时,两图中所表达的现实情境.(3)、请根据一中所创设的情境,第35分钟时图①和图②中速度更快的是填图①和图②.21. 如图,AB是⊙O的直径,点C,点D在⊙O上,AC=CD,AD与BC相交于点E,点F在BC的延长线上,且AF=AE.
(1)、请根据给出的关键信息以及两幅图,用精炼的语言创设一个问题情境,恰好能表达图①和图②中图像对应的函数关系.(2)、请根据(1)一种所创设的情境,用精炼的语言描述一下第30分钟时,两图中所表达的现实情境.(3)、请根据一中所创设的情境,第35分钟时图①和图②中速度更快的是填图①和图②.21. 如图,AB是⊙O的直径,点C,点D在⊙O上,AC=CD,AD与BC相交于点E,点F在BC的延长线上,且AF=AE.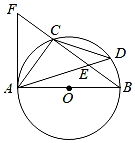 (1)、求证:AF是⊙O的切线;(2)、若EF=6,sin∠BAC= , 求⊙O的半径.22. 某山村经过脱贫攻坚和乡村振兴,经济收入持续增长.经统计,近五年该村甲农户年度纯收入如表所示:
(1)、求证:AF是⊙O的切线;(2)、若EF=6,sin∠BAC= , 求⊙O的半径.22. 某山村经过脱贫攻坚和乡村振兴,经济收入持续增长.经统计,近五年该村甲农户年度纯收入如表所示:年度(年)
2016
2017
2018
2019
2020
2021
年度纯收入(万元)
1.5
2.5
4.5
7.5
11.3
若记2016年度为第1年,在直角坐标系中用点(1,15),(2,2.5),(3,4.5),(4,7.5),(5,11.3)表示近五年甲农户纯收入的年度变化情况.如图所示 (m>0),y=x+b(k>0),y=ax2﹣0.5x+c(a>0),以便估算甲农户2021年度的纯收入.
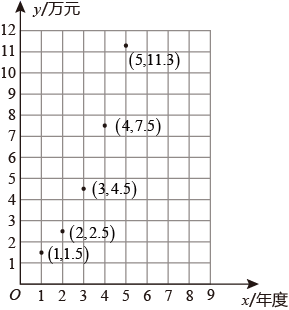 (1)、能否选用函数 (m>0)进行模拟,请说明理由;(2)、你认为选用哪个函数模拟最合理,请说明理由;(3)、甲农户准备在2021年底购买一台价值16万元的农机设备,根据(2)中你选择的函数表达式,预测甲农户2021年度的纯收入能否满足购买农机设备的资金需求.23. 问题解决:如图1,在矩形 中,点 分别在 边上, 于点 .
(1)、能否选用函数 (m>0)进行模拟,请说明理由;(2)、你认为选用哪个函数模拟最合理,请说明理由;(3)、甲农户准备在2021年底购买一台价值16万元的农机设备,根据(2)中你选择的函数表达式,预测甲农户2021年度的纯收入能否满足购买农机设备的资金需求.23. 问题解决:如图1,在矩形 中,点 分别在 边上, 于点 .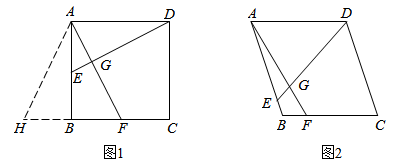 (1)、求证:四边形 是正方形;(2)、延长 到点 ,使得 ,判断 的形状,并说明理由.
(1)、求证:四边形 是正方形;(2)、延长 到点 ,使得 ,判断 的形状,并说明理由.类比迁移:如图2,在菱形 中,点 分别在 边上, 与 相交于点 , ,求 的长.