山东省德州市德城区2023年中考一模数学试题
试卷更新日期:2023-05-05 类型:中考模拟
一、单选题
-
1. ﹣3的相反数是( )A、 B、 C、-3 D、32. 下面四幅图是我国一些博物馆的标志,其中既是轴对称图形又是中心对称图形的是( )A、温州博物馆
 B、西藏博物馆
B、西藏博物馆 C、广东博物馆
C、广东博物馆 D、湖北博物馆
D、湖北博物馆 3. 一块直角三角板和一把直尺如图摆放,直尺的一边经过三角板的顶点 , 若 , 则的度数为( )
3. 一块直角三角板和一把直尺如图摆放,直尺的一边经过三角板的顶点 , 若 , 则的度数为( ) A、 B、 C、 D、4. 与最接近的整数是( )A、3 B、4 C、5 D、65. 某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )
A、 B、 C、 D、4. 与最接近的整数是( )A、3 B、4 C、5 D、65. 某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )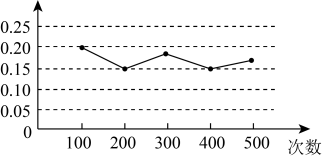 A、袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球 B、掷一枚质地均匀的硬币,落地时结果是“正面向上” C、掷一个质地均匀的正六面体骰子,落地时面朝上的点数是2 D、从一副扑克牌中随机抽取一张,抽到的牌是梅花6. 幻方历史悠久,传说最早出现在夏禹时代的“洛书”.洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图1),将9个数填在的方格中,如果满足每行、每列,每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图2的主格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则的值为( )
A、袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球 B、掷一枚质地均匀的硬币,落地时结果是“正面向上” C、掷一个质地均匀的正六面体骰子,落地时面朝上的点数是2 D、从一副扑克牌中随机抽取一张,抽到的牌是梅花6. 幻方历史悠久,传说最早出现在夏禹时代的“洛书”.洛书用今天的数学符号翻译出来,就是一个三阶幻方(如图1),将9个数填在的方格中,如果满足每行、每列,每条对角线上的三个数字之和都相等,就得到一个广义的三阶幻方.图2的主格中填写了一些数字和字母,若能构成一个广义的三阶幻方,则的值为( ) A、0 B、1 C、3 D、67. 某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m个人共同完成需n天,选取6组数对 ,在坐标系中进行描点,则正确的是()A、
A、0 B、1 C、3 D、67. 某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m个人共同完成需n天,选取6组数对 ,在坐标系中进行描点,则正确的是()A、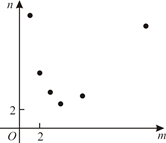 B、
B、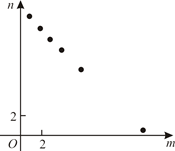 C、
C、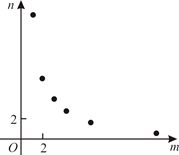 D、
D、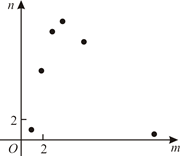 8. 关于 , 的方程组的解中与的和不小于5,则的取值范围为( )A、 B、 C、 D、9. 如图,在 中, .小丽按照下列方法作图:
8. 关于 , 的方程组的解中与的和不小于5,则的取值范围为( )A、 B、 C、 D、9. 如图,在 中, .小丽按照下列方法作图:①作 的角平分线 ,交 于点D;
②作 的垂直平分线,交 于点E .
根据小丽画出的图形,判断下列说法中正确的是( )
 A、点E是 的外心 B、点E是 的内心 C、点E在 的平分线上 D、点E到 边的距离相等10. 已知整数 , , , , 满足下列条件: , 以此类推,的值为( )A、-2023 B、-2022 C、-1012 D、-101111. 如图,△AOC中三个顶点的坐标分别为(4,0)、(0,0)、(4,3),AP为△AOC中线,以O为位似中心,把△AOP每条边扩大到原来的2倍,得到 , 则的长为( )
A、点E是 的外心 B、点E是 的内心 C、点E在 的平分线上 D、点E到 边的距离相等10. 已知整数 , , , , 满足下列条件: , 以此类推,的值为( )A、-2023 B、-2022 C、-1012 D、-101111. 如图,△AOC中三个顶点的坐标分别为(4,0)、(0,0)、(4,3),AP为△AOC中线,以O为位似中心,把△AOP每条边扩大到原来的2倍,得到 , 则的长为( ) A、 B、 C、或 D、或12. 如图,已知△ABC内接于半径为1的⊙O,∠BAC=θ(θ是锐角),则△ABC的面积的最大值为( )
A、 B、 C、或 D、或12. 如图,已知△ABC内接于半径为1的⊙O,∠BAC=θ(θ是锐角),则△ABC的面积的最大值为( )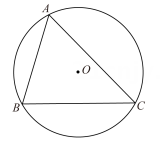 A、cosθ(1+cosθ) B、cosθ(1+sinθ) C、sinθ(1+sinθ) D、sinθ(1+cosθ)
A、cosθ(1+cosθ) B、cosθ(1+sinθ) C、sinθ(1+sinθ) D、sinθ(1+cosθ)二、填空题
-
13. 分解因式: .14. 若一元二次方程的两根互为相反数,则的值为 .15. 如图,四边形为平行四边形,则点的坐标为 .
 16. 在中, , , , 以一条直角边所在直线为轴,把旋转1周,得到圆锥,则该圆锥的侧面积最大值为 .17. 二次函数的部分对应值列表如下:
16. 在中, , , , 以一条直角边所在直线为轴,把旋转1周,得到圆锥,则该圆锥的侧面积最大值为 .17. 二次函数的部分对应值列表如下:x
…
-3
0
1
3
5
…
y
…
7
-8
-9
-5
7
…
则一元二次方程的解为 .
18. 我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是 .
三、解答题
-
19. 先化简,再求值: , 其中是不等式组的整数解.20. 为庆祝建党100周年,让同学们进一步了解中国科技的快速发展,长沙市某中学九(1)班团支部组织了一次手抄报比赛,该班每位旧学从A.“中国天眼”;B.“5G时代”;C.“夸父一号”;D.“巅峰使命”四主题中任选一个自己喜欢的主题.统计同学们所选主题的频数,绘制不完整的统计图,请根据统计图中的信息解答下列问题:
 (1)、九(1)班共有名学生;(2)、请以九(1)班的统计数据估计全校2000名学生大约有多少人选择D主题?(3)、D主题所对应扇形圆心角的大小为;(4)、甲和乙从A、B、C、D四个主题中任选一个主题,请用画树状图的方法求出他们选择相同主题的概率.21. 某综合实践小组开展了测量本校旗杆高度的实践活动.为了减小测量误差.小组在测量仰角的度数以及两个测点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,测量数据如下表(不完整).
(1)、九(1)班共有名学生;(2)、请以九(1)班的统计数据估计全校2000名学生大约有多少人选择D主题?(3)、D主题所对应扇形圆心角的大小为;(4)、甲和乙从A、B、C、D四个主题中任选一个主题,请用画树状图的方法求出他们选择相同主题的概率.21. 某综合实践小组开展了测量本校旗杆高度的实践活动.为了减小测量误差.小组在测量仰角的度数以及两个测点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,测量数据如下表(不完整).课题
测量旗杆的高度
成员
组长××× 组员:×××,×××,×××
测量工具
测量角度的仪器、皮尺等
测量示意图

说明:左图为测量示意图,线段表示学校旗杆,测量角度的仪器的高度 , 测点 , 与在同一条水平直线上, , 之间的距离可以直接测得,且点 , , , , , 都在同一竖直平面内.点 , , 在同一条直线上,点在上.
测量数据
测量项目
第一次
第二次
平均值
的度数
的度数
, 之间的距离
 (1)、任务一:两次测量, , 之间距离的平均值是;(2)、任务二:根据以上测量结果,请你帮助该综合实践小组求出学校旗杆的高度.
(1)、任务一:两次测量, , 之间距离的平均值是;(2)、任务二:根据以上测量结果,请你帮助该综合实践小组求出学校旗杆的高度.(参考数据: , , , , , )
22. 【调查活动】小峰同学为了完成老师布置的社会活动作业:《A市初中生阅读水平的现状》,随机走访了A市的甲、乙两所初中,收集到如下信息:
①甲、乙两校图书室各藏书18000册;
②甲校比乙校人均图书册数多2册;
③甲校的学生人数比乙校的人数少10%.
【问题解决】
请你根据上述三个信息,就甲、乙两校的“人数”或“人均图书册数”提出一个用分式方程解决的问题,并写出解题过程.
23. 如图,内接于半圆 , 是直径,过作直线 , 使 . (1)、求证:是半圆的切线;(2)、已知弧的中点 , 要求过作于 . (尺规作图,保留作图痕迹)(3)、若 , , 求 .24.(1)、【实验】如图①,点为线段的中点,线段与相交于点 , 当时,四边形的形状为;
(1)、求证:是半圆的切线;(2)、已知弧的中点 , 要求过作于 . (尺规作图,保留作图痕迹)(3)、若 , , 求 .24.(1)、【实验】如图①,点为线段的中点,线段与相交于点 , 当时,四边形的形状为;
A.矩形 B.菱形 C.正方形 D.平行四边形
其理论依据是 .
(2)、【探究】如图②,在平行四边形中,点是中点,过点作的垂线交边于点 , 连接 , 试猜想 , , 三条线段之间的数量关系,并给予证明. (3)、【应用】如图③,在中,点为的中点,若 , , , 求的面积.
(3)、【应用】如图③,在中,点为的中点,若 , , , 求的面积. 25. 如图,抛物线与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.
25. 如图,抛物线与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.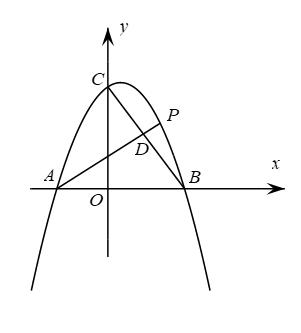 (1)、A,B,C三点的坐标为 , , ;(2)、连接 , 交线段于点D,
(1)、A,B,C三点的坐标为 , , ;(2)、连接 , 交线段于点D,①当与x轴平行时,求的值;
②当与x轴不平行时,求的最大值;
(3)、连接 , 是否存在点P,使得 , 若存在,求m的值,若不存在,请说明理由.