辽宁省抚顺市东洲区2023年中考二模数学试卷
试卷更新日期:2023-05-05 类型:中考模拟
一、单选题
-
1. 下列函数中,y是x的反比例函数的是( )A、 B、 C、 D、2. 如图所示的几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列各组图形不是相似图形的是( )A、
3. 下列各组图形不是相似图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 若反比例函数在每个象限内,随的增大而减小,则的值可能是( )A、-1 B、0 C、 D、15. 如图,一辆自行车竖直摆放在水平地面上,右边是它的部分示意图,现测得 , , , 则点A到的距离为( )
4. 若反比例函数在每个象限内,随的增大而减小,则的值可能是( )A、-1 B、0 C、 D、15. 如图,一辆自行车竖直摆放在水平地面上,右边是它的部分示意图,现测得 , , , 则点A到的距离为( ) A、 B、 C、 D、6. 三根等高的木杆竖直立在平地上,其俯视图如图所示,在某一时刻三根木杆在太阳光下的影子合理的是( )
A、 B、 C、 D、6. 三根等高的木杆竖直立在平地上,其俯视图如图所示,在某一时刻三根木杆在太阳光下的影子合理的是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 如图,在一间屋子里的屋顶上挂着一盏白炽灯,在它的正下方有一个球,下列说法:①球在地面上的影子是圆;②当球向上移动时,它的影子会增大;③当球向下移动时,它的影子会增大;④当球向上或向下移动时,它的影子大小不变,其中正确的有( )
7. 如图,在一间屋子里的屋顶上挂着一盏白炽灯,在它的正下方有一个球,下列说法:①球在地面上的影子是圆;②当球向上移动时,它的影子会增大;③当球向下移动时,它的影子会增大;④当球向上或向下移动时,它的影子大小不变,其中正确的有( ) A、0个 B、1个 C、2个 D、3个8. 如图,已知∠1=∠2,那么添加一个条件后,仍不能判定△ABC 与△ADE 相似 的是( )
A、0个 B、1个 C、2个 D、3个8. 如图,已知∠1=∠2,那么添加一个条件后,仍不能判定△ABC 与△ADE 相似 的是( )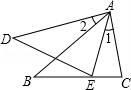 A、∠C=∠AED B、∠B=∠D C、 = D、 =9. 如图,在正方形网格中,的顶点均在格点上,则的值为( )
A、∠C=∠AED B、∠B=∠D C、 = D、 =9. 如图,在正方形网格中,的顶点均在格点上,则的值为( ) A、 B、 C、 D、10. 如图,中, , , , D是边上一动点(不与A,C两点重合),沿的路径移动,过点D作 , 交于点E,将沿直线折叠得到 . 若设 , 与重叠部分的面积为y,则下列图象能大致反映y与x之间函数关系的是( )
A、 B、 C、 D、10. 如图,中, , , , D是边上一动点(不与A,C两点重合),沿的路径移动,过点D作 , 交于点E,将沿直线折叠得到 . 若设 , 与重叠部分的面积为y,则下列图象能大致反映y与x之间函数关系的是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 中, , , , 则的长是.12. 点 和点 均在反比例函数 (k为常数, )的图象上,则 .13. 已知中, , 都是锐角,且 , 则∠C=度.14. 如图, , 直线 , 与这三条平行线分别交于点 , , , 和点 , , . 已知 , , , 则的长为 .
 15. 如图, , 反比例函数的图象过点B,若点A的坐标为 , , 则.
15. 如图, , 反比例函数的图象过点B,若点A的坐标为 , , 则.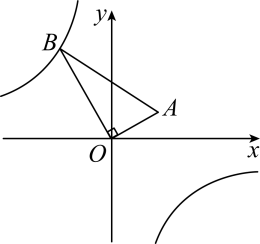 16. 如图,已知点 , 以点为位似中心,按的比例把缩小,则点的对应点的坐标为
16. 如图,已知点 , 以点为位似中心,按的比例把缩小,则点的对应点的坐标为 17. 在阳光下,一名同学测得一根长为1米的竹竿的影长为0.8米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,其影长为0.6米,落在地面上的影长为3.6米,则树高为米.
17. 在阳光下,一名同学测得一根长为1米的竹竿的影长为0.8米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,其影长为0.6米,落在地面上的影长为3.6米,则树高为米. 18. 如图,在平行四边形中, , E,F分别是上的动点,且 , 连接 , 与相交于P,过点P作 , 交于M,交于N,当E,F在上移动时,下列结论:①;②;③;④ . 其中正确的有 . (填序号)
18. 如图,在平行四边形中, , E,F分别是上的动点,且 , 连接 , 与相交于P,过点P作 , 交于M,交于N,当E,F在上移动时,下列结论:①;②;③;④ . 其中正确的有 . (填序号)
三、解答题
-
19.(1)、计算: .(2)、如图是一个几何体的三视图(单位:cm).

①这个几何体的名称是 ▲ ;
②根据图上的数据计算这个几何体的表面积(结果保留).
20. 在平面直角坐标系中,的三个顶点坐标分别为 , , .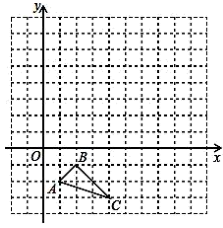
⑴画出关于轴对称的;
⑵以点为位似中心,在网格中画出的位似图形 , 使与的相似比为;
⑶设点为内一点,则依上述两次变换后点在内的对应点的坐标是 ▲ .
21. 如图,一次函数的图象与轴、轴分别相交于、两点,与反比例函数的图象相交于点 . (1)、求反比例函数的表达式;(2)、点的横坐标为4,过点作轴平行线,交反比例函数的图象于点 , 连接 求的面积.22. 小王和小李负责某企业宣传片的制作,期间要使用无人机采集一组航拍的资料.在航拍时,小王在处测得无人机的仰角为 , 同时小李登上斜坡的处测得无人机的仰角为 . 若小李所在斜坡的坡比为: , 铅垂高度米(点 , , , 在同一水平线上).
(1)、求反比例函数的表达式;(2)、点的横坐标为4,过点作轴平行线,交反比例函数的图象于点 , 连接 求的面积.22. 小王和小李负责某企业宣传片的制作,期间要使用无人机采集一组航拍的资料.在航拍时,小王在处测得无人机的仰角为 , 同时小李登上斜坡的处测得无人机的仰角为 . 若小李所在斜坡的坡比为: , 铅垂高度米(点 , , , 在同一水平线上). (1)、小王和小李两人之间的距离;(2)、此时无人机的高度 . ( , , , 结果精确到1米)23. 如图,是的外接圆,是的直径,是延长线上一点,连接 , 且 .
(1)、小王和小李两人之间的距离;(2)、此时无人机的高度 . ( , , , 结果精确到1米)23. 如图,是的外接圆,是的直径,是延长线上一点,连接 , 且 . (1)、求证:是的切线;(2)、若 , 求的值.24. 网络直播销售已经成为一种热门的销售方式,某生产商在一销售平台上进行直播销售板栗.已知板栗的成本价为6元/ , 每日销售量y()与销售单价x(元/)满足一次函数关系,下表记录的是有关数据,经销售发现,销售单价不低于成本价且不高于32元/ . 设公司销售板栗的日获利为w(元).
(1)、求证:是的切线;(2)、若 , 求的值.24. 网络直播销售已经成为一种热门的销售方式,某生产商在一销售平台上进行直播销售板栗.已知板栗的成本价为6元/ , 每日销售量y()与销售单价x(元/)满足一次函数关系,下表记录的是有关数据,经销售发现,销售单价不低于成本价且不高于32元/ . 设公司销售板栗的日获利为w(元).x(元/)
10
11
12
y()
4000
3900
3800
(1)、求出日销售量y与销售单价x之间的函数关系式并写出自变量的取值范围;(2)、当销售单价定为多少时,销售这种板栗日获利w最大?最大利润为多少元?25. 已知点O是四边形ABCD内一点,AB=BC,OD=OC,∠ABC=∠DOC=α. (1)、如图1,α=60°,探究线段AD与OB的数量关系,并加以证明;(2)、如图2,α=120°,探究线段AD与OB的数量关系,并说明理由;(3)、结合上面的活动经验探究,请直接写出如图3中线段AD与OB的数量关系为(直接写出答案)26. 如图,抛物线经过A(4,0),B(1,0)两点.
(1)、如图1,α=60°,探究线段AD与OB的数量关系,并加以证明;(2)、如图2,α=120°,探究线段AD与OB的数量关系,并说明理由;(3)、结合上面的活动经验探究,请直接写出如图3中线段AD与OB的数量关系为(直接写出答案)26. 如图,抛物线经过A(4,0),B(1,0)两点. (1)、求出抛物线的解析式;(2)、P是抛物线在第一象限上的一动点,过P作轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;(3)、若抛物线上有一点Q(点Q不与点B重合),使得点Q与点B到直线的距离相等,请直接写出点Q坐标.
(1)、求出抛物线的解析式;(2)、P是抛物线在第一象限上的一动点,过P作轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;(3)、若抛物线上有一点Q(点Q不与点B重合),使得点Q与点B到直线的距离相等,请直接写出点Q坐标.