辽宁省大连市高新园区2023年中考一模数学试题
试卷更新日期:2023-05-05 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、3 B、-3 C、 D、2. 如图,是由四个大小相同的小正方体拼成的几何体,则这个几何体的俯视图是( )
 A、
A、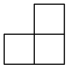 B、
B、 C、
C、 D、
D、 3. 北京时间2022年11月21日0点,万众瞩目的卡塔尔世界杯全面打响,据统计在小组赛的赛程中,场均观看直播人数达到了7062万人,则7062万用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,将三角板的直角顶点放在两条平行线、上,已知 , 则的度数为( )
3. 北京时间2022年11月21日0点,万众瞩目的卡塔尔世界杯全面打响,据统计在小组赛的赛程中,场均观看直播人数达到了7062万人,则7062万用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,将三角板的直角顶点放在两条平行线、上,已知 , 则的度数为( )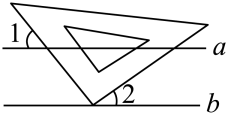 A、 B、 C、 D、6. 不等式组 的解集在数轴上表示正确的是( )A、
A、 B、 C、 D、6. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 7. 在我市开展的“好书伴我成长”读书活动中,某中学为了解八年级300名学生读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示:
7. 在我市开展的“好书伴我成长”读书活动中,某中学为了解八年级300名学生读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示:册数
0
1
2
3
4
人数
3
13
16
17
1
那么这50名同学读书册数的众数,中位数分别是( )
A、3,2 B、3,3 C、2,3 D、3,18. 若关于x的一元二次方程没有实数根,则实数m的取值范围是( )A、 B、 C、 D、9. 如图,在平行四边形中,以点B为圆心,适当长度为半径作弧,分别交 , 于点F,G,再分别以点F,G为圆心,大于长为半径作弧,两弧交于点H,作射线交于点E,连接 , 若 , , , 则的长为( )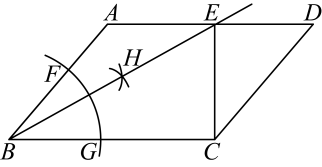 A、 B、 C、 D、10. 小明和小强两个人开车从甲地出发匀速行驶至乙地,小明先出发.在整个行驶过程中,小明和小强两人的车离开甲地的距离y(千米)与行驶的时间t(小时)之间的函数关系如图所示,有下列结论:①甲、乙两地相距300千米;②小强的车比小明的车晚出发1小时,却早到1个小时;③小强的车出发后1.5小时追上小明的车.其中正确的结论有( )
A、 B、 C、 D、10. 小明和小强两个人开车从甲地出发匀速行驶至乙地,小明先出发.在整个行驶过程中,小明和小强两人的车离开甲地的距离y(千米)与行驶的时间t(小时)之间的函数关系如图所示,有下列结论:①甲、乙两地相距300千米;②小强的车比小明的车晚出发1小时,却早到1个小时;③小强的车出发后1.5小时追上小明的车.其中正确的结论有( ) A、①② B、①③ C、②③ D、①②③
A、①② B、①③ C、②③ D、①②③二、填空题
-
11. 计算: .12. 在一个不透明的袋子里,装有2个红球和5个白球,这些球除颜色外没有任何区别,现从这个袋子中随机摸出一个球,“摸出红球”的概率是 .13. 点先向右平移2个单位,再向下平移1个单位后的坐标为 .14. 《九章算术》卷八方程【七】中记载:“今有牛五、羊二,值金十两.牛二、羊五,值金八两.牛、羊各值金几何?”题目大意是:5头牛、2只羊共值金10两,2头牛、5只羊共值金8两,每头牛、每只羊各值金多少两?若设一头牛值金x两,一只羊值金y两,则可列方程组为 .15. 如图,在中, , , , 以点A为圆心,为半径画弧,交于点D,则阴影部分的面积是 . (结果保留根号和)
 16. 如图,矩形纸片 , , 将矩形纸片折叠,使落在上,为折痕,然后将矩形纸片展开铺在一个平面上,将边折起,使点落在上的点处,连接 , 若 , 则(用含的代数式表示).
16. 如图,矩形纸片 , , 将矩形纸片折叠,使落在上,为折痕,然后将矩形纸片展开铺在一个平面上,将边折起,使点落在上的点处,连接 , 若 , 则(用含的代数式表示).
三、解答题
-
17. 计算: .18. 为了宣传垃圾分类,普及垃圾分类知识,让学生知道更多的垃圾分类知识,学校举行了垃圾分类相关知识竞赛.为了解这次竞赛成绩情况,抽取部分学生成绩作为样本,并将结果分为A、B、C、D四类,其中60分及以下为D类,分为C类,分为B类,100分为A类,绘制了如下的条形统计图和扇形统计图,请结合此图回答下列问题.
 (1)、此次抽样调查的样本容量为 , 竞赛成绩为B类的有人,扇形统计图中竞赛成绩为C类所对应的圆心角为°;(2)、若这次竞赛成绩为A类或B类的学生可获奖,全校共1200名学生,请估计全校获奖学生人数.19. 如图,点A、、、在同一条直线上,若 , , 求证: .
(1)、此次抽样调查的样本容量为 , 竞赛成绩为B类的有人,扇形统计图中竞赛成绩为C类所对应的圆心角为°;(2)、若这次竞赛成绩为A类或B类的学生可获奖,全校共1200名学生,请估计全校获奖学生人数.19. 如图,点A、、、在同一条直线上,若 , , 求证: .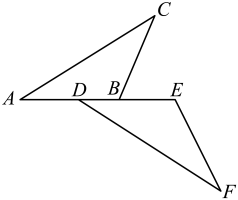 20. 如图,物业公司计划整理出一块矩形绿地,为充分利用现有资源,该矩形绿地一面靠墙(墙的长度为),另外三面用栅栏围成,已知栅栏总长度为 , 若矩形绿地的面积为 , 求矩形垂直于墙的一边,即的长.
20. 如图,物业公司计划整理出一块矩形绿地,为充分利用现有资源,该矩形绿地一面靠墙(墙的长度为),另外三面用栅栏围成,已知栅栏总长度为 , 若矩形绿地的面积为 , 求矩形垂直于墙的一边,即的长. 21. 我们知道当电压一定时,电流与电阻成反比例函数关系.现有某学生利用一个最大电阻为200欧姆的滑动变阻器及一电流表测电源电压,结果如图所示,当电阻R为6欧姆时,电流I为24安培.
21. 我们知道当电压一定时,电流与电阻成反比例函数关系.现有某学生利用一个最大电阻为200欧姆的滑动变阻器及一电流表测电源电压,结果如图所示,当电阻R为6欧姆时,电流I为24安培. (1)、求电流I(安培)关于电阻R(欧姆)的函数解析式;(2)、若 , 求电流I的变化范围.22. 如图,一艘渔船在黄海海域由西向东航行到达A处时,测得小岛C位于渔船的北偏东方向,该渔船再向东匀速航行2小时后到达B处,此时测得小岛C位于距离渔船30海里的北偏东方向.
(1)、求电流I(安培)关于电阻R(欧姆)的函数解析式;(2)、若 , 求电流I的变化范围.22. 如图,一艘渔船在黄海海域由西向东航行到达A处时,测得小岛C位于渔船的北偏东方向,该渔船再向东匀速航行2小时后到达B处,此时测得小岛C位于距离渔船30海里的北偏东方向. (1)、填空:;(2)、求渔船的速度(结果取整数).(参考数据: , , , )23. 是的直径,点C在上,于E交于点F,连接 , 点D在延长线上, .
(1)、填空:;(2)、求渔船的速度(结果取整数).(参考数据: , , , )23. 是的直径,点C在上,于E交于点F,连接 , 点D在延长线上, . (1)、如图1,求证:是的切线;(2)、如图2,过B作于M, , , 求的长.24. 如图,在中, , , , 动点D从点A出发,沿线段以的速度向终点B运动,当点D不与点A、B重合时,过D作于E,以、为邻边作 . 设点D的运动时间为 , 与重叠部分的面积为 .
(1)、如图1,求证:是的切线;(2)、如图2,过B作于M, , , 求的长.24. 如图,在中, , , , 动点D从点A出发,沿线段以的速度向终点B运动,当点D不与点A、B重合时,过D作于E,以、为邻边作 . 设点D的运动时间为 , 与重叠部分的面积为 .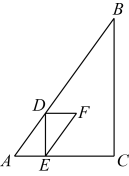 (1)、当点F在上时,求t的值;(2)、求S关于t的函数解析式,并直接写出自变量t的取值范围.25. 综合与实践
(1)、当点F在上时,求t的值;(2)、求S关于t的函数解析式,并直接写出自变量t的取值范围.25. 综合与实践问题情境:数学活动课上,王老师出示了一个问题:如图1,在中, , D是延长线上一点,连接 , , 点E在线段上,且 , 连接 .

求证 .
(1)、独立思考:请解答王老师提出的问题.(2)、实践探究:在原有问题条件不变的情况下,王老师增加下面的条件,并提出新问题,请你解答.“如图2,连接 , 以B为圆心,长为半径画弧,交于点F,连接 , 探究线段与之间的数量关系,并证明.”
(3)、问题解决:数学活动小组对上述问题进行特殊化研究之后,提出下面的问题,请你解答.“如图3,在(2)条件下,过E作于K,若 , , 求的长.”
26. 在平面直角坐标系中,抛物线与x轴交于点A,点 , 与y轴交于点C,点在抛物线上,点P是抛物线上的动点. (1)、求抛物线的解析式;(2)、如图1,连接 , 若平分 , 求点P的坐标;(3)、如图2,连接 , 抛物线的对称轴交于点E,连接 , 点P在y轴右侧的抛物线上,若 , 求点P的坐标.
(1)、求抛物线的解析式;(2)、如图1,连接 , 若平分 , 求点P的坐标;(3)、如图2,连接 , 抛物线的对称轴交于点E,连接 , 点P在y轴右侧的抛物线上,若 , 求点P的坐标.