吉林省长春市净月高新区2023年中考一模数学试题

试卷更新日期：2023-05-05 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算 $(- 2) \times 3$ 的结果等于（）

A、1 B、-1 C、6 D、-6

查看试题解析
2. 同学们，你们知道吗？2022年卡塔尔世界杯主场馆卢塞尔体育场，是中国铁建国际集团承建的，这是中国以设计施工总承包身份建设的首个世界杯体育场项目，广受好评，总耗资约767000000美元，这个数用科学记数法表示为（）

A、 $767 \times 1 0^{6}$ B、 $7.67 \times 1 0^{7}$ C、 $7.67 \times 1 0^{8}$ D、 $7.67 \times 1 0^{9}$

查看试题解析
3. 如图是由5个相同的正方体搭成的几何体，这个几何体的俯视图是（）

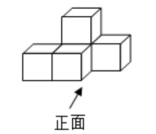A、 B、 C、 D、

查看试题解析
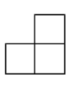4. 不等式组 ${\begin{array}{l} x - 1 \leq 1 \\ 2 x + 3 > 1 \end{array}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
5. 如图是某商场自动扶梯的示意图，自动扶梯 $A B$ 的坡角（ $∠ B A C$ ）为 $30.5 °$ ，乘客从扶梯底端升到顶端上升的高度 $B C$ 为5米，则自动扶梯 $A B$ 的长为（）

A、 $5 t a n 30.5 °$ 米 B、 $5 s i n 30.5 °$ 米 C、 $\frac{5}{s i n 30.5 °}$ 米 D、 $\frac{5}{c o s 30.5 °}$ 米

查看试题解析
6. 如图，四边形ADBC内接于⊙O，∠AOB＝122°，则∠ACB等于（　　）

A、131° B、119° C、122° D、58°

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ C = 84 °$ ，图中所作直线 $M N$ 与射线 $B D$ 交于点D，点D在 $A C$ 边上，根据图中尺规作图痕迹，判断以下结论正确的是（）

A、 $B C = B G$ B、 $∠ A B D = 30 °$ C、 $C D = G D$ D、 $∠ A B D = 32 °$

查看试题解析
8. 如图1是一个亮度可调节的台灯，其灯光亮度的改变，可以通过调节总电阻控制电流的变化来实现．如图2是该台灯的电流 $I (A)$ 与电阻 $R (Ω)$ 成反比例函数的图象，该图象经过点 $P (880 ， 0.25)$ ．根据图象可知，下列说法错误的是（）

A、 $I$ 与 $R$ 的函数关系式是 $I = \frac{220}{R} (R > 0)$ B、当 $I = 0.5$ 时， $R = 440$ C、当 $R > 1000$ 时， $I > 0.22$ D、当 $880 < R < 1000$ 时， $I$ 的取值范围是 $0.22 < I < 0.25$

查看试题解析

二、填空题

9. 分解因式： $a^{3} - 4 a$ ＝.

查看试题解析
10. 关于x的一元二次方程x²+2x﹣k=0有两个不相等的实数根，则k的取值范围是．

查看试题解析
11. 我国古代《孙子算经》中有记载“多人共车”问题：“今有三人共车，二车空；二人共车，九人步，问人与车各几何？”意思是“每3人共乘一辆车，最终剩余2辆车；每2人共乘一辆车，最终有9人无车可乘，问人和车的数量各是多少？”则乘车人数为人．

查看试题解析
12. 如图，矩形ABCD的对角线AC、BD相交于点O，分别以点A、C为圆心，AO长为半径画弧，分别交AB、CD于点E、F．若AC＝6，∠CAB＝30°，则图中阴影部分的面积为（结果保留π）

查看试题解析
13. 如图所示的网格是正方形网格，点A、B、C、D、E是网格线交点，则 $∠ D A E - ∠ B A C$ 的度数为度．

查看试题解析
14. 在平面直角坐标系 $x O y$ 中，若点 $A (m - 1 ， y_{1})$ ， $B (m ， y_{2})$ 在二次函数 $y = a x^{2} - 2 a x + 4$ $(a > 0)$ 的图像上，且总满足 $y_{1} > y_{2}$ ，则m的取值范围是．

查看试题解析

三、解答题

15. 先化简：再求值： $(2 x + 1) (2 x - 1) - {(2 x - 3)}^{2}$ ，其中 $x = 2$ ．

查看试题解析
16. 2022年11月29日，神舟十五号成功发射，作为中国空间站建造阶段最后一次飞行任务，标志着我国载人航天踏上新征程，某学校举办航天知识讲座，需要两名引导员，决定从A、B、C、D四名志愿者中，通过抽签的方式确定两人．抽签规则：将四名志愿者的名字分别写在四张完全相同且不透明卡片的正面，把四张卡片背面朝上，洗匀后放在桌面上，先从中随机抽取一张卡片，记下名字，再从剩余的三张卡片中随机抽取第二张，记下名字．

(1)、“A志愿者被选中”是事件（填“随机”或“不可能”或“必然”）；

(2)、用画树状图或列表的方法求出A、B两名志愿者同时被选中的概率．

查看试题解析
17. 2023年是中国农历癸卯兔年．春节前，某商场进货员预测一种“吉祥兔”布偶能畅销市场，就用4000元购进一批这种“吉祥兔”，面市后果然供不应求，商场又用8800元购进了第二批这种“吉祥兔”，所购数量是第一批购进量的2倍，但每件的进价贵了4元．该商场购进第一批、第二批“吉祥兔”每件的进价分别是多少元？

查看试题解析
18. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，点O在 $A B$ 上，以点O为圆心， $O A$ 长为半径的圆与 $A C$ 、 $A B$ 分别交于点D、E，且 $∠ C B D = ∠ A$ ．

(1)、求证： $B D$ 是 $⊙ O$ 的切线；

(2)、若 $A D ： A O = 5 ： 3$ ， $B C = 4$ ，则 $B D$ 的长为．

查看试题解析
19. 图①、图②、图③均是5×5的正方形网格，每个小正方形的边长均为1，其顶点称为格点， $△ A B C$ 的顶点均在格点上．只用无刻度的直尺，在给定的网格中，按下列要求作图，保留作图痕迹．

(1)、网格中 $△ A B C$ 的形状是．

(2)、在图①中确定一点D，连结 $D B 、 D C$ ，使 $△ D B C$ 与 $△ A B C$ 全等．

(3)、在图②中 $△ A B C$ 的边 $B C$ 上确定一点E，连结 $A E$ ，使 $△ A B E ∽ △ C B A$ ．

(4)、在图③中 $△ A B C$ 的边 $A B$ 上确定一点P，在边 $B C$ 上确定一点Q，连结 $P Q$ ，使 $△ P B Q ∽ △ A B C$ ，且相似比为 $3 ： 5$ ．

查看试题解析
20. 某校举办以2022年北京冬奥会为主题的知识竞赛，从七年级和八年级各随机抽取了50名学生的竞赛成绩进行整理、描述和分析，部分信息如下：
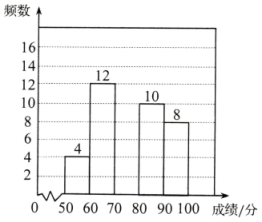
a：七年级抽取成绩的频数分布直方图如图．（数据分成5组， $50 \leq x < 60$ ， $60 \leq x < 70$ ， $70 \leq x < 80$ ， $80 \leq x < 90$ ， $90 \leq x \leq 100$ ）
b：七年级抽取成绩在7 $0 \leq x < 80$ 这一组的是：70，72，73，73，75，75，75，76，77，77，78，78，79，79，79，79．
c：七、八年级抽取成绩的平均数、中位数如下：
年级
平均数
中位数
七年级
76.5
m
八年级
78.2
79
请结合以上信息完成下列问题：

(1)、七年级抽取成绩在 $60 \leq x < 90$ 的人数是 ▲ ，并补全频数分布直方图；

(2)、表中m的值为；

(3)、七年级学生甲和八年级学生乙的竞赛成绩都是78，则（填“甲”或“乙”）的成绩在本年级抽取成绩中排名更靠前；

(4)、七年级的学生共有400人，请你估计七年级竞赛成绩90分及以上的学生人数．

查看试题解析
21. 甲乙两人相约一起去登山，登山过程中，甲先爬了100米、乙才开始追赶甲．甲、乙两人距地面的高度y（米）与登山时间x（分） $(x \geq 0)$ 之间的函数图象如图所示，根据图像所提供的信息解答下列问题：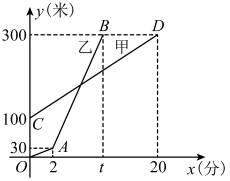

(1)、甲登山的速度是每分钟米；

(2)、若乙提速后，乙的速度是甲登山速度的3倍，请求出乙提速后距离地面的高度y（米）与登山时间x（分）之间的函数关系，并写出相应自变量取值范围；

(3)、直接写出甲乙相遇后，甲再经过多长时间与乙相距30米？

查看试题解析
22. 如图

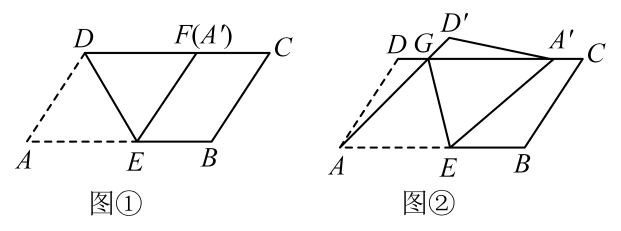(1)、【感知】如图①，将 $▱ A B C D$ 沿过点D的直线折叠，使点A落在 $C D$ 边上的点F处，得到折痕 $D E$ ，连结 $E F$ ．若 $A D = 4$ ，则四边形 $A E F D$ 的周长为．

(2)、【探究】如图②，将四边形 $A E G D$ 沿GE折叠，点A、D的对应点分别为 $A^{'}$ 、 $D^{'}$ ，点 $A^{'}$ 恰好落在 $C D$ 边上．
求证：四边形 $A E A^{'} G$ 为菱形．

(3)、若 $A B = 6$ ， $C B = 3$ ， $∠ B = 120 °$ ， $C A^{'} = 1$ ，则 $△ A^{'} G D^{'}$ 的面积为．

查看试题解析
23. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A B = 5$ ， $s i n A = \frac{3}{5}$ ．点P从点A出发，以每秒2个单位长度的速度向终点B匀速运动，过点P作 $P D ⊥ A B$ 交折线 $A C - C B$ 于点D，连结 $B D$ ，将 $△ D B P$ 绕点D逆时针旋转90°得到 $△ D E F$ ．设点P的运动时间为t（秒）．

(1)、 $A C =$ ．

(2)、用含t的代数式表示线段 $P D$ 的长．

(3)、当点E落在 $A B$ 边上时，求t的值．

(4)、当 $△ D E F$ 与 $△ A B C$ 重叠部分为三角形时，直接写出t的取值范围．

查看试题解析
24. 在平面直角坐标系中，抛物线 $y = - x^{2} + a x + 1$ （a为常数），经过点 $P (2 ， - 7)$ ，点Q在抛物线上，其横坐标为m，将此抛物线上P、Q两点间的部分（包括P、Q两点）记为图像G．

(1)、求抛物线的解析式．

(2)、若点B是抛物线上一点，横坐标为1．过点B作x轴的平行线交抛物线于另一点C，连结 $B C$ ，求 $△ P B C$ 的面积．

(3)、当抛物线的顶点是图像G的最高点，且图像G的最高点与最低点到x轴的距离和为定值时，求m的取值范围．

(4)、已知点 $M (2 m - 1 ， - 7)$ 、 $N (2 m - 1 ， \frac{1}{2} m + 1)$ 、 $E (2 ， \frac{1}{2} m + 1)$ ，顺次连接 $P M 、 M N 、 N E 、 E P$ 得到矩形 $P M N E$ ，当图像G与该矩形的边有两个公共点时，直接写出m的取值范围．

查看试题解析

年级	平均数	中位数
七年级	76.5	m
八年级	78.2	79