河北省唐山市2023年中考一模数学试题
试卷更新日期:2023-05-05 类型:中考模拟
一、单选题
-
1. 在实数 , , 0,-1中,最小的数是( )A、-1 B、0 C、 D、2. 如图,点C到直线的距离是( )
 A、线段的长度 B、线段的长度 C、线段的长度 D、线段的长度3. 如图,数轴上表示 的相反数的点是( )
A、线段的长度 B、线段的长度 C、线段的长度 D、线段的长度3. 如图,数轴上表示 的相反数的点是( )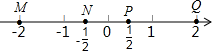 A、M B、N C、P D、Q4. 下列垃圾分类标识的图案既是轴对称图形,又是中心对称图形的是( )A、
A、M B、N C、P D、Q4. 下列垃圾分类标识的图案既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 大小在 和 之间的整数有( )A、0个 B、1个 C、2个 D、3个6. 某同学的作业如下框,其中※处填的依据是( )
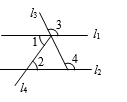
5. 大小在 和 之间的整数有( )A、0个 B、1个 C、2个 D、3个6. 某同学的作业如下框,其中※处填的依据是( )如图,已知直线 .若 ,则 .
请完成下面的说理过程.
解:已知 ,
根据(内错角相等,两直线平行),得 .
再根据( ※ ),得 .
 A、两直线平行,内错角相等 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,同旁内角互补7. 计算( )A、1 B、 C、 D、8. 如图所示的几何体由六块相同的小正方体搭成,若移走一块小正方体几何体的左视图发生了改变,则移走的小正方体是( )
A、两直线平行,内错角相等 B、内错角相等,两直线平行 C、两直线平行,同位角相等 D、两直线平行,同旁内角互补7. 计算( )A、1 B、 C、 D、8. 如图所示的几何体由六块相同的小正方体搭成,若移走一块小正方体几何体的左视图发生了改变,则移走的小正方体是( ) A、① B、② C、③ D、④9.
A、① B、② C、③ D、④9.某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
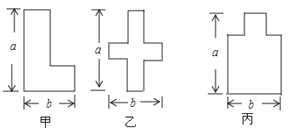 A、甲种方案所用铁丝最长 B、乙种方案所用铁丝最长 C、丙种方案所用铁丝最长 D、三种方案所用铁丝一样长10. 若 , 运算的结果为整式,则“□”中的式子可能是( )A、y-x B、y+x C、2x D、11. 若一组数据 , , 的平均数为4,方差为3,那么数据 , , 的平均数和方差分别是( )A、4, 3 B、6 3 C、3 4 D、6
A、甲种方案所用铁丝最长 B、乙种方案所用铁丝最长 C、丙种方案所用铁丝最长 D、三种方案所用铁丝一样长10. 若 , 运算的结果为整式,则“□”中的式子可能是( )A、y-x B、y+x C、2x D、11. 若一组数据 , , 的平均数为4,方差为3,那么数据 , , 的平均数和方差分别是( )A、4, 3 B、6 3 C、3 4 D、6 5
12. 有三种不同质量的物体“■”“▲”“●”,其中同一种物体的质量都相等.下列四个天平中只有一个天平没有处于平衡状态,则该天平是( )A、
5
12. 有三种不同质量的物体“■”“▲”“●”,其中同一种物体的质量都相等.下列四个天平中只有一个天平没有处于平衡状态,则该天平是( )A、 B、
B、 C、
C、 D、
D、 13. 如图,在中, , , 以A为圆心,任意长为半径画弧分别交、于点M和N,再分别以M、N为圆心,大于的长为半径画弧,两弧交于点P,连结并延长交于点D,则等于( )
13. 如图,在中, , , 以A为圆心,任意长为半径画弧分别交、于点M和N,再分别以M、N为圆心,大于的长为半径画弧,两弧交于点P,连结并延长交于点D,则等于( ) A、 B、 C、 D、14. 如图,正六边形的边长为1,连接 , 则图中阴影四边形的周长为( )
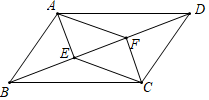
A、 B、 C、 D、14. 如图,正六边形的边长为1,连接 , 则图中阴影四边形的周长为( ) A、3 B、4 C、 D、15. 《九章算术》是中国古代数学著作之一,书中有这样一个问题:五只雀、六只燕共重一斤;雀重燕轻,互换其中一只,恰好一样重.问:每只雀、燕的重量各为多少?设一只雀的重量为x斤,一只燕的重量为y斤,则正确的是( )A、依题意 B、依题意 C、一只雀的重量为斤 D、一只燕的重量为斤16. 如图,▱ABCD中,要在对角线BD上找点E、F,使四边形AECF为平行四边形,现有甲、乙、丙三种方案,则正确的方案是( )
A、3 B、4 C、 D、15. 《九章算术》是中国古代数学著作之一,书中有这样一个问题:五只雀、六只燕共重一斤;雀重燕轻,互换其中一只,恰好一样重.问:每只雀、燕的重量各为多少?设一只雀的重量为x斤,一只燕的重量为y斤,则正确的是( )A、依题意 B、依题意 C、一只雀的重量为斤 D、一只燕的重量为斤16. 如图,▱ABCD中,要在对角线BD上找点E、F,使四边形AECF为平行四边形,现有甲、乙、丙三种方案,则正确的方案是( )甲:只需要满足BE=DF
乙:只需要满足AE=CF
丙:只需要满足AE∥CF
 A、甲、乙、丙都是 B、只有甲、丙才是 C、只有甲、乙才是 D、只有乙、丙才是
A、甲、乙、丙都是 B、只有甲、丙才是 C、只有甲、乙才是 D、只有乙、丙才是二、填空题
-
17. 一个不透明的袋子里装有3个红球和5个黑球,它们除颜色外其余都相同.从袋中任意摸出一个球是红球的概率为.18. 如图,在等边中,直尺的一边与重合,另一边分别交于点D,E.点B,C,D,E处读数分别为18,14,1,3,则
 (1)、等边的边长为cm;(2)、直尺的宽为cm.19. 如图,已知点 , (),点P为线段上的一个动点,反比例函数(k为常数,)的图象经过点P.
(1)、等边的边长为cm;(2)、直尺的宽为cm.19. 如图,已知点 , (),点P为线段上的一个动点,反比例函数(k为常数,)的图象经过点P. (1)、当点P与点M重合时,;(2)、若点P与点N重合时, , 此时点到直线的距离为 .
(1)、当点P与点M重合时,;(2)、若点P与点N重合时, , 此时点到直线的距离为 .三、解答题
-
20. 某市计划修建一个长为米,宽为米的矩形市民休闲广场.(1)、请计算该广场的面积S(结果用科学记数法表示);(2)、如果用一种正方形大理石地砖铺装该广场地面,请计算需要多少块大理石地砖.21. 如图,A,B两地相距1000m,嘉嘉从A地出发,沿方向以的速度行进,淇淇从B地出发,沿方向以的速度行进,两人同时出发,设行进的时间为 .
 (1)、用含t的代数式表示:
(1)、用含t的代数式表示:①两人行进的路程之和;
②当时,两人之间的距离;
(2)、当(s)时,真接写出两人之间的距离.22. 为了倡导环境保护,某校开展废旧电池回收活动.德育处从本校学生中随机调查了50名学生上交废旧电池的数量情况,并制作了统计图(如图): (1)、求这50名学生上交废旧电池在节(8节电池数量节)的学生人数;(2)、如果把图中每组废旧电池数量值用该组的中间值(如的中间值为2,的中间值为6)来代替,估计该校平均每名学生上交废旧电池的数量;(3)、从这50名学生上交废旧电池数量在节的学生中,任意抽取2名学生,直接写出至少有1名学生上交废旧电池数量在节的概率.23. 已知如图,是腰长为4的等腰直角三角形, , 以A为圆心,2为半径作半圆A,交所在直线于点M,N.点E是半圆A上仟意一点.连接 , 把绕点B顺时针旋转90°到的位置,连接 , .
(1)、求这50名学生上交废旧电池在节(8节电池数量节)的学生人数;(2)、如果把图中每组废旧电池数量值用该组的中间值(如的中间值为2,的中间值为6)来代替,估计该校平均每名学生上交废旧电池的数量;(3)、从这50名学生上交废旧电池数量在节的学生中,任意抽取2名学生,直接写出至少有1名学生上交废旧电池数量在节的概率.23. 已知如图,是腰长为4的等腰直角三角形, , 以A为圆心,2为半径作半圆A,交所在直线于点M,N.点E是半圆A上仟意一点.连接 , 把绕点B顺时针旋转90°到的位置,连接 , .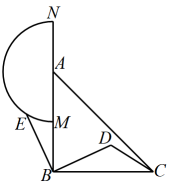 (1)、求证:;(2)、当与半圆A相切时,求弧的长;(3)、直接写出面积的最大值.24. 如图,直线分别与x轴、y轴交于A,B两点,直线与交于点 , 与x轴交于点 , 点M在线段上,直线轴于点E,与交于点N.
(1)、求证:;(2)、当与半圆A相切时,求弧的长;(3)、直接写出面积的最大值.24. 如图,直线分别与x轴、y轴交于A,B两点,直线与交于点 , 与x轴交于点 , 点M在线段上,直线轴于点E,与交于点N. (1)、求直线的表达式;(2)、设点M的横坐标为m.
(1)、求直线的表达式;(2)、设点M的横坐标为m.①当时,求线段的长;
②若点M,N,E三点中,其中两点恰好关于第三点对称,直接写出此时m的值.
25. 某水果店包装一种果篮需要A,B两种水果,A种水果的单价比B种水果单价少3元,若用600元购进A种水果和用900元购进B种水果数量一样多,包装一盒果篮需要A种水果4斤和B种水果2斤,每盒还需包装费8元.市场调查发现:设每盒果篮的售价是x元(x是整数),该果篮每月的销量Q(盒)与售价x(元)的关系式为 .(1)、求一盒果篮的成本(成本进价包装费);(2)、若每月的利润是w元,求w关于x的函数解析式(不需要写出自变量的取值范围);(3)、若每盒果篮的售价不超过a元(a是大于70的常数,且是整数),直接写出每月的最大利润.26. 如图1和图2,在四边形中, , , , , 点K在边上,点M,N分别在 , 边上,且 , 点P从点M出发沿折线匀速运动,点E在边所在直线上随P移动,且始终保持;点Q从点D出发沿匀速运动,点P,Q同时出发,点Q的速度是点P的一半,点P到达点N停止,点Q随之停止.设点P移动的路程为x.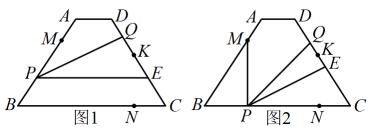 (1)、当时,求的长;(2)、当时,求x的值;(3)、用含x的式子表示的长;(4)、已知点P从点M到点B再到点N共用时20秒,若 , 请直接写出点K在线段上(包括端点)的总时长.
(1)、当时,求的长;(2)、当时,求x的值;(3)、用含x的式子表示的长;(4)、已知点P从点M到点B再到点N共用时20秒,若 , 请直接写出点K在线段上(包括端点)的总时长.