河北省唐山市丰南区2023年中考一模测数学试卷
试卷更新日期:2023-05-05 类型:中考模拟
一、单选题
-
1. 下列图形中,能确定的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,正八边形是轴对称图形,对称轴可以是直线( )
2. 如图,正八边形是轴对称图形,对称轴可以是直线( ) A、 B、 C、 D、3. 今年以来,河北持续推进学雷锋志愿服务活动,通过抓队伍,建平台、强阵地,更好地发挥党员干部模范带头作用,努力形成人人学雷锋、人人做雷锋、人人敬雷锋的生动局面.目前,全省共有1155万多名志愿者、5万多个志愿服务组织.其中数据1155万可以表示为( )A、 B、 C、 D、4. 如图,从地观测地,发现地在地的北偏东方向上,则从地观测地,可知地在地的( )
A、 B、 C、 D、3. 今年以来,河北持续推进学雷锋志愿服务活动,通过抓队伍,建平台、强阵地,更好地发挥党员干部模范带头作用,努力形成人人学雷锋、人人做雷锋、人人敬雷锋的生动局面.目前,全省共有1155万多名志愿者、5万多个志愿服务组织.其中数据1155万可以表示为( )A、 B、 C、 D、4. 如图,从地观测地,发现地在地的北偏东方向上,则从地观测地,可知地在地的( ) A、北偏东方向上 B、南偏西方向上 C、北偏东方向上 D、南偏西方向上5. 如图所示的几何体是由9个大小相同的小正方体组成的,将小正方体①移走后,所得几何体的三视图没有发生变化的是( )
A、北偏东方向上 B、南偏西方向上 C、北偏东方向上 D、南偏西方向上5. 如图所示的几何体是由9个大小相同的小正方体组成的,将小正方体①移走后,所得几何体的三视图没有发生变化的是( )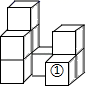 A、主视图和左视图 B、主视图和俯视图 C、左视图和俯视图 D、主视图、左视图、俯视图6. 如图,将△AOB绕点O按逆时针方向旋转60°后得到△COD,若∠AOB=15°,则∠AOD的度数是( )
A、主视图和左视图 B、主视图和俯视图 C、左视图和俯视图 D、主视图、左视图、俯视图6. 如图,将△AOB绕点O按逆时针方向旋转60°后得到△COD,若∠AOB=15°,则∠AOD的度数是( )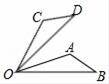 A、15° B、45° C、60° D、75°7. 计算 的正确结果是( )
A、15° B、45° C、60° D、75°7. 计算 的正确结果是( )
A、 B、 C、 D、8. 下列选项中的尺规作图,能推出PA=PC的是( )A、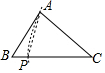 B、
B、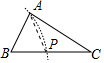 C、
C、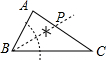 D、
D、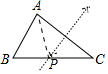 9. 若(x+3)(x+n)=x2+mx-15,则m的值为( )A、-2 B、2 C、5 D、-510. 图1是小明爸爸给小明出的一道题,图2是小明对该题的解答.他所写结论正确的个数是( )
9. 若(x+3)(x+n)=x2+mx-15,则m的值为( )A、-2 B、2 C、5 D、-510. 图1是小明爸爸给小明出的一道题,图2是小明对该题的解答.他所写结论正确的个数是( )表示实数 , , , 的点在数轴上的位置如图所示,

请写出六个不同的结论.
①四个数中,最小的是;②;
③;
④;
⑤;
⑥ .
图1
图2
A、3 B、4 C、5 D、611. 一次数学测试,某小组5名同学的成绩统计如下(有两个数据被遮盖):组员
甲
乙
丙
丁
戊
平均成绩
众数
得分
则被遮盖的两个数据依次是( )
A、 B、 C、 D、12. 如图,在平面直角坐标系中,的顶点为 , , . 以点为位似中心,在第三象限内作与的位似比为的位似图形 , 则点的坐标为( ) A、 B、 C、 D、13. 某校七年级(2)班40名同学,为探望福利院的小朋友捐款买礼物,共捐了100元,捐款情况如下表:
A、 B、 C、 D、13. 某校七年级(2)班40名同学,为探望福利院的小朋友捐款买礼物,共捐了100元,捐款情况如下表:捐款/元
1
2
3
4
人数
6
※
※
7
表格中捐款2元和3元的人数不小心被墨水污染已经看不清楚,设捐款2元的有名同学,捐款3元的有名同学.根据题意,所列方程组正确的为( )
A、 B、 C、 D、14. 老师在微信群发了这样一个图:以线段为边作正五边形和正三角形 , 连接 , 交于点 , 下列四位同学的说法错误的是( )
甲 乙 是的垂直平分线
丙 是等腰三角形
丁 与平行
A、甲 B、乙 C、丙 D、丁15. 表示不超过的最大整数.如 , , . 则下列结论:①;②若 , 则的取值范围是;③当时,的值为1或2;④是方程的唯一一个解.其中正确的结论是( )A、①② B、②④ C、②③ D、①③16. 课堂上,老师给出一道题:如图,将抛物线C:y=x2-6x+5在x轴下方的图象沿x轴翻折,翻折后得到的图象与抛物线C在x轴上方的图象记为G,已知直线l:y=x+m与图象G有两个公共点,求m的取值范围甲同学的结果是-5<m<-1,乙同学的结果是m> . 下列说法正确的是( ) A、甲的结果正确 B、乙的结果正确 C、甲、乙的结果合在一起才正确 D、甲、乙的结果合在一起也错误
A、甲的结果正确 B、乙的结果正确 C、甲、乙的结果合在一起才正确 D、甲、乙的结果合在一起也错误二、填空题
-
17. 若 , 则的值为 .18. 嘉琪准备完成题目:解一元二次方程 . 若“□”表示一个字母,且一元二次方程有实数根,则“”的最大值为 , 此时方程的解为 .19. 如图,经过原点的直线与反比例函数()的图象交于 , 两点(点在第一象限),点 , , 在反比例函数()的图象上,轴,轴,五边形的面积为56,四边形的面积为32.
 (1)、连接 , 则的面积为;(2)、 , .
(1)、连接 , 则的面积为;(2)、 , .三、解答题
-
20. 如图①是由8个同样大小的立方体组成的魔方,体积为8.

 (1)、求出这个魔方的棱长;(2)、图①中阴影部分是一个正方形 , 求出阴影部分的面积及其边长.(3)、把正方形放到数轴上,如图②,使得点与-1重合,那么点在数轴上表示的数为 .21. 当时,求的值.(1)、一位同学认为这道题无法求出代数式的值,他的具体做法如下:
(1)、求出这个魔方的棱长;(2)、图①中阴影部分是一个正方形 , 求出阴影部分的面积及其边长.(3)、把正方形放到数轴上,如图②,使得点与-1重合,那么点在数轴上表示的数为 .21. 当时,求的值.(1)、一位同学认为这道题无法求出代数式的值,他的具体做法如下:原式①
. ②
你认为第步开始出现错误.
(2)、请你写出正确的解题过程.22. 一个不透明的袋子中装有4个质地大小均相同的小球,这些小球分别标有数字4、5、6、 . 甲、乙两人每次同时从袋中各随机摸出1个小球,并计算摸出的这2个小球上的数字之和,记录后都将小球放回袋中搅匀,进行重复试验.试验数据如下表:摸球总次数
10
20
30
60
90
120
180
240
330
450
“和为10”出现的频数
2
10
13
24
30
37
58
82
110
150
“和为10”出现的频率
0.20
0.50
0.43
0.40
0.33
0.31
0.32
0.34
0.33
0.33
解答下列问题:
(1)、如果试验继续进行下去,根据上表数据,出现“和为10”的频率趋于稳定.请估计出现“和为10”的概率是 .(2)、如果摸出的这两个小球上数字之和为11的概率是 , 那么的值可以取8吗?请用列表法或画树状图法说明理由;如果的值不可以取8,请写出一个符合要求的值.23. 如图1,在中, , 为线段上一点,以为圆心,长为半径的圆与边 , 分别交于 , 两点,过点作的切线,交于点. (1)、求证: .(2)、如图2,若为的中点.
(1)、求证: .(2)、如图2,若为的中点.①探究与的数量关系,并说明理由;
②连接 , 若 , , 求阴影部分的面积.
24. 如图,在平面直角坐标系中,直线过点 , 点 , 直线:与轴交于点 .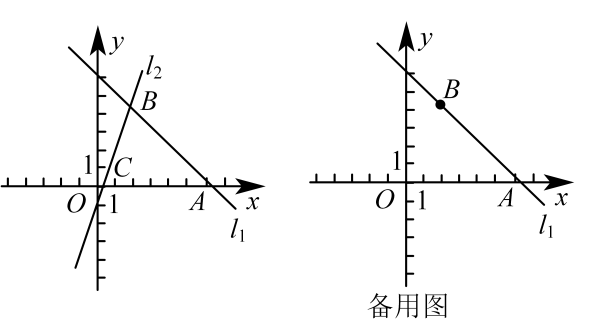 (1)、求直线的函数表达式.(2)、若直线过点 .
(1)、求直线的函数表达式.(2)、若直线过点 .①求的值.
②若点在内部,求的取值范围.
(3)、直线与直线和直线分别交于点、 , 当线段的长不大于4时,求的取值范围.25. 建大棚种植蔬菜是农民致富的一条好途径.经市场调查发现:搭建一个面积为(为整数)公顷的大棚,前期准备所需总费用由建设费用和内部设备费用两部分组成,其中建设费用与成正比例,内部设备费用与成正比例,部分数据如下:大棚面积/公顷
3
8
前期准备所需总费用/万元
21
134
(1)、求前期准备所需总费用与之间的函数关系式.(2)、若种植1公顷蔬菜需种子、化肥、农药的开支0.4万元,收获1公顷的蔬菜年均可卖9.4万元.设当年收获蔬菜的总收益(扣除修建和种植成本)为万元,写出与之间的函数关系式.(3)、求种植的面积为多少公顷时,当年收获蔬菜的总收益最大,最大值为多少?26. 在中, , . 点在线段上运动(不与点、重合).如图1,连接 , 作 , 与交于点 . (1)、求证: .(2)、若 , 当为多少度时, 是等腰三角形?(3)、如图2,当点运动到中点时,点在的延长线上,连接 , , 点在线段上,连接 .
(1)、求证: .(2)、若 , 当为多少度时, 是等腰三角形?(3)、如图2,当点运动到中点时,点在的延长线上,连接 , , 点在线段上,连接 .①与是否相似?请说明理由.
②设 , 的面积为S,试用含的代数式表示S.