河北省保定市高碑店2023年中考模拟统考数学试卷
试卷更新日期:2023-05-05 类型:中考模拟
一、单选题
-
1. 下列各数中,比小的数是( )A、0 B、 C、-1 D、12. 如图,∠AOB的大小为( )
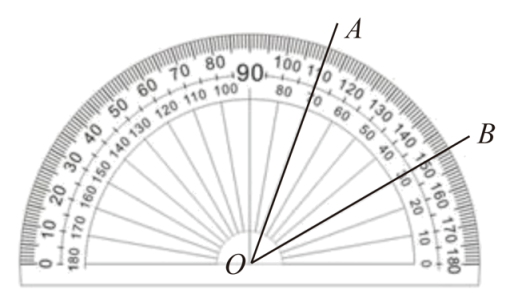 A、 B、 C、 D、3. 可以表示为( )A、 B、 C、 D、4. 小化将一张如图所示的矩形纸片沿对角线剪开,他利用所得的两个直角三角形进行图形变换,构成了下列四个图形,这四个图形中不是轴对称图形的是( )
A、 B、 C、 D、3. 可以表示为( )A、 B、 C、 D、4. 小化将一张如图所示的矩形纸片沿对角线剪开,他利用所得的两个直角三角形进行图形变换,构成了下列四个图形,这四个图形中不是轴对称图形的是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 将化为最简得到 , 那么的值是( )A、8 B、9 C、12 D、276. 从某个方向上看如图1所示的几何体,若得到的视图是图2,则这个方向是( )
5. 将化为最简得到 , 那么的值是( )A、8 B、9 C、12 D、276. 从某个方向上看如图1所示的几何体,若得到的视图是图2,则这个方向是( ) A、上面 B、左面 C、上面或正面 D、左面或正面7. 下面是投影屏上出示的抢答题,需要回答横线上符号所代表的内容,则下列回答错误的是( )
A、上面 B、左面 C、上面或正面 D、左面或正面7. 下面是投影屏上出示的抢答题,需要回答横线上符号所代表的内容,则下列回答错误的是( )如图, , , 平分 , , 求的度数.解: ,
.
平分 ,
█.
,
◆,
, ,
▲.
 A、※代表 B、█代表 C、◆代表 D、▲代表8. 将的计算结果用科学记数法表示为( )A、 B、 C、 D、9. 如图为东西流向且河岸平行的一段河道,点 , 分别为两岸上一点,且点 在点 正北方向,由点 向正东方向走 米到达点 ,此时测得点 在点 的北偏西55°方向上,则河宽 的长为( )
A、※代表 B、█代表 C、◆代表 D、▲代表8. 将的计算结果用科学记数法表示为( )A、 B、 C、 D、9. 如图为东西流向且河岸平行的一段河道,点 , 分别为两岸上一点,且点 在点 正北方向,由点 向正东方向走 米到达点 ,此时测得点 在点 的北偏西55°方向上,则河宽 的长为( ) A、 米 B、 米 C、 米 D、 米10. 有一个从袋子中摸球的游戏,小红根据游戏规则作出了如图所示的树状图,则此次摸球的游戏规则是( )
A、 米 B、 米 C、 米 D、 米10. 有一个从袋子中摸球的游戏,小红根据游戏规则作出了如图所示的树状图,则此次摸球的游戏规则是( ) A、随机摸出一个球后放回,再随机摸出1个球 B、随机摸出一个球后不放回,再随机摸出1个球 C、随机摸出一个球后放回,再随机摸出2个球 D、随机摸出一个球后不放回,再随机摸出2个球11. 如图,在一张正六边形纸片中剪下两个全等的直角三角形(阴影部分),拼成一个四边形,若拼成的四边形的面积为2,则纸片的剩余部分拼成的五边形的面积为( )
A、随机摸出一个球后放回,再随机摸出1个球 B、随机摸出一个球后不放回,再随机摸出1个球 C、随机摸出一个球后放回,再随机摸出2个球 D、随机摸出一个球后不放回,再随机摸出2个球11. 如图,在一张正六边形纸片中剪下两个全等的直角三角形(阴影部分),拼成一个四边形,若拼成的四边形的面积为2,则纸片的剩余部分拼成的五边形的面积为( ) A、5 B、6 C、8 D、1012. 分式的值可能等于( )A、0 B、1 C、2 D、13. 如图,四边形中,与不平行, , 分别是、的中点, , , 则的长可能是( )
A、5 B、6 C、8 D、1012. 分式的值可能等于( )A、0 B、1 C、2 D、13. 如图,四边形中,与不平行, , 分别是、的中点, , , 则的长可能是( ) A、4 B、6 C、8 D、1014. 已知关于x的一元二次方程2x2−(m+n)x+mn=0,其中m,n在数轴上的对应点如图所示,则这个方程的根的情况是( )
A、4 B、6 C、8 D、1014. 已知关于x的一元二次方程2x2−(m+n)x+mn=0,其中m,n在数轴上的对应点如图所示,则这个方程的根的情况是( ) A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定15. 如图,是的外接圆,在弧上找一点M,使点M平分弧 . 以下是甲乙丙三种不同的作法:
A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定15. 如图,是的外接圆,在弧上找一点M,使点M平分弧 . 以下是甲乙丙三种不同的作法:
作法正确的个数是( )
A、0个 B、1个 C、2个 D、3个16. 如图,把两块全等的直角三角板和叠放在一起,使三角板的锐角顶点与三角板的斜边中点重合,经过点 , 其中 , , , 把三角板固定不动,让三角板绕点逆时针旋转,旋转角为 . 其中 . 设射线与射线相交于点 , 线段与线段相交于点 . 给出下面三个结论:①;②的值不变,为8;③当时,设 , 两块三角板重叠部分的面积为 . 其中正确的是( )
 A、只有①与② B、只有①与③ C、只有②与③ D、①②③
A、只有①与② B、只有①与③ C、只有②与③ D、①②③二、填空题
-
17. 若单项式与的和是单项式,则 .18. 如图,用铁丝折成一个四边形ABCD(点C在直线BD的上方),且∠A=70°,∠BCD=120°,若使∠ABC、∠ADC平分线的夹角∠E的度数为100°,可保持∠A不变,将∠BCD (填“增大”或“减小”)°.
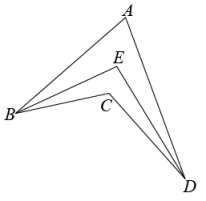 19. 如图,在平面直角坐标系中,反比例函数的图象经过点 , , 过点作轴的垂线,垂足为 , 连接 .
19. 如图,在平面直角坐标系中,反比例函数的图象经过点 , , 过点作轴的垂线,垂足为 , 连接 . (1)、该反比例函数的解析式为;(2)、当的面积为4时,点的坐标为 .(3)、在(2)的情况下,直线过线段上一点 , 的取值范围为 .
(1)、该反比例函数的解析式为;(2)、当的面积为4时,点的坐标为 .(3)、在(2)的情况下,直线过线段上一点 , 的取值范围为 .三、解答题
-
20. 已知P=A·B-M.(1)、若A=(-3)0 , B= , M=|-1|,求P的值;(2)、若A=3,B=x,M=5x-1,且P≤3,求x的取值范围,并在如图所示的数轴上表示出解集.
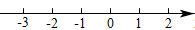 21. 定义:对于一个三位正整数,如果十位数字恰好等于百位数字与个位数字之和的一半,我们称这个三位正整数为“半和数”.
21. 定义:对于一个三位正整数,如果十位数字恰好等于百位数字与个位数字之和的一半,我们称这个三位正整数为“半和数”.例如,三位正整数234,因为 , 所以234是“半和数”.
(1)、判断147是否为“半和数”,并说明理由;(2)、小林列举了几个“半和数”:111、123、234、840…,并且她发现: , , , …,所以她猜测任意一个“半和数”都能被3整除.小林的猜想正确吗?若正确,请你帮小林说明该猜想的正确性;若错误,说明理由.22. 一枚质地均匀的正方体骰子如图1,六个面分别刻有1,2,3,4,5,6个点,A,B,C,D,E五名学生,每人随机投掷这枚骰子5次,投掷结束后,将每次掷出的骰子朝上面的点数求和.根据他们各自累积求和的结果绘制成如图2所示的不完整的条形统计图.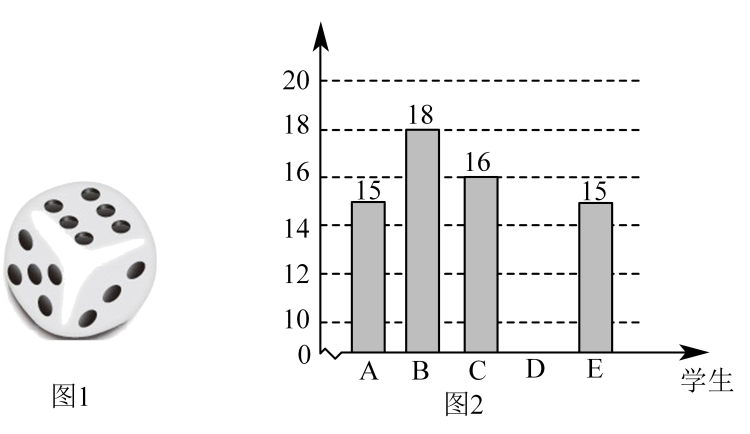 (1)、E同学连续投掷五次正方体骰子,掷得点数为4的频率为 , 求他这五次投掷的点数(不考虑投掷顺序);(2)、已知这五名学生各自累积求和的结果的平均数为17,
(1)、E同学连续投掷五次正方体骰子,掷得点数为4的频率为 , 求他这五次投掷的点数(不考虑投掷顺序);(2)、已知这五名学生各自累积求和的结果的平均数为17,①补全条形统计图;
②若D同学五次投掷的点数中,唯一众数是3且不为中位数,求D同学五次投掷的点数的中位数.
23. 如图,抛物线经过点A,B,C,点A的坐标为 . (1)、求抛物线的解析式和顶点坐标;(2)、当时,求y的最大值与最小值的差;(3)、若点P的坐标为 , 连接 , 并将线段向上平移个单位得到线段 , 若线段与抛物线只有一个交点,请直接写出a的取值范围.24. 如图,点O在射线AP上, , 以点O为圆心,AO长为半径作半圆O,交AP于点B.点C在上,点D在射线BP上,且 , 作射线交于点E.
(1)、求抛物线的解析式和顶点坐标;(2)、当时,求y的最大值与最小值的差;(3)、若点P的坐标为 , 连接 , 并将线段向上平移个单位得到线段 , 若线段与抛物线只有一个交点,请直接写出a的取值范围.24. 如图,点O在射线AP上, , 以点O为圆心,AO长为半径作半圆O,交AP于点B.点C在上,点D在射线BP上,且 , 作射线交于点E. (1)、若为半圆O的切线,求的度数;(2)、连接AE,若 , 求证:;(3)、若的长为 , 求的长.25. 某超市经营的A和B两种啇品的信息如下:
(1)、若为半圆O的切线,求的度数;(2)、连接AE,若 , 求证:;(3)、若的长为 , 求的长.25. 某超市经营的A和B两种啇品的信息如下:商品
A
B
规格(千克/箱)
12
15
进价(元/箱)
60
150
(1)、已知今年2~5月这四个月销售A和B共3300千克,获得利润共10800元,A比B多销售了300千克,B的销售单价比A的销售单价多10元/千克,求这四个月销售A,B各多少千克、销售单价各是多少元/千克、(利润售价进价)(2)、根据之前的销售情况,的新品6月上市,5月底要进6月要卖的货时,发现的进价下降到54元/箱,超市为了保持与之前相同的利润,所以将A的售价也下调了、B的新品11月才能上市,进价没有改变,超市保持售价也不变,估计今年6月到10月这五个月,还能销售A和B共3600千克,其中,A的销售量不低于2100千克.假设这五个月,A销售了千克,销售A和B获得的总利润为元、求出与之间的函数关系式,并求这五个月最多可获得总利润多少元.26. 如图,矩形ABCD中,AB=4,AD=3,点E在射线CB上运动(可与点C重合),DE的中点为G,将EG绕点E顺时针旋转90°得到EF,再以ED,EF为一组邻边作矩形DEFH. (1)、当点E为BC的中点时,点F到直线BC的距离为;(2)、当点F落在矩形ABCD的边(或边所在的直线)上时,求CE的长;(3)、点E在线段BC(可与点B,C重合)上运动时,直接写出线段CF的最小值.
(1)、当点E为BC的中点时,点F到直线BC的距离为;(2)、当点F落在矩形ABCD的边(或边所在的直线)上时,求CE的长;(3)、点E在线段BC(可与点B,C重合)上运动时,直接写出线段CF的最小值.