广东省深圳市2023年三十校联考中考质检数学试卷（2月份）

试卷更新日期：2023-05-05 类型：中考模拟

进入出卷网下载

一、单选题

1. 某物体如图所示，它的主视图是（）

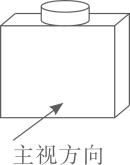A、 B、 C、 D、

查看试题解析
2. 在一个不透明的口袋中装有4个红球和若干个白球，他们除颜色外其他完全相同．通过多次摸球实验后发现，摸到红球的频率稳定在25%附近，则口袋中白球可能有（）

A、6个 B、15个 C、13个 D、12个

查看试题解析
3. $x = 1$ 是关于 $x$ 的一元二次方程 $x^{2} + a x + 2 b = 0$ 的解，则 $2 a + 4 b =$ （）

A、-2 B、-3 C、4 D、-6

查看试题解析
4. 在Rt△ABC中，∠C=90°，BC=5，AC=12，则sinB的值是（）

A、 $\frac{5}{12}$ B、 $\frac{12}{5}$ C、 $\frac{5}{13}$ D、 $\frac{12}{13}$

查看试题解析
5. 受国际油价影响，今年我国汽油价格总体呈上升趋势．某地92号汽油价格三月底是6.2元/升，五月底是8.9元/升．设该地92号汽油价格这两个月平均每月的增长率为 $x$ ，根据题意列出方程，正确的是（）

A、 $6.2 (1 + x)^{2} = 8.9$ B、 $8.9 (1 + x)^{2} = 6.2$ C、 $6.2 (1 + x^{2}) = 8.9$ D、 $6.2 (1 + x) + 6.2 (1 + x)^{2} = 8.9$

查看试题解析
6. 如图，以点O为位似中心，作四边形 $A B C D$ 的位似图形 $A^{'} B^{'} C^{'} D^{'}$ ，已知 $\frac{O A}{O A^{'}} = \frac{1}{3}$ ，若四边形 $A B C D$ 的面积是2，则四边形 $A^{'} B^{'} C^{'} D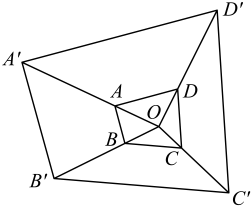^{'}$ 的面积是（）

A、4 B、6 C、16 D、18

查看试题解析
7. 下列命题中假命题是（）

A、二次函数 $y = x^{2} - 2 x - 1$ 的对称轴是直线 $x = 1$ B、对角线垂直且相等的四边形是正方形 C、某双曲线经过点 $(1 ， 2)$ ，则必过点 $(2 ， 1)$ D、方程 $x^{2} - x + 1 = 0$ 无实数根

查看试题解析
8. 数学中余弦定理是这样描述的：在 $△ A B C$ 中， $∠ A$ 、 $∠ B$ 、 $∠ C$ 所对的边分别为 $a$ 、 $b$ 、 $c$ ，则三角形中任意一边的平方等于另外两边的平方和减去这两边及这两边的夹角的余弦值的乘积的2倍，用公式可描述为： $a^{2} = b^{2} + c^{2} - 2 b c c o s A$ ， $b^{2} = a^{2} + c^{2} - 2 a c c o s B$ ， $c^{2} = a^{2} + b^{2} - 2 a b c o s C$ ．在 $△ A B C$ 中， $A B = 3$ ， $A C = 4$ ， $∠ A = 60 °$ ，则 $B C$ 的值是（）

A、5 B、 $\sqrt{14}$ C、 $\sqrt{13}$ D、2

查看试题解析
9. 二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，以下结论正确的个数为（）
① $a b c < 0$ ；② $c + 2 a < 0$ ；③ $9 a - 3 b + c = 0$ ；④ $a m^{2} - a + b m + b > 0$ （ $m$ 为任意实数）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图， $∠ A B C = ∠ A D B = 90 °$ ， $D A = D B$ ，若 $B C = 2$ ， $A B = 4$ ，则点 $D$ 到 $A C$ 的距离是（）

A、 $\frac{5 \sqrt{5}}{6}$ B、 $\frac{6 \sqrt{5}}{5}$ C、 $\frac{4 \sqrt{5}}{5}$ D、 $\frac{5 \sqrt{5}}{4}$

查看试题解析

二、填空题

11. 若 $\frac{y}{x} = \frac{3}{7}$ ，则 $\frac{x - y}{x} =$ ．

查看试题解析
12. 抛物线 $y = x^{2} - 2 x + 3$ 向右平移2个单位长度，再向上平移3个单位长度，得到抛物线的顶点坐标是．

查看试题解析
13. 如图，在矩形 $A B C D$ 中，作 $B D$ 的垂直平分线分别与 $A D 、 B C$ 交于点M、N，连接 $B M 、 D N$ ．若 $B M = 5 ， N C = 3$ ．则矩形 $A B C D$ 的周长为．

查看试题解析
14. 如图， $O A = 8 ， A B = 6$ ，将 $△ A B O$ 向右平移到 $△ C D E$ 位置，A的对应点是C，O的对应点是E，反比例函数 $y = \frac{k}{x}$ 的图象经过点C和 $D E$ 的中点F，则k的值是．

查看试题解析
15. 如图， $△ A B C$ 与 $△ A E D$ 都是等腰三角形， $∠ A B C = ∠ A E D = 120 °$ ，点P为 $A C$ 边上一点，且 $P A = m$ ， $P B$ 与 $B A$ 所夹锐角为 $∠ P B A = β$ ，点E为 $P B$ 上一动点，求点E自点B运动至点P时，点D所经过的路径长．（用含β与m的式子表示）

查看试题解析

三、解答题

16. 计算： ${(4 - \sqrt{3})}^{0} - 3 \tan 60 ° - {(- \frac{1}{2})}^{- 1} + \sqrt{12}$ .

查看试题解析
17. 2022年4月15日是第七个全民国家安全教育日，某校七、八年级举行了一次国家安全知识竞赛，经过评比后，七年级的两名学生（用 $A$ ， $B$ 表示）和八年级的两名学生（用 $C$ ， $D$ 表示）获得优秀奖．

(1)、从获得优秀奖的学生中随机抽取一名分享经验，恰好抽到七年级学生的概率是．

(2)、从获得优秀奖的学生中随机抽取两名分享经验，请用列表法或画树状图法，求抽取的两名学生恰好一名来自七年级、一名来自八年级的概率．

查看试题解析
18. 小明学了《解直角三角形》内容后，对一条东西走向的隧道 $A B$ 进行实地测量．如图所示，他在地面上点C处测得隧道一端点A在他的北偏东 $15 °$ 方向上，他沿西北方向前进 $100 \sqrt{3}$ 米后到达点D，此时测得点A在他的东北方向上，端点B在他的北偏西 $60 °$ 方向上，（点A、B、C、D在同一平面内）

(1)、求点D与点A的距离；

(2)、求隧道 $A B$ 的长度．（结果保留根号）

查看试题解析
19. 小欣研究了函数 $y = \frac{1}{x + 1}$ 的图象与性质，其研究过程如下：

(1)、绘制函数图象①列表：下表是 $x$ 与 $y$ 的几组对应值，其中 $m =$ ▲ ；
$x$
…
-4
-3
-2
$- \frac{3}{2}$
$- \frac{4}{3}$
$- \frac{2}{3}$
$- \frac{1}{2}$
0
1
2
…
$y$
…
$- \frac{1}{3}$
$- \frac{1}{2}$
-1
-2
-3
3
2
$m$
$\frac{1}{2}$
$\frac{1}{3}$
…
②描点：根据表中的数值描点 $(x ， y)$ ；③连线：用平滑的曲线顺次连接各点，请把图象补充完整．

(2)、探究函数性质：下列说法错误的是（）

A、函数值 $y$ 随 $x$ 的增大而减小 B、函数图象不经过第四象限． C、函数图象与直线 $x = - 1$ 没有交点 D、函数图象对称中心 $(- 1 ， 0)$

(3)、如果点 $A (x_{1} ， y_{1})$ 、 $B (x_{2} ， y_{2})$ 在函数图象上，如果 $x_{1} + x_{2} = - 2$ ，则 $y_{1} + y_{2} =$ ．

查看试题解析
20. 如图，已知菱形 $A B C D$ ，点E是 $B C$ 上的点，连接 $D E$ ，将 $△ C D E$ 沿 $D E$ 翻折，点C恰好落在边 $A B$ 上的F点上，连接 $D F$ ，延长 $F E$ ，交 $D C$ 延长线于点G．

(1)、求证： $△ D F G \sim △ F A D$ ；

(2)、若菱形 $A B C D$ 的边长为5， $A F = 3$ ，求 $B E$ 的长．

查看试题解析
21. 在平面直角坐标系中，如果一个点的横坐标与纵坐标相等，则称该点为“不动点”
例如 $(- 3 ， - 3)$ 、 $(1 ， 1)$ 、 $(2023 ， 2023)$ 都是“不动点”，已知双曲线 $y = \frac{9}{x}$

(1)、下列说法错误的是（）

A、直线 $y = x$ 的图象上有无数个“不动点” B、函数 $y = \frac{- 1}{x}$ 的图象上没有“不动点” C、直线 $y = x + 1$ 的图象上有无数个“不动点” D、函数 $y = x^{2}$ 的图象上有两个“不动点”

(2)、求双曲线 $y = \frac{9}{x}$ 上的“不动点”；

(3)、若抛物线 $y = a x^{2} - 3 x + c$ （ $a$ 、 $c$ 为常数）上有且只有一个“不动点”，
①当 $a > 1$ 时，求 $c$ 的取值范围．
②如果 $a = 1$ ，过双曲线 $y = \frac{9}{x}$ 图象上第一象限的“不动点”作平行于 $x$ 轴的直线 $l$ ，若抛物线上有四个点到 $l$ 的距离为 $m$ ，直接写出 $m$ 的取值范围．

查看试题解析
22. 如图

(1)、如图1， $R t △ A B C$ 中， $∠ C = 90 ° ， A B = 10 ， A C = 8$ ， E是 $A C$ 上一点， $A E = 5 ， E D ⊥ A B$ ，垂足为D，求 $A D$ 的长．

(2)、类比探究：如图2， $△ A B C$ 中， $A C = 14 ， B C = 6$ ，点D，E分别在线段 $A B ， A C$ 上， $∠ E D B = ∠ A C B = 60 ° ， D E = 2$ ．求 $A D$ 的长．

(3)、拓展延伸：如图3， $△ A B C$ 中，点D，点E分别在线段 $A B ， A C$ 上， $∠ E D B = ∠ A C B = 60 °$ ．延长 $D E ， B C$ 交于点F， $A D = 4 ， D E = 5 ， E F = 6 ， D E < B D$ ， $\frac{B C}{A C} =$ ； $B D =$ ．

查看试题解析

$x$	…	-4	-3	-2	$- \frac{3}{2}$	$- \frac{4}{3}$	$- \frac{2}{3}$	$- \frac{1}{2}$	0	1	2	…
$y$	…	$- \frac{1}{3}$	$- \frac{1}{2}$	-1	-2	-3	3	2	$m$	$\frac{1}{2}$	$\frac{1}{3}$	…