安徽省芜湖市无为市2023年中考二模数学试题
试卷更新日期:2023-05-05 类型:中考模拟
一、单选题
-
1. 下列实数中最小的是( )A、1 B、 C、-4 D、02. 下列运算正确的是( )A、(﹣a2)3=﹣a5 B、a3•a5=a15 C、(﹣a2b3)2=a4b6 D、3a2﹣2a2=13. 如图,桌面上有一个一次性纸杯,它的正视图应是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 新冠疫情在我国得到了很好地控制,可至今仍在海外肆虐,截止2021年3月底,海外累计确诊128924229人,128924229用科学记数法可表示为(精确到千万位)( )A、 B、 C、 D、5. 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=40°,那么∠2的度数是( )
4. 新冠疫情在我国得到了很好地控制,可至今仍在海外肆虐,截止2021年3月底,海外累计确诊128924229人,128924229用科学记数法可表示为(精确到千万位)( )A、 B、 C、 D、5. 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=40°,那么∠2的度数是( ) A、35° B、45° C、50° D、65°6. 为了调查八年级学生完成家庭作业所需的时间,在某校抽查了8名学生,他们每天完成作业所需的时间分别为(单位:分):70,75,90,70,70,58,80,55,则这组数据的众数、中位数、平均数依次是( )A、70,70,71; B、70,71,70; C、71,70,70; D、70,70,707. 关于x的一元二次方程kx2+3x﹣1=0有实数根,则k的取值范围是( )A、k≤﹣ B、k≤﹣ 且k≠0 C、k≥﹣ D、k≥﹣ 且k≠08. 已知圆锥的底面半径为50cm,母线长为80cm,则此圆锥的侧面积为( )A、4000πcm2 B、3600πcm2 C、2000 πcm2 D、1000πcm29. 如图,在正方形ABCD中,已知边长 , 点E是BC边上一动点(点E不与B、C重合),连接AE,作点B关于直线AE的对称点F,则线段CF的最小值为( )
A、35° B、45° C、50° D、65°6. 为了调查八年级学生完成家庭作业所需的时间,在某校抽查了8名学生,他们每天完成作业所需的时间分别为(单位:分):70,75,90,70,70,58,80,55,则这组数据的众数、中位数、平均数依次是( )A、70,70,71; B、70,71,70; C、71,70,70; D、70,70,707. 关于x的一元二次方程kx2+3x﹣1=0有实数根,则k的取值范围是( )A、k≤﹣ B、k≤﹣ 且k≠0 C、k≥﹣ D、k≥﹣ 且k≠08. 已知圆锥的底面半径为50cm,母线长为80cm,则此圆锥的侧面积为( )A、4000πcm2 B、3600πcm2 C、2000 πcm2 D、1000πcm29. 如图,在正方形ABCD中,已知边长 , 点E是BC边上一动点(点E不与B、C重合),连接AE,作点B关于直线AE的对称点F,则线段CF的最小值为( ) A、5 B、 C、 D、10. 如图所示是抛物线的部分图象,其顶点坐标为 , 且与x轴的一个交点在点和之间,则下列结论:①;②;③;④一元二次方程没有实数根.其中正确的结论个数是( )
A、5 B、 C、 D、10. 如图所示是抛物线的部分图象,其顶点坐标为 , 且与x轴的一个交点在点和之间,则下列结论:①;②;③;④一元二次方程没有实数根.其中正确的结论个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
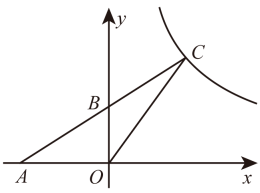
11. 函数的自变量的取值范围是 .12. 分解因式: .13. 如图,点在轴的负半轴上,点在反比例函数()的图象上,交轴于点 , 若点是的中点,的面积为 , 则的值为 .
 14. 已知四边形是矩形, , , 为边上一动点且不与、重合,连接 , 如图,过点作交于点 .
14. 已知四边形是矩形, , , 为边上一动点且不与、重合,连接 , 如图,过点作交于点 .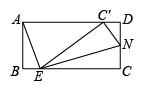
①若 , 那么的长;
②将沿翻折,点的对应点恰好落在边上,那么的长 .
三、解答题
-
15. 计算: .16. 《孙子算经》是我国古代重要的数学著作,其中有如下问题:今有人盗库绢,不知所失几何,但闻草中分绢,人得六匹,盈六匹;人得七匹,不足七匹.问人、绢各几何?大意是:有几个盗贼偷了仓库里的绢,不知道具体偷盗了多少匹绢,只听盗贼在草丛中分绢时说:“每人分6匹,会剩下6匹;每人分7匹,还差7匹.”问有多少盗贼?多少匹绢?17. 如图,在平面直角坐标系中,的三个顶点 , , 均在正方形网格的格点上.

⑴画出将沿轴方向向右平移5个单位长度后得到的;
⑵画出关于轴的对称图形 , 并直接写出点的坐标;
⑶在轴上找一点 , 使得的值最小.(保留作图痕迹)
18. 细心观察如图,认真分析各式,然后解答问题., ,
, ,
, ,
……
 (1)、;(2)、用含(是正整数)的等式表示上述面积变化规律: , ;(3)、若一个三角形的面积是 , 则它是第个三角形;(4)、求出的值.19. 为巩固农村脱贫成果,利兴村委会计划利用一块如图所示的空地 , 培育绿植销售,空地南北边界 , 西边界 , 经测量得到如下数据,点A在点C的北偏东方向,在点D的北偏东方向,米,求空地南北边界和的长(结果保留整数,参考数据: , ).
(1)、;(2)、用含(是正整数)的等式表示上述面积变化规律: , ;(3)、若一个三角形的面积是 , 则它是第个三角形;(4)、求出的值.19. 为巩固农村脱贫成果,利兴村委会计划利用一块如图所示的空地 , 培育绿植销售,空地南北边界 , 西边界 , 经测量得到如下数据,点A在点C的北偏东方向,在点D的北偏东方向,米,求空地南北边界和的长(结果保留整数,参考数据: , ).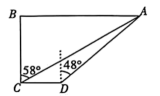 20. 如图,点E是的内心,AE的延长线和的外接圆相交于点D,与弦BC交于点F.
20. 如图,点E是的内心,AE的延长线和的外接圆相交于点D,与弦BC交于点F. (1)、求证: .(2)、若 , , 求AE的长.21. 为了解某次数学考试情况,随机抽取了部分学生的成绩(得分均为整数,满分为150分),并将成绩分组如下:第一组(75≤x<90)、第二组(90≤x<105)、第三组(105≤x<120)、第四组(120≤x<135)、第五组(135≤x≤150).并将成绩绘制成如下频数分布直方图和扇形统计图(不完整),根据图中信息,回答下列问题:
(1)、求证: .(2)、若 , , 求AE的长.21. 为了解某次数学考试情况,随机抽取了部分学生的成绩(得分均为整数,满分为150分),并将成绩分组如下:第一组(75≤x<90)、第二组(90≤x<105)、第三组(105≤x<120)、第四组(120≤x<135)、第五组(135≤x≤150).并将成绩绘制成如下频数分布直方图和扇形统计图(不完整),根据图中信息,回答下列问题: (1)、本次调查共随机抽取了名学生,并将频数分布直方图补充完整;(2)、该年级共有1500名考生,估计成绩120分以上(含120分)学生有名;(3)、如果第一组(75≤x<90)中只有一名是女生,第五组(135≤x≤150)中只有一名是男生,现从第一组、第五组分别随机选出一名同学谈答题感想,试求所选两名学生刚好是一名女生和一名男生的概率.22. 如图,已知抛物线与轴交于、两点,与轴交于点 , 且点的坐标为 , 直线经过点、 .
(1)、本次调查共随机抽取了名学生,并将频数分布直方图补充完整;(2)、该年级共有1500名考生,估计成绩120分以上(含120分)学生有名;(3)、如果第一组(75≤x<90)中只有一名是女生,第五组(135≤x≤150)中只有一名是男生,现从第一组、第五组分别随机选出一名同学谈答题感想,试求所选两名学生刚好是一名女生和一名男生的概率.22. 如图,已知抛物线与轴交于、两点,与轴交于点 , 且点的坐标为 , 直线经过点、 . (1)、抛物线解析式为 , 直线解析式为;(2)、点是第一象限内抛物线上的一个动点与点 , 不重合 , 过点作轴于点 , 交直线于点 , 连接 , 设点的横坐标为 , 的面积为 , 求关于的函数解析式及自变量的取值范围,并求出的最大值;(3)、已知点为抛物线对称轴上的一个动点,若是以为直角边的直角三角形,请直接写出点的坐标.23. 通过以前的学习,我们知道:“如图1,在正方形中, , 则”. 某数学兴趣小组在完成了以上学习后,决定对该问题进一步探究:
(1)、抛物线解析式为 , 直线解析式为;(2)、点是第一象限内抛物线上的一个动点与点 , 不重合 , 过点作轴于点 , 交直线于点 , 连接 , 设点的横坐标为 , 的面积为 , 求关于的函数解析式及自变量的取值范围,并求出的最大值;(3)、已知点为抛物线对称轴上的一个动点,若是以为直角边的直角三角形,请直接写出点的坐标.23. 通过以前的学习,我们知道:“如图1,在正方形中, , 则”. 某数学兴趣小组在完成了以上学习后,决定对该问题进一步探究: (1)、【问题探究】如图2,在正方形中,点 , , , 分别在线段 , , , 上,且 , 试猜想;(2)、【知识迁移】如图3,在矩形中, , , 点 , , , 分别在线段 , , , 上,且 , 试猜想的值,并证明你的猜想;(3)、【拓展应用】如图4,在四边形中, , , , 点 , 分别在线段 , 上,且 , 求的值.
(1)、【问题探究】如图2,在正方形中,点 , , , 分别在线段 , , , 上,且 , 试猜想;(2)、【知识迁移】如图3,在矩形中, , , 点 , , , 分别在线段 , , , 上,且 , 试猜想的值,并证明你的猜想;(3)、【拓展应用】如图4,在四边形中, , , , 点 , 分别在线段 , 上,且 , 求的值.