安徽省黄山地区2023年中考一模数学试题

试卷更新日期：2023-05-05 类型：中考模拟

进入出卷网下载

一、单选题

1. -3的绝对值是（）

A、3 B、-3 C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
2. 据统计，2023年我国人口数约为14亿4730万，其中4730万用科学记数法表示为（）

A、 $4.73 \times 1 0^{8}$ B、 $0.473 \times 1 0^{8}$ C、 $4.73 \times 1 0^{7}$ D、 $47.3 \times 1 0^{6}$

查看试题解析
3. 一个几何体的三视图如图所示，则这个几何体是（）

A、 B、 C、 D、

查看试题解析
4. 下列各式中计算正确的是（）

A、 $a^{3} + a^{2} = a^{5}$ B、 $a^{3} \div a^{2} = a$ C、 $a^{2} \cdot a^{3} = a^{6}$ D、 $(a^{3})^{2} = a^{5}$

查看试题解析
5. 将盛有凉牛奶的瓶子放在热水中(如图甲所示)，通过热传递方式改变牛奶的内能，图乙是凉牛奶与热水的温度随时间变化的图像．假设热水放出热量全部被牛奶吸收，下列回答错误的是（）

A、0 $∼$ 8min时，热水的温度随时间的增加逐渐降低； B、0 $∼$ 8min时，凉牛奶的温度随时间的增加逐渐上升； C、8min时，热水和凉牛奶的温度相同； D、0min时，两者的温度差为80 $° C$ ．

查看试题解析
6. 如图是一款手推车的平面示意图，其中 $A B ∥ C D$ ， $∠ 1 = 24 °$ ， $∠ 2 = 76 °$ ，则∠3的度数为（）

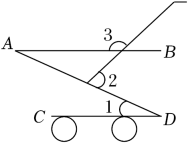A、104° B、128° C、138° D、156°

查看试题解析
7. 在⊙O中，P为其内一点，过点P的最长的弦为8cm，最短的弦长为4cm，则OP为．（）

A、2 $\sqrt{3}$ cm B、 $\sqrt{3}$ cm C、3cm D、2cm

查看试题解析
8. 在 $- 2 ， \sqrt{2} ， π ， 1.010010001 ⋯ ， \frac{1}{3}$ 这5个数中随机选择2个数，都是无理数的概率是（）

A、 $\frac{2}{5}$ B、 $\frac{3}{10}$ C、 $\frac{3}{5}$ D、 $\frac{1}{2}$

查看试题解析
9. 已知一次函数 $y = k x + 2$ 的图象经过点 $(- 1 ， y_{1}) ， (- 2 ， y_{2})$ ，且 $y_{1} > y_{2}$ ，则该一次函数的图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 在△ABC中，若O为BC边的中点，则必有：AB²+AC²=2AO²+2BO²成立.依据以上结论，解决如下问题：如图，在矩形DEFG中，已知DE=4，EF=3，点P在以DE为直径的半圆上运动，则PF²+PG²的最小值为（）

A、 $\sqrt{10}$ B、 $\frac{19}{2}$ C、34 D、10

查看试题解析

二、填空题

11. 不等式 $\frac{3 - x}{2} < 1$ 的解集为．

查看试题解析
12. 方程 $\frac{3}{x^{2} - 1} = \frac{1}{x - 1}$ 的解是．

查看试题解析
13. 如图，已知第一象限的双曲线与正方形 $O C A E$ 的两边相交于 $D$ 、 $B$ 两点，直线 $y = \frac{1}{3} x$ 过 $B$ 点．则 $D E ： A D$ 的值是．

查看试题解析
14. 如图，在矩形纸片 $A B C D$ 中， $A B = 3$ ， $B C = 4$ ，点E是边 $C D$ 上一点（不与点C、D重合），且 $C E$ 的长是整数，将纸片沿过点A的一条直线折叠，点B落在点 $B^{'}$ 处，折痕交 $B C$ 于点P，沿直线 $P E$ 再折叠纸片，点C落在 $C^{'}$ 处，且 $B^{'}$ 、 $C^{'}$ 、P三点共线．

(1)、 $∠ A P E$ 的度数；

(2)、线段 $B P$ 的长为；

查看试题解析

三、解答题

15. 计算： ${(\sqrt{2} - 1)}^{0} - \sqrt{16} + {(- \frac{1}{2})}^{- 2}$

查看试题解析
16. 如图，在边长为1个单位长度的10×10的小正方形网格中，点O和 $△ A B C$ 的顶点都在格点（网格线的交点）上．

(1)、作出 $△ A B C$ 关于点O对称的 $△ A^{'} B^{'} C^{'}$ ．

(2)、以线段 $A^{'} B^{'}$ 为一边，作出平行四边形 $A^{'} B^{'} P Q$ ，使得点P，Q都在格点上，且平行四边形 $A^{'} B^{'} P Q$ 的面积是15．（画出一个即可）

查看试题解析
17. 数字化阅读凭借其独有的便利性成为了更快获得优质内容的重要途径．近年来，我国数字阅读用户规模持续增长，据统计2020年我国数字阅读用户规模达4.94亿人，2022年约为5.9774亿人．

(1)、求2020年到2022年我国数字阅读用户规模的年平均增长率；

(2)、按照这个增长率，预计2023年我国数字阅读用户规模能否达到6.5亿人．

查看试题解析
18. 观察以下等式：
第1个等式： $4^{2} - 2^{2} = 3 \times 4$ ；
第2个等式： $6^{2} - 4^{2} = 5 \times 4$ ；
第3个等式： $8^{2} - 6^{2} = 7 \times 4$ ；
第4个等式： $1 0^{2} - 8^{2} = 9 \times 4$ ；
······
按照以上规律，解决下列问题：

(1)、写出第5个等式：；

(2)、写出你猜想的第 $n$ 个等式（用含 $n$ 的式子表示），并证明．

查看试题解析
19. 随着科技的发展，无人机已广泛应用于生产和生活，如代替人们在高空测量距离和角度.某校“综合与实践”活动小组的同学要测量 $A B$ ， $C D$ 两座楼之间的距离，他们借助无人机设计了如下测量方案：无人机在 $A B$ ， $C D$ 两楼之间上方的点 $O$ 处，点 $O$ 距地面 $A C$ 的高度为 $60 m$ ，此时观测到楼 $A B$ 底部点 $A$ 处的俯角为 $70 °$ ，楼 $C D$ 上点 $E$ 处的俯角为 $30 °$ ，沿水平方向由点 $O$ 飞行 $26 m$ 到达点 $F$ ，测得点 $E$ 处俯角为 $60 °$ ，其中点 $A$ ， $B$ ， $C$ ， $D$ ， $E$ ， $F$ ， $O$ 均在同一竖直平面内.请根据以上数据求楼 $A B$ 与 $C D$ 之间的距离 $A C$ 的长.（结果精确到 $1 m$ .参考数据： $s i n 70 ° \approx 0.94$ ， $c o s 70 ° \approx 0.34$ ， $t a n 70 ° \approx 2.75$ ， $\sqrt{3} \approx 1.73$ ）．

查看试题解析
20. 如图，在Rt $△$ ABC中， $∠ B A C = 90 °$ ， O是AB边上的一点，以OA为半径的⊙O与边BC相切于点E．

(1)、若 $A B = 8$ ， ⊙O的半径为3，求AC的长．

(2)、过点E作弦EF⊥AB于G，连接AF，若 $∠ A F E = 2 ∠ A B C$ ．求证：四边形ACEF是菱形．

查看试题解析
21. 垃圾分类是在源头将垃圾分类投放，并通过分类的清运和回收使之重新变成资源.某城市环保部门抽样调查了某居民小区一段时间内生活垃圾的分类情况，将获得的数据整理绘制成如下两幅不完整的统计图.（注： $A$ 为厨余垃圾， $B$ 为可回收垃圾， $C$ 为其它垃圾， $D$ 为有害垃圾）
根据统计图提供的信息，解答下列问题：

(1)、求这次抽样调查中可回收垃圾的吨数，并将条形统计图补充完整；

(2)、求扇形统计图中，“可回收垃圾”所对应的圆心角度数；

(3)、假设该城市每月产生的生活垃圾为12000吨，且全部分类处理，请估计每月产生的有害垃圾有多少吨？

查看试题解析
22. 如图，过等边 $Δ A B C$ 的顶点A作 $A C$ 的垂线 $l$ ，点 $P$ 为 $l$ 上一点（不与点A重合），连接 $C P$ ，将线段 $C P$ 绕点 $C$ 逆时针旋转 $60 °$ 得到线段 $C Q$ ，连接 $Q B$ ．

(1)、求证： $A P = B Q$ ；

(2)、连接 $P B$ 并延长交直线 $C Q$ 于点 $D$ ．若 $P D ⊥ C Q$ ，
①试猜想 $B C$ 和 $B Q$ 的数量关系，并证明；
②若 $A C = 2 \sqrt{2}$ ，求 $P B$ 的长.

查看试题解析
23. 如图，国家会展中心大门的截面图是由抛物线 $A D B$ 和矩形 $O A B C$ 构成.矩形 $O A B C$ 的边 $O A = \frac{3}{4}$ 米， $O C = 9$ 米，以 $O C$ 所在的直线为 $x$ 轴，以 $O A$ 所在的直线为 $y$ 轴建立平面直角坐标系，抛物线顶点 $D$ 的坐标为 $(\frac{9}{2} ， \frac{24}{5})$ .

(1)、求此抛物线对应的函数表达式；

(2)、近期需对大门进行粉刷，工人师傅搭建一木板 $O M$ ，点 $M$ 正好在抛物线上，支撑 $M N ⊥ x$ 轴， $O N = 7.5$ 米，点 $E$ 是 $O M$ 上方抛物线上一动点，且点 $E$ 的横坐标为 $m$ ，过点 $E$ 作 $x$ 轴的垂线，交 $O M$ 于点 $F$ .
①求 $E F$ 的最大值.②某工人师傅站在木板 $O M$ 上，他能刷到的最大垂直高度是 $\frac{12}{5}$ 米，求他不能刷到大门顶部的对应点的横坐标的范围.

查看试题解析