黑龙江省齐齐哈尔市讷河市2021-2022学年八年级下学期期末数学试题

试卷更新日期：2023-05-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式中，计算正确的是（）

A、 $\sqrt{2} + \sqrt{5} = \sqrt{7}$ B、 $\sqrt{{(- 5)}^{2}} = - 5$ C、（ $- \sqrt{2}$ ）²＝2 D、2 $\sqrt{3} \times 3 \sqrt{3} = 6 \sqrt{3}$

查看试题解析
2. 下列二次根式是最简二次根式的是（）

A、 $\sqrt{8}$ B、 $\sqrt{\frac{1}{2}}$ C、 $\sqrt{m^{2} + 4}$ D、 $\sqrt{27}$

查看试题解析
3. 下列各线段的长，能构成直角三角形的是 $($ $)$

A、2，3，4 B、5，12，13 C、4，6，9 D、5，11，13

查看试题解析
4. 直线 $y = 3 x + 1$ 向下平移2个单位，所得直线的解析式是（）

A、 $y = 3 x + 3$ B、 $y = 3 x - 2$ C、 $y = 3 x + 2$ D、 $y = 3 x - 1$

查看试题解析
5. 小花放学回家走了一段路，在途径的书店买了一些课后阅读书籍，然后发现时间比较晚了，急忙跑步回到家．若设小花与家的距离为s（米），她离校的时间为t（分钟），则反映该情景的大致图象为（）

A、 B、 C、 D、

查看试题解析
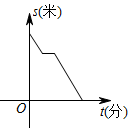6. 学校组织爱国诗词朗诵比赛，有17位同学晋级决赛，每位选手得分各不相同．小红想要确定自己是否进入前8名；除了知道自己的得分以外，她还要了解这17名同学得分的（）

A、众数 B、中位数 C、方差 D、平均数

查看试题解析
7. 如图，直线y＝- $\frac{1}{2} x + 2$ 分别交x轴于点A，y轴于点B，点D、E分别是线段AB、AO的中点，连接DE，则DE的长是（　　）

A、4 B、2 C、1 D、 $\frac{1}{2}$

查看试题解析
8. 如图，正方形ABCD中，点E是对角线BD上的一点，且 $B E = A B$ ，连接CE，AE，则 $∠ D A E$ 的度数为（）

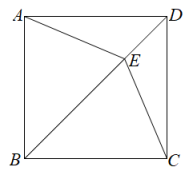A、22.5° B、25° C、30° D、32.5°

查看试题解析
9. 如图，菱形ABCD的对角线AC，BD相交于点O，过点D作DH⊥BC于点H，连接OH，若OA＝4，S_菱形ABCD＝24，则OH的长为（　　）

A、 $\sqrt{5}$ B、3 C、 $\frac{5}{2}$ D、 $\frac{12}{5}$

查看试题解析
10. 一次函数 $y_{1} = a x + b$ 与 $y_{2} = c x + d$ 的图象如图所示，下列说法：① $a b ＜ 0$ ；②函数 $y = a x + d$ 不经过第一象限；③不等式 $a x + b ＞ c x + d$ 的解集是 $x ＜ 3$ ；④ $a - c = \frac{1}{3} (d - b)$ ．其中正确的个数有（）

A、4 B、3 C、2 D、1

查看试题解析

二、填空题

11. 在函数y= $\frac{\sqrt{1 + x}}{x + 2}$ 中，自变量x的取值范围是．

查看试题解析
12. 如图，在 $▱ A B C D$ 中，对角线 $A C 、 B D$ 相交于点O，在不添加任何辅助线的情况下，请你加一个条件，使 $▱ A B C D$ 是菱形．

查看试题解析
13. 甲、乙两名同学参加“古诗词大赛”活动，五次比赛成绩的平均分都是85分，如果甲比赛成绩的方差为S_甲²=16.7，乙比赛成绩的方差为S_乙²=28.3，那么成绩比较稳定的是（填“甲”或“乙”）

查看试题解析
14. 若 $y = (m + 1) x^{| m |} + 3$ 是关于 $x$ 的一次函数，则 $m =$ ．

查看试题解析
15. 已知四边形ABCD中， $∠ A B C = 60 °$ ， $A D ∥ B C$ ， $A B = C D$ ，若 $A B = 6$ ， $B C = 9$ ，则四边形ABCD的面积为．

查看试题解析
16. 如图，正方形 $A B C D$ 和正方形 $D E F G$ 的边长分别为3和2，点E、G分别为 $A D 、 C D$ 边上的点，H为 $B F$ 的中点，连接 $H G$ ，则 $H G$ 的长为．

查看试题解析
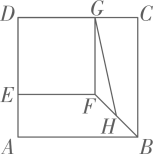17. 如图，在平面直角坐标系中，点 $A_{1} (1 ， 1)$ 在直线y＝x图象上，过 $A_{1}$ 点作y轴平行线，交直线y＝-x于点 $B_{1}$ ，以线段 $A_{1} B_{1}$ 为边在右侧作正方形 $A_{1}^{} B_{1}^{} C_{1}^{} D_{1}^{}$ ， $C_{1} D_{1}$ 所在的直线交y＝x的图象于点 $A_{2}$ ，交y＝-x的图象于点 $B_{2}$ ，再以线段 $A_{2} B_{2}$ 为边在右侧作正方形 $A_{2} B_{2} C_{2} D_{2}$ …依此类推．按照图中反映的规律，则点 $A_{2022}$ 的坐标是．

查看试题解析

三、解答题

18. 计算：

(1)、 $(\sqrt{24} + \sqrt{50}) \div \sqrt{2} - 6 \sqrt{\frac{1}{3}}$

(2)、 $202 2^{0} - | 1 - \sqrt{3} | + {(- \frac{1}{2})}^{- 2} - \sqrt{{(- 3)}^{2}}$

查看试题解析
19. 如图，在△ABC中，AD为BC边上的高，若BD＝4，DC＝5，AD＝2 $\sqrt{5}$ ，判断△ABC的形状，并说明理由．

查看试题解析
20. 如图，在平行四边形ABCD中，EF是直线DB上的两点，DE＝BF．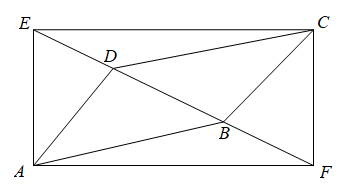

(1)、求证：四边形AFCE是平行四边形；

(2)、若四边形AFCE是矩形，且BD⊥AD，AB＝5，AD＝3，求DE的长．

查看试题解析
21. 为了解某校八年级男生的体能情况，体育老师随机抽取部分男生进行引体向上测试，并对成绩进行了统计，绘制出统计图1和图2，请根据相关信息，解答下列问题：

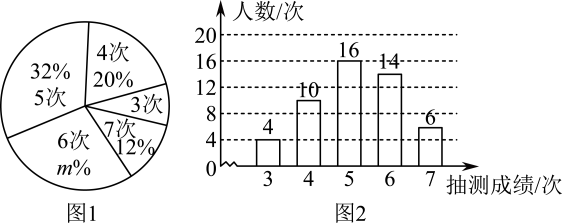(1)、本次抽测的男生人数为，图1中m的值为；

(2)、本次抽测的这组数据的平均数为次，众数为次；

(3)、若规定引体向上5次以上（含5次）为体能达标，根据样本数据，估计该校350名八年级男生中有多少人体能达标．

查看试题解析
22. 2022年4月，乙市发生疫情，各地纷纷支援．甲市政府迅速组织医护人员和抗疫物资星夜出征驰援乙市同心抗疫．如图，运输防疫物资的货车和载有医护人员的客车先后从甲市出发驶向乙市，线段OA表示货车离出发地甲市的距离y（km）与时间x（h）之间的函数关系，折线BCDE表示客车离出发地甲市的距离y（km）与时间x（h）之间的函数关系．请结合图象信息，解答下列问题：

(1)、载有医护人员的客车中途在高速服务站休息了一段时间，休息时间为h．甲、乙两市距离为km．

(2)、求线段DE对应的函数关系式．（不用求自变量的取值范围）

(3)、直接写出客车从甲市出发后经过多长时间追上货车．

查看试题解析
23. 综合与实践
折纸是同学们喜欢的手工活动之一，通过折纸我们既可以得到许多美丽的图形，同时折纸的过程还蕴含着丰富的数学知识．
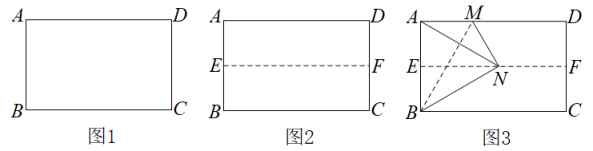
实践操作：如图1，在矩形纸片ABCD中， $A B = 4 c m$ ．
第一步：如图2，对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平．
第二步：如图3，再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM．同时，得到了线段BN．
解决问题

(1)、在图3中，EN与AB的关系是． $E N =$ cm．

(2)、在图3中，连接AN，试判断 $△ A B N$ 的形状，并给予证明．

(3)、拓展应用
已知，在矩形ABCD中， $A B = 4 c m$ ， $A D = 8 c m$ ，点P在边AD上，将 $△ A B P$ 沿着BP折叠，若点A的对应点 $A^{'}$ 恰落在矩形ABCD的对称轴上，则 $A P =$ cm．

查看试题解析
24. 综合与探究
如图，直线 $l_{1} ： y = k x + b$ 与x轴、y轴分别交于A、B两点，且 $O B = 4$ ， $A B = 5$ ，点D（t，0）
是x轴上一点，过D点作直线 $l_{2} ⊥ x$ 轴．

(1)、求直线 $l_{1}$ 的解析式；

(2)、当 $t = 1$ 时，点P在直线 $l_{2}$ 上，当 $P A + P B$ 的值最小时，求点P坐标；

(3)、当 $t =$ 时， $△ A B D$ 的面积为4；

(4)、当 $t = 2$ 时，在坐标平面内是否存在点Q，使以点A、B、D、Q为顶点的四边形是平行四边形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．

查看试题解析