黑龙江省牡丹江市林口县2021-2022学年八年级下学期期末考试数学试题

试卷更新日期：2023-05-05 类型：期末考试

进入出卷网下载

一、填空题

1. 若二次根式 $\sqrt{- x + 2}$ 实数范围内有意义，则x的取值范围是．

查看试题解析
2. 如图，菱形 $A B C D$ 的一边中点M到对角线交点O的距离为 $1.5 c m$ ，则菱形 $A B C D$ 周长为．

查看试题解析
3. 已知 $P_{1}$ （-1， $y_{1}$ ）， $P_{2}$ （4， $y_{2}$ ）是一次函数y＝x＋1图象上的两个点，则 $y_{1}$ $y_{2}$ （填“＞”、“＜”或“＝”）．

查看试题解析
4. 如图， $▱$ ABCD中，点E在边 $B C$ 上，以 $A E$ 为折痕，将 $△ A B E$ 向上翻折，点B正好落在 $C D$ 上的点F处，若 $△ F C E$ 的周长为 $7$ ， $△ F D A$ 的周长为 $21$ ，则 $▱$ ABCD的周长是．

查看试题解析
5. 如图，三级台阶，每一级的长、宽、高分别为8dm、3dm、 $2 d m$ ，A和B是这个台阶上两个相对的端点，点A处有一只蚂蚁，想到点B处去吃可口的食物，则蚂蚁沿着台阶面爬行到点B的最短路程为dm．

查看试题解析
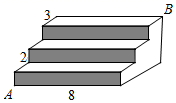6. 若直线 $y = k x + 2$ 与两条坐标轴围成的三角形的面积是1，则k的值为．

查看试题解析
7. 如图，△ABC中，∠B＝90°，AB＝3，BC＝4，CD＝12，AD＝13，点E是AD的中点，则CE的长为．

查看试题解析
8. 2022年4月21日中国航天日，某校举办了以“航天点亮梦想”为主题的中学生知识竞赛中，五位评委分别给甲队、乙队两组选手的评分如下：
甲队：8，7，9，8，8；乙队：7，9，6，9，9．
则下列说法：①从甲、乙得分的平均分看，他们两人的成绩没有差别；
②从甲、乙得分的众数看，乙的成绩比甲好；
③从甲、乙得分的中位数看，甲的成绩比乙好；
④从甲、乙成绩的稳定性看，甲的成绩比乙好；正确的是．

查看试题解析

二、单选题

9. 下列图形中，既是中心对称图形又是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
10. 实数 $\sqrt{7}$ 的倒数是（）

A、 $- \sqrt{7}$ B、 $\pm \sqrt{7}$ C、 $\frac{\sqrt{7}}{7}$ D、 $\frac{1}{7}$

查看试题解析
11. 满足下列条件的△ABC不是直角三角形的是（）

A、∠A∶∠B∶∠C＝1∶1∶2 B、BC∶AC∶AB＝5∶12∶14 C、BC＝1，AC＝2，AB＝ $\sqrt{5}$ D、BC＝3，AC＝4，AB＝5

查看试题解析
12. 在 $▱ A B C D$ 中， $∠ B ＋ ∠ D ＝ 240 °$ ，那么∠A的度数是（）

A、60° B、80° C、100° D、120°

查看试题解析
13. 在“传唱红色经典，弘扬爱国精神”比赛中，七位评委给某选手打出了7个原始分，如果规定：去掉一个最高分和一个最低分，余下5个有效分的平均值作为这位选手的最后得分，则7个原始分和5个有效分这两组数据相比较，一定不会发生改变的是（）

A、方差 B、加权平均数 C、平均数 D、中位数

查看试题解析
14. 下列计算正确的是（）

A、 $\sqrt{{(- 3)}^{2}} = - 3$ B、 $3 \sqrt{2} - \sqrt{2} = 3$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $\sqrt{10} \div \sqrt{5} = 2$

查看试题解析
15. 如图，直线y=-x+1与x轴交于点A，与y轴交于点B，以点A为圆心， $A B$ 为半径画弧，交x轴于点C，则点C坐标为（）

A、 $(1 - \sqrt{2} ， 0)$ B、 $(\sqrt{2} - 1 ， 0)$ C、 $(- \sqrt{2} ， 0)$ D、 $(- 1 ， 0)$

查看试题解析
16. 如图，矩形 $A B C D$ 的对角线 $A C$ ， $B D$ 相交于点O， $∠ A C D = 30 °$ ，若 $A O = 5$ ，则 $A B$ 的长为（）．

A、 $10 \sqrt{3}$ B、 $5 \sqrt{3}$ C、10 D、20

查看试题解析
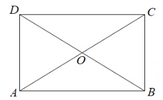17. 将直线 $y = \frac{1}{2} x$ 向上平移2个单位长度后得到直线y＝kx＋b，则下列关于直线y＝kx＋b的说法正确的是（）

A、直线经过一、三、四象限 B、y随x的增大而减小 C、与y轴交于（2，0） D、与x轴交于（－4，0）

查看试题解析
18. A、B两地相距 $350 k m$ ，甲骑摩托车从A地匀速驶向B地．当甲行驶 $1$ 小时途径C地时，一辆货车刚好从C地出发匀速驶向B地，当货车到达B地后立即掉头以原速匀速驶向A地．如图表示两车与B地的距离 $y (k m)$ 和甲出发的时间 $x (h)$ 的函数关系．则下列说法错误的是（）

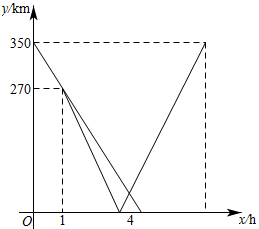A、甲行驶的速度为 $80 k m / h$ B、货车返回途中与甲相遇后又经过 $\frac{3}{8} h$ 甲到B地 C、甲行驶 $2.7$ 小时时货车到达B地 D、甲行驶到B地需要 $\frac{35}{8} h$

查看试题解析
19. 如图，在平面直角坐标系中，O是菱形ABCD对角线BD的中点，AD $∥$ x轴，AD＝2，∠A＝60°．将菱形ABCD绕点O旋转，使点D落在y轴上，则旋转后点A的对应点的坐标是（）．

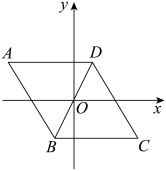A、 $(\sqrt{3} ， 0)$ 或 $(- \sqrt{3} ， 0)$ B、 $(\sqrt{3} ， 0)$ C、 $(- \sqrt{3} ， 0)$ D、 $(0 ， \sqrt{3})$ 或 $(0 ， - \sqrt{3})$

查看试题解析
20. 如图，在正方形ABCD中，对角线AC、BD交于点O， $∠ B C E = \frac{1}{2} ∠ A C B$ ， CE交BO于点E，过点B作 $B F ⊥ C E$ ，垂足为F，交AC于点G．现给出下列结论：① $B C = C G$ ；② $△ A B G ≌ △ B C E$ ；③BE＋GC＝BD；④若OC＝ $\sqrt{2}$ ，则 $S_{Δ B C G} = \sqrt{2}$ ．其中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

三、解答题

21. 计算：

(1)、 $(3 \sqrt{48} - 2 \sqrt{27}) \div \sqrt{6}$

(2)、 ${(3 + \sqrt{2})}^{2} - \sqrt{8} \times (3 - 3 \sqrt{2})$

查看试题解析
22. 矩形ABCD的对角线AC，BD相交于点O，AC＝ $2 \sqrt{5}$ ， BC＝2，向矩形ABCD外作 $Δ C D E$ ，使 $Δ C D E$ 为等腰直角三角形，且点E不在边BC所在的直线上，请画出图形，直接写出OE的长．

查看试题解析
23. 某校拟派一名跳高运动员参加校际比赛，对甲、乙两名同学进行了8次跳高选拔比赛，他们的原始成绩（单位：cm）如下表：
学生/成绩/次数
第1次
第2次
第3次
第4次
第5次
第6次
第7次
第8次
甲
169
165
168
169
172
173
169
167
乙
161
174
172
162
163
172
172
176
两名同学的8次跳高成绩数据分析如下表：
学生/成绩/名称
平均数（单位：cm）
中位数（单位：cm）
众数（单位：cm）
方差（单位：cm²）
甲
a
169
c
5.75
乙
169
b
172
31.25
根据图表信息回答下列问题：

(1)、a＝， b＝， c＝；

(2)、这两名同学中，的成绩更为稳定；（填甲或乙）

(3)、若预测跳高165就可能获得冠军，该校为了获取跳高比赛冠军，你认为应该选择同学参赛，理由是：；

(4)、若预测跳高170方可夺得冠军，该校为了获取跳高比赛冠军，你认为应该选择同学参赛，班由是：．

查看试题解析
24. 已知，在△ABC中，∠BAC=90°，∠ABC=45°，D为直线BC上一动点（不与点B，C重合），以AD为边作正方形ADEF，连接CF．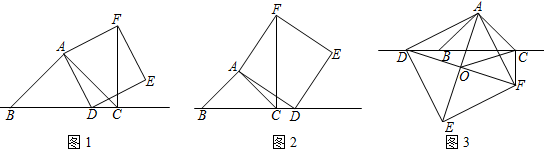

(1)、如图1，当点D在线段BC上时，BC与CF的位置关系是， BC、CF、CD三条线段之间的数量关系为；

(2)、如图2，当点D在线段BC的延长线上时，其他条件不变，请猜想BC与CF的位置关系BC，CD，CF三条线段之间的数量关系并证明；

(3)、如图3，当点D在线段BC的反向延长线上时，点A，F分别在直线BC的两侧，其他条件不变．若正方形ADEF的对角线AE，DF相交于点O，OC= $\frac{13}{2}$ ， DB=5，则△ABC的面积为．（直接写出答案）

查看试题解析
25. 端午节前夕，某商铺用620元购进50个肉粽和30个蜜枣粽，肉粽的进货单价比蜜枣粽的进货单价多6元．

(1)、肉粽和蜜枣粽的进货单价分别是多少元？

(2)、由于粽子畅销，商铺决定再购进这两种粽子共300个，其中肉粽数量不多于蜜枣粽数量的2倍，且每种粽子的进货单价保持不变，若肉粽的销售单价为14元，蜜枣粽的销售单价为6元，试问第二批购进肉粽多少个时，全部售完后，第二批粽子获得利润最大？第二批粽子的最大利润是多少元？

查看试题解析
26. 如图，在平面直角坐标系中，直线y＝ $\frac{5}{2}$ x+5与x轴交于点A，与y轴交于点B，过点B的另一直线交x轴正半轴于C，且△ABC面积为15.

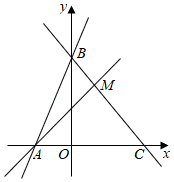(1)、求点C的坐标及直线BC的表达式；

(2)、若M为线段BC上一点，且△ABM的面积等于△AOB的面积，求M的坐标；

(3)、在（2）的条件下，点E为直线AM上一动点，在x轴上是否存在点D，使以点D、E、B、C为顶点的四边形为平行四边形？若存在，直接写出点D的坐标；若不存在，请说明理由.

查看试题解析

学生/成绩/次数	第1次	第2次	第3次	第4次	第5次	第6次	第7次	第8次
甲	169	165	168	169	172	173	169	167
乙	161	174	172	162	163	172	172	176

学生/成绩/名称	平均数（单位：cm）	中位数（单位：cm）	众数（单位：cm）	方差（单位：cm²）
甲	a	169	c	5.75
乙	169	b	172	31.25