黑龙江省鹤岗市萝北县2021-2022学年下学期八年级期末数学试卷（五四学制）

试卷更新日期：2023-05-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，可与 $\sqrt{12}$ 进行合并的二次根式为（）

A、 $\sqrt{6}$ B、 $\sqrt{32}$ C、 $\sqrt{18}$ D、 $\sqrt{75}$

查看试题解析
2. 下列命题中，错误的是（）．

A、平行四边形的对角线互相平分 B、菱形的对角线互相垂直平分 C、矩形的对角线相等且互相垂直平分 D、角平分线上的点到角两边的距离相等

查看试题解析
3. 如图， $E F$ 过 $▱ A B C D$ 对角线的交点O，交 $A D$ 于E，交 $B C$ 于F，若 $▱ A B C D$ 的周长为36， $O E = 3$ ，则四边形 $A B F E$ 的周长为（）

A、24 B、26 C、28 D、20

查看试题解析
4. 若式子 $\sqrt{k - 1} + (k - 1)^{0}$ 有意义，则一次函数 $y = (k - 1) x + k - 1$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
5. 如图，在菱形 $A B C D$ 中， $∠ A = 6 0^{∘}$ ， $A D = 8$ ． $P$ 是 $A B$ 边上的一点， $E$ ， $F$ 分别是 $D P$ ， $B P$ 的中点，则线段 $E F$ 的长为（）

A、8 B、 $2 \sqrt{5}$ C、4 D、 $2 \sqrt{2}$

查看试题解析
6. 若 $x + y = 3 + 2 \sqrt{2}$ ， $x - y = 3 - 2 \sqrt{2}$ ，则 $\sqrt{x^{2} - y^{2}}$ 的值为（）

A、 $4 \sqrt{2}$ B、 $1$ C、 $6$ D、 $3 - 2 \sqrt{2}$

查看试题解析
7. 如图，平行四边形ABCD的对角线AC与BD相交于点O ， AE⊥BC于E ， AB＝ $\sqrt{3}$ ，AC＝2，BD＝4，则AE的长为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{3}{2}$ C、 $\frac{\sqrt{21}}{7}$ D、 $\frac{2 \sqrt{21}}{7}$

查看试题解析
8. 一次“我的青春，我的梦”演讲比赛，有五名同学的成绩如表所示，有两个数据被遮盖，那么被遮盖的两个数据依次是（　　）
组员及项目
甲
乙
丙
丁
戊
方差
平均成绩
得分
$81$
$79$
$■$
$80$
$82$
$■$
$80$

A、 $80$ ， $2$ B、 $80$ ， $\sqrt{2}$ C、 $78$ ， $2$ D、 $78$ ， $\sqrt{2}$

查看试题解析
9. 学校离小林家距离为2千米，某天他放学后骑自行车回家，行驶了5分钟后，因故停留10分钟，然后又行驶了5分钟到家，在下列图形中能大致描述他回家过程中离家的距离s（千米）与所用时间t（分）之间的函数关系是（）

A、 B、 C、 D、

查看试题解析
10. 如图，点 $E$ 在正方形 $A B C D$ 的对角线 $A C$ 上，且 $E C = 2 A E$ ， $Rt Δ F E G$ 的两直角边 $E F$ ， $E G$ 分别交 $B C$ ， $D C$ 于点 $M$ ， $N$ .若正方形 $A B C D$ 的边长为 $a$ ，则重叠部分四边形 $E M C N$ 的面积为（）

A、 $\frac{2}{3} a^{2}$ B、 $\frac{1}{4} a^{2}$ C、 $\frac{5}{9} a^{2}$ D、 $\frac{4}{9} a^{2}$

查看试题解析

二、填空题

11. 要使式子 $\frac{\sqrt{x + 3}}{x - 1}$ 有意义,则x的取值范围为．

查看试题解析
12. 已知把一次函数 $y = 2 x + 3$ 的图象向右平移3个单位长度，则平移后图象的函数解析式为．

查看试题解析
13. 如图，在四边形ABCD中，对角线AC，BD交于点O，OA=OC，OB=OD，添加一个条件使四边形ABCD是菱形，那么所添加的条件可以是（写出一个即可）．

查看试题解析
14. 直线l₁：y＝x+1与直线l₂：y＝mx+n相交于点P（a，2），则关于x的不等式x+1≥mx+n的解集为．

查看试题解析
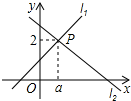15. 已知在△ABC中，AB=13cm，AC=15cm，高AD=12cm．则△ABC的周长为．

查看试题解析
16. 在实数范围内分解因式4m²－7= ．

查看试题解析
17. 某招聘考试分笔试和面试两种，其中笔试按60%、面试按40%计算加权平均数，作为总成绩．孔明笔试成绩90分，面试成绩85分，那么孔明的总成绩是　分．

查看试题解析
18. 如图，正方形ABCD的边长为9，将正方形折叠，使D点落在BC边上的点E处，折痕为GH．若BE：EC=2：1，则线段CH的长是．

查看试题解析
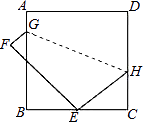19. 已知两点M（3，5），N（1，1），点P是x轴上一动点，若使PM+PN最短，则点P的坐标应为．

查看试题解析
20. 如图，矩形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点O， $A E$ 平分 $∠ B A D$ 交 $B C$ 于点E，连接 $O E$ ，若 $O E ⊥ B C$ ， $O E = 1$ ，则 $A C$ 的长为．

查看试题解析

三、解答题

21. 计算题：

(1)、 $(3 + \sqrt{5}) (3 - \sqrt{5}) - (\sqrt{3} - 1)^{2}$ ；

(2)、 $(2 \sqrt{48} - 3 \sqrt{27}) \div \sqrt{6}$ ．

查看试题解析
22. 先化简，再求值．
$(\frac{a}{a - b} - 1) \div \frac{b}{a^{2} - b^{2}}$ ，其中a= $\sqrt{3}$ +1，b= $\sqrt{3}$ -1．

查看试题解析
23. 已知y与 $x + 2$ 成正比例，且当 $x = 1$ 时， $y = - 6$ ．

(1)、求y与x之间的函数解析式；

(2)、若点 $P (n ， 4)$ 在这个函数的图象上，求n的值．

查看试题解析
24. 如图是某中学男田径队队员年龄结构条形统计图，根据图中信息解答下列问题：

(1)、田径队共有多少人？

(2)、该队队员年龄的众数和中位数分别是多少？

(3)、该队队员的平均年龄是多少？

查看试题解析
25.
昨天早晨7点，小明乘车从家出发，去西安参加中学生科技创新大赛，赛后，他当天按原路返回，如图，是小明昨天出行的过程中，他距西安的距离y（千米）与他离家的时间x（时）之间的函数图象．
根据下面图象，回答下列问题：

(1)、求线段AB所表示的函数关系式；

(2)、已知昨天下午3点时，小明距西安112千米，求他何时到家？

查看试题解析
26. 已知 $A C$ 是菱形 $A B C D$ 的对角线， $∠ B A C = 60 °$ ，点E是直线 $B C$ 上的一个动点，连接 $A E$ ，以 $A E$ 为边作菱形 $A E F G$ ，并且使 $∠ E A G = 60 °$ ，连接 $C G$ ，当点E在线段 $B C$ 上时，如图 $1$ ，易证： $A B = C G + C E$ ．

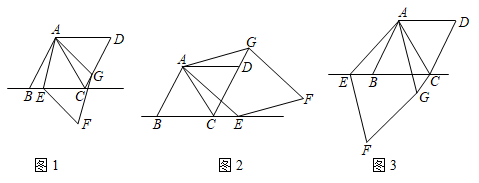(1)、当点E在线段 $B C$ 的延长线上时（如图 $2$ ），猜想 $A B$ ， $C G$ ， $C E$ 之间的关系并证明；

(2)、当点E在线段 $C B$ 的延长线上时（如图 $3$ ），直接写出 $A B$ ， $C G$ ， $C E$ 之间的关系．

查看试题解析
27. 为保障我国海外维和部队官兵的生活，现需通过A港口、B港口分别运送100吨和50吨生活物资．已知该物资在甲仓库存有80吨，乙仓库存有70吨，若从甲、乙两仓库运送物资到港口的费用（元/吨）如表所示：
港口
运费（元/吨）
甲库
乙库
A港
14
20
B港
10
8

(1)、设从甲仓库运送到A港口的物资为x吨，求总运费y（元）与x（吨）之间的函数关系式，并写出x的取值范围；

(2)、求出最低费用，并说明费用最低时的调配方案．

查看试题解析
28. 在平面直角坐标系 $x O y$ 中，直线 $y = k x + 4 (k \neq 0)$ 与y轴交于点A．

(1)、如图，直线 $y = - 2 x + 1$ 与直线 $y = k x + 4 (k \neq 0)$ 交于点B，与y轴交于点C，点B的横坐标为 $- 1$ ．
①求点B的坐标及k的值；
②直线 $y = - 2 x + 1$ 、直线 $y = k x + 4$ 与y轴所围成的 $△ A B C$ 的面积等于多少？

(2)、在（1）的条件下直线 $y = k x + 4 (k \neq 0)$ 与x轴交于点E，在x轴上是否存在点F，使 $△ A E F$ 是以 $A E$ 为腰的等腰三角形？如存在，请直接写出点F的坐标．

查看试题解析

组员及项目	甲	乙	丙	丁	戊	方差	平均成绩
得分	$81$	$79$	$■$	$80$	$82$	$■$	$80$

港口	运费（元/吨）
港口	甲库	乙库
A港	14	20
B港	10	8