黑龙江省哈尔滨市双城区2021-2022学年八年级下学期期末考试数学试题

试卷更新日期：2023-05-05 类型：期末考试

进入出卷网下载

一、单选题

1. 若 $\sqrt{m}$ 是二次根式，则m的值可能是（）

A、-3 B、-2 C、-1 D、2

查看试题解析
2. 下列各组数中，能构成直角三角形的是（）

A、1， $\sqrt{2}$ ， $\sqrt{3}$ B、4，5，6 C、2，3，4 D、2， $\sqrt{2}$ ， 3

查看试题解析
3. 一组数据5，3， 3，6， 9，4，3，5，12的中位数是（）

A、3 B、4 C、5 D、6

查看试题解析
4. 一次函数y＝kx－1的图象经过点 $(2 ， - 3)$ ，则k＝（）

A、1 B、－1 C、2 D、－2

查看试题解析
5. 矩形具有而平行四边形不一定具有的性质是（）

A、对边相等 B、对角相等 C、对角线相等 D、对角线互相平分

查看试题解析
6. 如图，菱形ABCD的对角线AC、BD的长分别为6和8，则这个菱形的周长是（）。

A、20 B、24 C、40 D、48

查看试题解析
7. 如图，在 $△ A B C$ 中， $A B = 4$ ， $A C = 5$ ， $B C = 6$ ，点D，E，F分别是AB，BC，CA的中点，连结DE，EF，则四边形ADEF的周长为（）

A、6 B、9 C、12 D、15

查看试题解析
8. 一条直线y=kx+b，其中k+b=﹣5、kb=6，那么该直线经过（）

A、第二、四象限 B、第一、二、三象限 C、第一、三象限 D、第二、三、四象限

查看试题解析
9. 如图，在 $R t Δ A B C$ 中， $∠ B = 90 °$ ， $A B = 3$ ， $B C = 4$ ，将 $Δ A B C$ 折叠，使点B恰好落在边 $A C$ 上，与点 $B^{'}$ 重合， $A E$ 为折痕，则 $E C$ 长为（）

A、3 B、1.5 C、2.5 D、1

查看试题解析
10. 甲、乙两名选手参加长跑比赛，他们的行程y（km）随时间x（h）变化的图象（全程）如图所示，有下列说法：
①在起跑后1h内，甲在乙的前面；
②甲在第1.5h时的行程为12km；
③乙比甲早0.3h到达终点；
④本次长跑比赛的全程为20km．
其中正确说法的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 计算 $\sqrt{8} - 3 \sqrt{\frac{1}{2}}$ 的结果是．

查看试题解析
12. 使 $\sqrt{3 x - 1}$ 有意义的x的取值范围是．

查看试题解析
13. 将直线 $y ＝ 3 x + 2$ 向上平移m个单位长度得到新直线 $y ＝ 3 x + 6$ ，则m的值为．

查看试题解析
14. 已知一组数据x₁ ， x₂ ， x₃ ， x₄ ， x₅的方差是 $\frac{1}{4}$ ，那么另一组数据2x₁－2，2x₂－2，2x₃－2，2x₄－2，2x₅－2的方差是．

查看试题解析
15. 已知2＜a＜3，化简： $\sqrt{a^{2} - 2 a + 1} + \sqrt{(a - 4)^{2}} =$ ．

查看试题解析
16. 若不等式组 ${\begin{array}{l} x < a \\ x + 2 > 2 a \end{array}$ 无解，则a的取值范围是.

查看试题解析
17. 如图，在 $△ A B C$ 中， $A B = A C = 8$ ， $∠ B A C = 120^{°}$ ，AD是 $△ A B C$ 的中线，AE是 $∠ B A D$ 的角平分线， $D F ∥ A B$ 交AE的延长线于点F，则DF的长为.

查看试题解析
18. 已知平行四边形ABCD，对角线AC垂直于平行四边形一边AB，AB＝1，平行四边形ABCD的面积为 $\sqrt{3}$ ， P为直线BC上一点，若点P到直线AC的距离为 $\frac{1}{4}$ ，则PB的长为．

查看试题解析
19. 当直线 $y = (2 - 2 k) x + k - 3$ 经过第二、三、四象限时，则 $k$ 的取值范围是．

查看试题解析
20. 如图，在矩形ABCD中，AB＝5，AD＝3，动点P满足3S_△PAB＝S_矩形ABCD，则点P到A、B两点距离之和PA＋PB的最小值为.

查看试题解析

三、解答题

21. 先化简，再求值： $(\frac{2}{x + 3} + \frac{4}{x^{2} - 9}) \div \frac{x - 1}{x + 3}$ ， $其中 x ＝ \sqrt{2} ＋ 3$

查看试题解析
22. 如图，在平面直角坐标系中，已知 $Δ A B C$ 的三个顶点的坐标分别为 $A (1 ， 2)$ ， $B (5 ， 1)$ ， $C (3 ， - 2)$ ．

（1）将 $Δ A B C$ 先向上平移3个单位长度，再向左平移6个单位长度，得到 $Δ A_{1} B_{1} C_{1}$ ，画出 $Δ A_{1} B_{1} C_{1}$ ，并写出A的对应点 $A_{1}$ 的坐标；
（2）将 $Δ A B C$ 绕原点O顺时针方向旋转 $90 °$ 得到 $Δ A_{2} B_{2} C_{2}$ ，请在直角坐标系中画出 $Δ A_{2} B_{2} C_{2}$ ，并写出B的对应点 $B_{2}$ 的坐标．

查看试题解析
23. 某校八年级全体同学参加了某项捐款活动，随机抽查了部分同学捐款的情况，并统计绘制成了如图两幅不完整的条形统计图和扇形统计图，请根据所提供的信息，解答下列问题：

(1)、本次共抽查学生人，并将条形图补充完整；

(2)、捐款金额的众数是，中位数是；

(3)、在八年级850名学生中，捐款20元及以上（含20元）的学生估计有多少人？

查看试题解析
24. 如图，在平行四边形 $A B C D$ 中， $∠ A C B ＝ 90 °$ ，过点 D 作 $D E ⊥ B C$ 交 $B C$ 的延长线于点 E．

(1)、求证：四边形 $A C E D$ 是矩形；

(2)、连接 $A E$ 交 $C D$ 于点 F，连接 $B F$ ．若 $∠ A B C ＝ 60 °$ ， $C E ＝ 2$ ，求 $B F$ 的长．

查看试题解析
25. 为提升青少年的身体素质,深圳市在全市中小学推行“阳光体育”活动,某学校为满足学生的需求,准备再购买一些篮球和足球.已知用800元购买篮球的个数比购买足球的个数少2个,足球的单价为篮球单价的 $\frac{4}{5}$ .

(1)、求篮球、足球的单价分别为多少元?

(2)、如果计划用不多于5200元购买篮球、足球共60个 ,那么至少要购买多少个足球?

查看试题解析
26. 已知四边形ABCD是菱形，点F在CD上，点E在BC的延长线上，连接AE、BF交于点H，∠AHB＝∠ADC．

(1)、如图1，当点F与点D重合时，求证：AE＝BF

(2)、如图2，当点F不与点D重合时，（1）中结论是否成立？如果成立，请证明；如果不成立，请说明理由．

(3)、在（2）的条件下，若AB＝13，CF＝11，BF＝20，求CE的长

查看试题解析
27. 如图1，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为（﹣3，4），点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H，连接BM.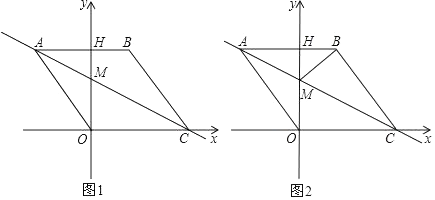

(1)、菱形ABCO的边长

(2)、求直线AC的解析式；

(3)、动点P从点A出发，沿折线ABC方向以2个单位/秒的速度向终点C匀速运动，设△PMB的面积为S（S≠0），点P的运动时间为t秒，
①当0＜t＜ $\frac{5}{2}$ 时，求S与t之间的函数关系式；
②在点P运动过程中，当S=3，请直接写出t的值．

查看试题解析