黑龙江省哈尔滨市南岗区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2023-05-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各组数据中，不能构成直角三角形的一组数是（）

A、1.5，2，3 B、5，12，13 C、 $\frac{5}{4}$ ， 1， $\frac{3}{4}$ D、3，4，5

查看试题解析
2. 已知 $▱$ ABCD中．AB＝5，BC＝3．则 $▱$ ABCD的周长为（）

A、20 B、16 C、12 D、10

查看试题解析
3. 在平面直角坐标系中，一次函数y＝2x－3的图象经过（）

A、第一、二、三象限 B、第一、三、四象限 C、第一、二、四象限 D、第二、三、四象限

查看试题解析
4. 如图，在△ABC中，∠C＝90°，AD是△ABC的角平分线，DE⊥AB于点E，若CD＝3，BD＝5，则线段BE的长为（）

A、2 B、3 C、4 D、5

查看试题解析
5. 已知正比例函数y=（k+5）x，且y随x的增大而减小，则k的取值范围是（）

A、k>5 B、k<5 C、k>−5 D、k<−5

查看试题解析
6. 某市2018年底森林覆盖率为63%．为贯彻落实“绿水青山就是金山银山”的发展理念，该市大力开展植树造林活动，2020年底森林覆盖率达到68%，如果这两年森林覆盖率的年平均增长率为x，那么，正确的方程是（）

A、 $0.63 (1 + x) = 0.68$ B、 $0.63 {(1 + x)}^{2} = 0.68$ C、 $0.63 (1 + 2 x) = 0.68$ D、 $0.63 {(1 + 2 x)}^{2} = 0.68$

查看试题解析
7. 如图，在△ABC中，∠ACB＝90°．若AB＝15，则正方形ADEC和正方形BCFG的面积和为（）

A、150 B、200 C、225 D、450

查看试题解析
8. 如图所示的木制活动衣帽架是由三个全等的菱形构成，根据实际需要可以调节 $A E$ 间的距离，若 $A E$ 间的距离调节到60 $c m$ ，菱形的边长 $A B = 20 c m$ ，则 $∠ D A B$ 的度数是（）

A、 $90 °$ B、 $100 °$ C、 $120 °$ D、 $150 °$

查看试题解析
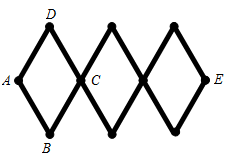9. 已知 $x = 1$ 是一元二次方程 $(m - 2) x^{2} + 4 x - m^{2} = 0$ 的一个根，则m的值为（）

A、-1或2 B、-1 C、2 D、0

查看试题解析
10. －个容器有进水管和出水管，每分钟的进水量和出水量是两个常数．从某时刻开始4min内只进水不出水，从第4min到第24min内既进水又出水，从第24min开始只出水不进水，容器内水量y（单位：L）与时间x（单位：min）之间的关系如图所示，则图中a的值是（）

A、30 B、32 C、34 D、36

查看试题解析

二、填空题

11. 函数 $y = a x + b$ 的图象如图，则方程 $a x + b = 0$ 的解为.

查看试题解析
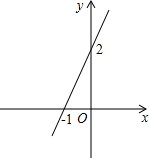12. 若平行四边形中两个内角的度数比为1：2，则其中一个较小的内角的度数是°．

查看试题解析
13. 命题“全等三角形的对应角相等”的逆命题是命题（填“真”或“假”）.

查看试题解析
14.
如图，点D、E、F分别是△ABC各边的中点，连接DE、EF、DF ．若△ABC的周长为10，则△DEF的周长为．

查看试题解析
15. 某种植物的主干长出若干数目的支干又长出同样数目的小分支，主干、支干和小分支的总数是91．设每个支干长出x个小分支，则可得方程为．

查看试题解析
16. 若y与x成正比例，当x＝5时，y＝6，则y与x的函数解析式为．

查看试题解析
17. 矩形对角线组成的对顶角中，有一组是两个50°的角．则对角线与各边组成的角是度．

查看试题解析
18. 某品牌鞋子的长度ycm与鞋子的“码”数x之间满足一次函数关系．若22码鞋子的长度为16cm，44码鞋子的长度为27cm，则38码鞋子的长度为cm．

查看试题解析
19. 对于任意实数a、b，定义一种运算： $a \otimes b = a^{2} + b^{2} - a b$ ，若 $x \otimes (x - 1) = 3$ ，则x的值为.

查看试题解析
20. 如图，在矩形ABCD中，AB＝5，点E在AD上，且 $A E = \frac{1}{4} A D$ ，点F是CD的中点，连接EF，若 $E F = \frac{13}{2}$ ，则线段AE的长为．

查看试题解析

三、解答题

21. 解方程：x（x-4）＝2-8x．

查看试题解析
22. 如图，一架2.5m长的梯子AB斜靠在一竖直的墙AO上，这时AO为2m．如果梯子的顶端A沿墙下滑0.5m（AC＝0.5m），求梯子底端B外移的距离（BD的长）．

查看试题解析
23. “黄金Ⅰ号”玉米种子的价格为5元/kg．如果一次购买2kg以上的种子，超过2kg部分的种子价格打8折．当购买量为xkg时，付款金额为y元．

(1)、求y与x的函数解析式；

(2)、利用（1）中所求的函数解析式，求一次购买3kg种子的付款金额比一次购买1.5kg种子的付款金额多多少元．

查看试题解析
24. 如图，点C是 $B E$ 的中点，四边形 $A B C D$ 是平行四边形.

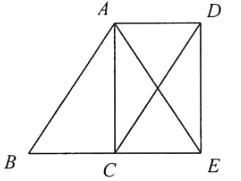(1)、求证：四边形 $A C E D$ 是平行四边形；

(2)、如果 $A B = A E$ ，求证：四边形 $A C E D$ 是矩形.

查看试题解析
25. 直播购物逐渐走进了人们的生活．某电商在抖音上对一款成本价为40元的小商品进行直播销售，如果按每件60元销售，每天可卖出20件．通过市场调查发现，每件小商品售价每降低5元，日销售量增加10件．

(1)、若日利润保持不变，商家想尽快销售完该款商品，每件售价应定为多少元？

(2)、小明的线下实体商店也销售同款小商品，标价为每件62.5元．为提高市场竞争力，促进线下销售，小明决定对该商品实行打折销售，使其销售价格不超过（1）中的售价，则该商品至少需打几折销售？

查看试题解析
26. 问题解决：
如图1，在正方形ABCD中，点E，F分别在AB，AD上，连接CE，CF，EF，且∠ECF＝45°．

(1)、求证：BE＋DF＝EF；

(2)、若AB＝6，EF＝5．AE>AF，求线段AE的长．

(3)、类比迁移：
如图2，在四边形ABCD中，∠BAD＝60°，∠BCD＝120°，对角线AC平分∠BAD，点E，F分别在AB，AD上，且AE>AF，连接CE，CF、EF，∠ECF＝60°，若 $A C = \frac{20 \sqrt{3}}{3}$ ， EF＝7，求线段AE的长．

查看试题解析
27. 如图，在平面直角坐标系中，点O为坐标系的原点，直线y＝2x＋4分别交x轴，y轴于点B，A，点C在x轴的正半轴上，连接AC，若 $S_{△ A B C} = 12$ ．

(1)、求点C的坐标；

(2)、点D在第一象限直线 $y = - x + \frac{11}{2}$ 上，连接OD，CD，设点D的横坐标为t，△OCD的面积为S，求S与t的函数解析式（不要求写出自变量t的取值范围）；

(3)、在（2）的条件下，连接AD，过点C作CE∥AD，交直线AB于点E，连接EO．若∠BEO＝∠CEO，求S的值．

查看试题解析