黑龙江省哈尔滨市道外区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2023-05-05 类型:期末考试
一、单选题
-
1. 下列方程中,是关于x的一元二次方程的是( )A、 B、 C、 D、2. 在一个直角三角形中,如果斜边长是13,一条直角边长是5,那么另一条直角边长是( ).A、6 B、8 C、10 D、123. 下列函数中,表示y是x的正比例函数的是( ).A、 B、 C、 D、4. 在平行四边形中,如果 , 那么( ).A、 B、 C、 D、5. 将方程化成一元二次方程的一般形式,正确的是( ).A、 B、 C、 D、6. 下列图形不是轴对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 7. 下列四组条件中,不能判定四边形ABCD是平行四边形的是( ).A、AB=DC,AD=BC B、 C、 , AB=DC D、 , AD=BC8. 已知正比例函数的函数值y随x的增大而增大,则m的取值范围是( )A、 B、 C、 D、9. 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示.如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么的值为( )
7. 下列四组条件中,不能判定四边形ABCD是平行四边形的是( ).A、AB=DC,AD=BC B、 C、 , AB=DC D、 , AD=BC8. 已知正比例函数的函数值y随x的增大而增大,则m的取值范围是( )A、 B、 C、 D、9. 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,如图所示.如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么的值为( ) A、12 B、13 C、25 D、16910. 某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中错误的是( ).
A、12 B、13 C、25 D、16910. 某星期六上午,小明从家出发跑步去公园,在公园停留了一会儿打车回家.图中折线表示小明离开家的路程y(米)和所用时间x(分)之间的函数关系,则下列说法中错误的是( ). A、小明跑步的速度为180米/分 B、小明在公园休息了5分钟 C、小明乘出租车用了17分钟 D、出租车的平均速度是900米/分
A、小明跑步的速度为180米/分 B、小明在公园休息了5分钟 C、小明乘出租车用了17分钟 D、出租车的平均速度是900米/分二、填空题
-
11. 函数 的自变量x的取值范围是 .12. 在菱形中, , 则对角线的长为 .13. 在平面直角坐标系中有两点和点 , 则这两点之间的距离是 .14. 若关于x的方程有两个相等的实数根,则c的值为 .15. 已知一次函数的图像经过点 , 则m= .16. 如图,平行四边形中, , 垂足分别为E、F, , 则 .
 17. 青山村种植水稻2019年平均每公顷产 , 2021年平均每公顷产 , 则水稻每公顷产量的年平均增长率是 .18. 如图,已知一次函数 的图像经过点A(5,0)与B(0,-4),那么关于 的不等式 ﹤0的解集是 .
17. 青山村种植水稻2019年平均每公顷产 , 2021年平均每公顷产 , 则水稻每公顷产量的年平均增长率是 .18. 如图,已知一次函数 的图像经过点A(5,0)与B(0,-4),那么关于 的不等式 ﹤0的解集是 . 19. 已知,在中, , 高 , 则边长为 .20. 如图,正方形中,点E在上,点F在上, , 连接交于点G,若 , 则的长是 .
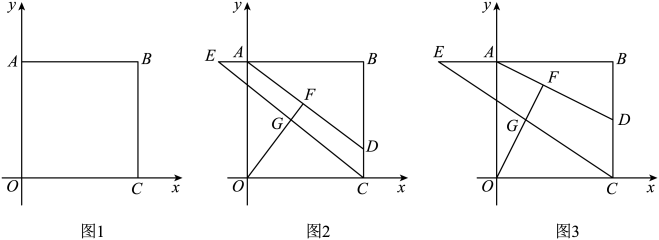
19. 已知,在中, , 高 , 则边长为 .20. 如图,正方形中,点E在上,点F在上, , 连接交于点G,若 , 则的长是 .
三、解答题
-
21. 解下列一元二次方程:(1)、x2+x=0;(2)、x2﹣4x﹣7=0.22. 图1、图2分别是的网格,网格中每个小正方形的边长均为1,线段的端点在小正方形的顶点上,请在图1、图2中各取一顶点(顶点必须在小正方形的顶点上),并且分别满足以下要求:
 (1)、在图1中画一个以线段为一边的直角 , 且的面积为10;(2)、在图2中画一个以线段为一边的钝角等腰 , 请直接写出线段的长.23. 某单位有一块四边形的空地,∠B=90°,量得各边的长度如图(单位:米),现计划在空地内种草,若每平方米草地造价30元,这块地全部种草的费用是多少元?
(1)、在图1中画一个以线段为一边的直角 , 且的面积为10;(2)、在图2中画一个以线段为一边的钝角等腰 , 请直接写出线段的长.23. 某单位有一块四边形的空地,∠B=90°,量得各边的长度如图(单位:米),现计划在空地内种草,若每平方米草地造价30元,这块地全部种草的费用是多少元? 24. 如图,已知CD为△ABC中线,E为CD上一点,连接AE并延长至点F,使 , 连接BF、CF, .
24. 如图,已知CD为△ABC中线,E为CD上一点,连接AE并延长至点F,使 , 连接BF、CF, . (1)、求证:四边形DBFC是平行四边形.(2)、设四边形ABFC的面积为S,在不添加任何辅助线的情况下,请写出图中四个面积等于的三角形.25. 为积极响应新旧动能转换,提高公司经济效益,某科技公司近期研发出一种新型高科技设备,经过市场调研发现,每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价x(单位:万元)成一次函数关系 .(1)、求年销售量y与销售单价x的函数关系式;(2)、已知每台设备成本价为30万元,根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润,则该设备的销售单价应是多少万元?
(1)、求证:四边形DBFC是平行四边形.(2)、设四边形ABFC的面积为S,在不添加任何辅助线的情况下,请写出图中四个面积等于的三角形.25. 为积极响应新旧动能转换,提高公司经济效益,某科技公司近期研发出一种新型高科技设备,经过市场调研发现,每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价x(单位:万元)成一次函数关系 .(1)、求年销售量y与销售单价x的函数关系式;(2)、已知每台设备成本价为30万元,根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润,则该设备的销售单价应是多少万元?