黑龙江省哈尔滨市道里区2021-2022学年八年级下学期期末数学试题
试卷更新日期:2023-05-05 类型:期末考试
一、单选题
-
1. 直角三角形的两条直角边长分别为3,4,则直角三角形的斜边长是( ).A、3 B、4 C、5 D、3或4
-
2. 由下列三条线段组成的三角形,不能构成直角三角形的是( ).A、1, , 2 B、1,1, C、7,24,25 D、5,11,12
-
3. 下列在平面直角坐标系中的曲线表示y是x的函数图象是( ).A、
 B、
B、 C、
C、 D、
D、
-
4. 已知正比例函数 , 若y随x的增大而减小,则k的取值范围是( ).A、 B、 C、 D、
-
5. 如图,在ABCD中 , 则∠B的度数是( ).
 A、 B、 C、 D、
A、 B、 C、 D、 -
6. 下列命题中,逆命题是真命题的是( ).A、菱形是对角线互相垂直的四边形 B、矩形既是轴对称图形,又是中心对称图形 C、正方形是对角线互相垂直且相等的四边形 D、平行四边形是对角线互相平分的四边形
-
7. 如图,在Rt△ABC中, , AC=5,BC=12,D为AB的中点,则CD的长为( )
 A、2.5 B、5 C、6 D、6.5
A、2.5 B、5 C、6 D、6.5 -
8. 关于x的一元二次方程有两个不相等的实数根,则实数m的取值范围为( )A、 B、 C、 D、
-
9. 正比例函数的函数值y随x的增大而增大,则一次函数的图像大致是( )A、
 B、
B、 C、
C、 D、
D、
-
10. 已知小明家、体育场、超市在一条笔直的公路旁(小明家、体育场、超市到公路的距离忽略不计),图中的信息反映的过程是小明从家跑步去体育场,在体育场锻炼了一阵后又走到超市买些学习用品,然后再走回家.图中x表示小明所用的时间,y表示小明离家的距离.根据图中的信息,下列说法中错误的是( ).
 A、体育场离小明家的距离是 B、小明在体育场锻炼的时间是 C、小明从体育场出发到超市的平均速度是 D、小明从超市回家的平均速度是
A、体育场离小明家的距离是 B、小明在体育场锻炼的时间是 C、小明从体育场出发到超市的平均速度是 D、小明从超市回家的平均速度是
二、填空题
-
11. 一次函数 , 当时,则y= .
-
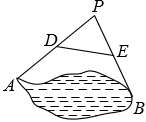
12. 如图,为测量池塘边A,B两点的距离,小军在池塘的一侧选取一点P,测得PA,PB的中点分别是D、E,且DE的长为16米,则A,B间的距离为米.
-
13. 将一次函数 的图象向上平移3个单位,所得的直线不经过第象限.
-
14. 已知一元二次方程kx2﹣9x+8=0的一个根为1,则k的值为 .
-
15. 如果菱形的两条对角线长为 与 ,则此菱形的面积
-
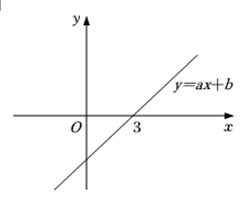
16. 如图,已知函数的图象与轴的交点坐标为 , 则根据图象可得不等式的解集是 .
-
17. 如图,在矩形ABCD中,AB=8,AD=10,点E为DC边上的一点,将△ADE沿直线AE折叠,点E刚好落在BC边上的点F处,则CE的长是 .

-
18. 在“绿色低碳,节能先行”的倡导下,自行车正逐渐成为人们喜爱的交通工具,据统计,某商城4月份销售自行车100辆,6月份销售了121辆.若该商城2022年4-6月的自行车销量的月平均增长率相同,则商城自行车销量的月平均增长率为 .
-
19. 在矩形ABCD中,CE平分∠BCD,交直线AD于点E,若CD=8,AE=4,则AC的长为 .
-
20. 如图,在△ABC中,AB=AC,BD⊥AC于点D,把线段AC绕点C旋转得到线段CE,点E恰好落在AB的延长线上, , △BCD的面积是8,则BC的长为 .

三、解答题
-
21. 解下列方程:(1)、;(2)、 .
-
22. 图1,图2中的小正方形的边长均为1,线段AB,EF的端点A,B,E,F均在小正方形的顶点上.
 (1)、在图1中画出一个以线段AB为边的平行四边形ABCD,点C,D均在小正方形的顶点上,且平行四边形ABCD的面积为8;(2)、在图2中画出以线段EF为边的菱形EFGH,点G,H均在小正方形的顶点上,且菱形EFGH的面积为8,连接FH,直接写出FH的长.
(1)、在图1中画出一个以线段AB为边的平行四边形ABCD,点C,D均在小正方形的顶点上,且平行四边形ABCD的面积为8;(2)、在图2中画出以线段EF为边的菱形EFGH,点G,H均在小正方形的顶点上,且菱形EFGH的面积为8,连接FH,直接写出FH的长. -
23. 如图,已知一次函数的图像经过点A(1,3)和B(-1,7),图像与x轴,y轴的交点分别为C,D两点.
 (1)、求这个一次函数的解析式;(2)、求△COD的面积.
(1)、求这个一次函数的解析式;(2)、求△COD的面积. -
24. 如图,点E,F在AC上, , , .
 (1)、求证:四边形BEDF是平行四边形;(2)、直接写出图中所有相等的线段(除外).
(1)、求证:四边形BEDF是平行四边形;(2)、直接写出图中所有相等的线段(除外). -
25. “人与自然和谐共生”哈尔滨湿地节系列活动中,某景点接待游客逐渐增多,6月份第一周接待游客200人,第三周接待游客288人,若该景点接待游客数量的周平均增长率相同.(1)、求该景点在6月份的第二周接待游客多少人?(2)、该景点第四周接待游客数量是第二周接待游客数量的1.8倍,平均每位游客购买1件旅游纪念品.该景点只销售A,B两种旅游纪念品,A种纪念品每件利润5元,B种纪念品每件利润8元,且售出的B种纪念品的数量不多于A种纪念品的3倍,设第四周该景点售出A种旅游纪念品a件,获得的总利润为W元,求W与a的函数关系式,并求出获得的最大利润.
-
26. 在平面直角坐标系中,点O为坐标原点,点A(a,0),点B(0,b),a,b是一元二次方程的两个解,且 .
 (1)、求直线AB的解析式;(2)、以OB为边作正方形OBCD,点C在第一象限,有一点P以每秒1个单位长度的速度从点D出发,沿着折线DC-CB-BO运动,到点O停止运动,设△POA的面积为S,点P的运动时间为t,求S与t的函数关系式,并直接写出自变量t的取值范围;(3)、在(2)的条件下,连接OP与AB交于点Q,当t为何值时, , 并求出此时点Q的坐标.
(1)、求直线AB的解析式;(2)、以OB为边作正方形OBCD,点C在第一象限,有一点P以每秒1个单位长度的速度从点D出发,沿着折线DC-CB-BO运动,到点O停止运动,设△POA的面积为S,点P的运动时间为t,求S与t的函数关系式,并直接写出自变量t的取值范围;(3)、在(2)的条件下,连接OP与AB交于点Q,当t为何值时, , 并求出此时点Q的坐标. -
27. 菱形ABCD的对角线AC,BD交于点O,以OA为边作矩形AEFO,点E恰好落在线段AB的垂直平分线上,点F在OB上,G是OD上一点,且OG=BF,连接CG,BF.
 (1)、如图1,求证:OB=OG+CG;(2)、如图2,M为菱形外一点,连接MA与BD交于点N,与BC交于点P.连接MC,MB, 若 , 求证:;(3)、如图3,在(2)的条件下,若 , , 连接MG,求线段MG的长.
(1)、如图1,求证:OB=OG+CG;(2)、如图2,M为菱形外一点,连接MA与BD交于点N,与BC交于点P.连接MC,MB, 若 , 求证:;(3)、如图3,在(2)的条件下,若 , , 连接MG,求线段MG的长.
