黑龙江哈尔滨市阿城区2021-2022学年八年级下学期期末考试数学试题

试卷更新日期：2023-05-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式中是最简二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{2}$ C、 $\sqrt{\frac{5}{2}}$ D、 $\sqrt{4}$

查看试题解析
2. 使 $\sqrt{x - 3}$ 有意义的x的取值范围是（）

A、x≤3 B、x＜3 C、x≥3 D、x＞3

查看试题解析
3. 一次函数y=x+2的图象与y轴的交点坐标为（）

A、(0，2) B、(0，-2) C、(2，0) D、(-2，0)

查看试题解析
4. 已知一组数据2、2、8、5、5、2．那么这组数据的众数是（）

A、8 B、6.5 C、5 D、2

查看试题解析
5. 下列各组线段能构成直角三角形的是（）

A、1，2，3 B、3，4，5 C、 $\sqrt{2} ， \sqrt{3} ， \sqrt{6}$ D、 $1 ， \sqrt{2} ， 3$

查看试题解析
6. 下列运算正确的是（）

A、 $\sqrt{2}$ + $\sqrt{3}$ = $\sqrt{5}$ B、 $\sqrt{18}$ =2 $\sqrt{3}$ C、 $\sqrt{2}$ • $\sqrt{3}$ = $\sqrt{5}$ D、 $\sqrt{2}$ ÷ $\sqrt{\frac{1}{2}}$ =2

查看试题解析
7. 直线y=2x向下平移2个单位长度得到的直线是（）

A、y=2（x+2） B、y=2（x﹣2） C、y=2x﹣2 D、y=2x+2

查看试题解析
8. 如图，菱形ABCD的对角线AC，BD的长分别是6和8，则这个菱形的面积是（　　）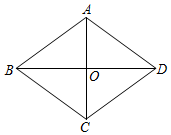

A、20 B、24 C、40 D、48

查看试题解析
9. 下列命题是真命题的是（）

A、两组对边分别平行的四边形是平行四边形 B、矩形的对角线互相垂直 C、对角线互相垂直平分的四边形是正方形 D、菱形的对角线相等

查看试题解析
10. 乐乐和壮壮分别从学校和图书馆同时出发，沿同一条相向而行，乐乐开始跑步中途改为步行，到达图书馆恰好用时30分钟．壮壮骑自行车以300米/分的速度直接回学校，两人离学校的路程y（米）与各自离开出发地的时间x（分）之间的函数图象如图所示，下列说法错误的是（）

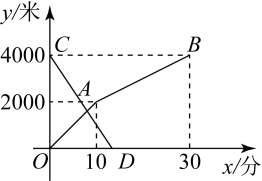A、学校与图书馆之间的路程为4000米 B、乐乐步行的速度为200米/分 C、壮壮离学校的路程y关于x的函数解析式为 $y = - 300 x + 4000 (0 \leq x \leq \frac{40}{3})$ D、两人第8分钟相遇

查看试题解析

二、填空题

11. 函数 $y = \frac{2 x}{x + 1}$ 中，自变量 $x$ 的取值范围是．

查看试题解析
12. 计算 $\sqrt{6} \times \sqrt{\frac{1}{3}}$ 的结果是．

查看试题解析
13. 计算 $\sqrt{24} + \sqrt{6}$ 的结果是．

查看试题解析
14. 直线 $y = 6 x + 1$ 与直线 $y = k x + 8$ 平行，则k= ．

查看试题解析
15. 已知直角三角形的两边长分别为5和12，则斜边长是

查看试题解析
16. 如图，矩形ABCD的对角线AC与BD相交点O，AC＝10，P、Q分别为AO、AD的中点，则PQ的的长度为.

查看试题解析
17. 若一次函数 $y = (k - 2) x + 1$ 的函数值y随x的增大而增大，则k的取值范围是.

查看试题解析
18. 如图，在 $▱ A B C D$ 中，点O是对角线 $A C 、 B D$ 的交点， $A C$ 垂直于 $B C$ ，且 $A C = 6 c m ， A D = 8 c m$ ，则 $O B =$ $c m$ ．

查看试题解析
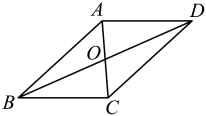19. 在等腰直角三角形ABC中，∠ACB=90°，AC=3，点P为边BC的三等分点，连接AP，则AP的长为．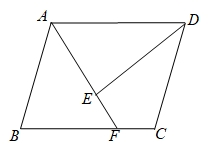

查看试题解析
20. 如图，在 $▱ A B C D$ 中，点F在 $B C$ 边上，连接 $A F$ ，点E在 $A F$ 上，连接 $D E$ ． $∠ D A E = 60 °$ ， $A F = B C$ ， $∠ B A F = ∠ A D E$ ，若 $A E = 5 ， C D = 7$ ，则 $C F$ 的长为．

查看试题解析

三、解答题

21. 先化简，再求值： $\frac{1 - 2 x}{2 x^{2} - 2 x} + \frac{1}{x - 1} + 1$ ，其中 $x = \sqrt{27} - 3 \sqrt{\frac{1}{3}}$ ．

查看试题解析
22. 如图方格纸中每个小正方形的边长均为1，线段 $A B$ ， $A E$ 的端点均在小正方形的顶点上．

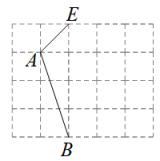(1)、在图中画出一个以 $A B$ 为一边的正方形 $A B C D$ ，且点C、点D均在小正方形顶点上；

(2)、在图中画出一个以 $A B 、 A E$ 为邻边的平行四边形 $E A B M$ ，且点M在小正方形的顶点上，连接 $D M$ 并直接写出线段 $D M$ 的长．

查看试题解析
23. 中华文明，源远流长：中华汉字，寓意深广，为了传承优秀传统文化，云扬中学团委组织了一次全校1800名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解本次大赛的成绩分布情况，随机抽取了部分学生的成绩（成绩取整数，总分100分）作为样本进行整理，得到下列不完整的统计图表：
组别
成绩x（分）
频数
百分比
A
$50 \leq x < 60$
10
$5 %$
B
$60 \leq x < 70$
20
C
$70 \leq x < 80$
30
D
$80 \leq x < 90$
E
$90 \leq x \leq 100$
80
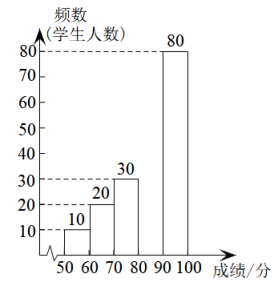
请根据所给信息，解答下列问题：

(1)、求抽样调查的学生有多少人，并补全频数分布直方图；

(2)、这次抽样调查的成绩的中位数落在组（填“A，B，C，D或E”）；

(3)、若成绩在90分以上（包括90分）的为“优”等，估计该校参加这次比赛的学生中成绩“优”等的有多少人？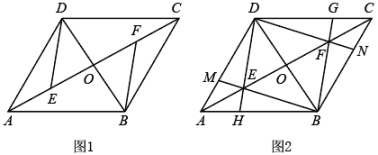

查看试题解析
24. 在四边形 $A B C D$ 中，对角线 $A C 、 B D$ 交于点O， $O A = O C$ ， $O B = O D$ ，点E是 $O A$ 中点，点F是 $O C$ 中点，连接 $D E 、 B F$ ．

(1)、如图1，求证： $D E = B F$ ；

(2)、如图2，延长 $D E 、 B F$ 分别交 $A B 、 C D$ 边于点H、G，连接 $B E$ 并延长交 $A D$ 于点M，连接 $D F$ 并延长交 $B C$ 于点N，在不添加任何辅助线的情况下，直接写出图2中所有的平行四边形．

查看试题解析
25. 云扬中学体育社团计划购买排球、篮球，已知购买1个排球与1个篮球的总费用为180元；3个排球与2个篮球的总费用为420元．

(1)、求购买1个排球、1个篮球的费用分别是多少元？

(2)、若该社团计划购买此类排球和篮球共60个，并且篮球的数量大于排球数量的2倍，设购买m个排球，购买的总费用为w元．求w关于m的函数解析式，并求出购买多少个排球，使购买的总费用最少，总费用最少是多少元？

查看试题解析
26. 如图，在四边形 $A B C D$ 中， $A B ∥ C D ， ∠ D A B = ∠ B C D$ ．

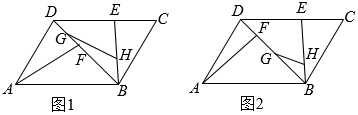(1)、如图1，求证：四边形 $A B C D$ 是平行四边形；

(2)、如图1，连接 $B D$ ，射线 $B A$ 沿 $B D$ 翻折交 $C D$ 边于点E，点F，G在 $B D$ 上，点H在 $B E$ 上，连接 $A F 、 G H$ ，若 $∠ A B C = ∠ B H G = 2 ∠ B C D$ ， $A D = A F$ 求证： $∠ B A F = 2 ∠ B G H$ ；

(3)、如图2，在（2）的条件下，G为 $B D$ 中点，若 $B H = 1$ ， $A F = 4$ ，求 $C E$ 的长．

查看试题解析
27. 如图，在平面直角坐标系中，直线 $y = \frac{4}{3} x + 8$ 与x轴、y轴分别交于A、B两点，点C为x轴正半轴上一点， $A B = A C$ ，作直线 $B C$ ．

(1)、求 $A B$ 的长；

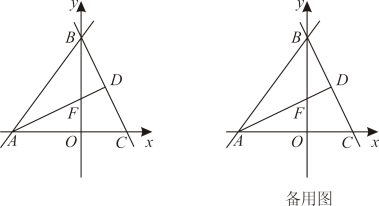(2)、 $A D$ 是 $△ A B C$ 的中线，交y轴于点F，求直线 $A D$ 的解析式；

(3)、在（2）的条件下，点E在 $A F$ 上，点G在 $C D$ 上，且 $C G = A E$ ，连接 $E G$ ， $△ E G M$ 是以 $E G$ 为斜边的等腰直角三角形，点M位于直线 $A D$ 的上方，作点M关于直线 $E G$ 的对称点N，连接 $N C 、 N E 、 N G$ ， $M G$ 与 $A D$ 相交于点H，当 $∠ N C D = 90 °$ 时，求点H的坐标．

查看试题解析

组别	成绩x（分）	频数	百分比
A	$50 \leq x < 60$	10	$5 %$
B	$60 \leq x < 70$	20
C	$70 \leq x < 80$	30
D	$80 \leq x < 90$
E	$90 \leq x \leq 100$	80