安徽省铜陵市铜官区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2023-05-05 类型：期末考试

进入出卷网下载

一、单选题

1. 若二次根式 $\sqrt{4 - 2 x}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x \leq 2$ B、 $x \geq 2$ C、 $x > 2$ D、 $x > - 2$

查看试题解析
2. 下列命题中错误的是（）

A、菱形的对角线互相垂直 B、两组对边分别相等的四边形是平行四边形 C、矩形的对角线相等 D、对角线相等的四边形是正方形

查看试题解析
3. 已知一次函数 $y = k x + 6$ 的图象经过 $A (2 ， - 2)$ ，则 $k$ 的值为（）

A、 $- 4$ B、 $- 1$ C、 $1$ D、 $4$

查看试题解析
4. 一次数学测试后，某小组五名同学的成绩及数据分析如下表所示（有两个数据被遮盖），那么被遮盖的两个数据依次是（）．

甲

乙

丙

丁

戊

方差

平均成绩

81

79

■

80

82

■

80

A、78， $\sqrt{2}$ B、78，2 C、80， $\sqrt{2}$ D、80，2

查看试题解析
5. 如图，在Rt△ABC中，∠A=90°，AB=6，AC=8，现将Rt△ABC沿BD进行翻折，使点A刚好落在BC上，则CD的长为（）

A、10 B、5 C、4 D、3

查看试题解析
6. 两条直线y₁＝kx﹣k与y₂＝﹣x在同一平面坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
7. 勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载。如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积，则一定能求出（）

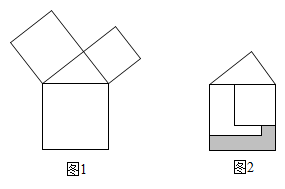A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和

查看试题解析
8. 如图，直线y＝kx+b（b＞0）经过点（2，0），则关于x的不等式kx+b＞0的解集是（）

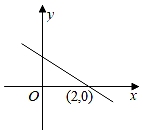A、x＞2 B、x＜2 C、x≥2 D、x≤2

查看试题解析
9. 如图，在直角三角形 $A B C$ 中， $∠ A C B = 90 °$ ， $A C = 3$ ， $B C = 4$ ，点M是边 $A B$ 上一点（不与点A，B重合），作 $M E ⊥ A C$ 于点E， $M F ⊥ B C$ 于点F，若点P是 $E F$ 的中点，则 $C P$ 的最小值是（）

A、1.2 B、1.5 C、2.4 D、2.5

查看试题解析
10. 在平面直角坐标系中，直线 $l ： y = x - 1$ 与x轴交于点 $A_{1}$ ，如图所示依次作正方形 $A_{1} B_{1} C_{1}$ O、正方形 $A_{2} B_{2} C_{2} C_{1}$ 、…、正方形 $A_{n} B_{n} C_{n} C_{n - 1}$ 使得点 $A_{1} 、 A_{2} 、 A_{3}$ 、…在直线l上，点 $C_{1} 、 C_{2} 、 C_{3}$ 、…在y轴正半轴上．点 $B_{2022}$ 的坐标是（）

A、 $(2^{2021} ， 2^{2022} - 1)$ B、 $(2^{2022} ， 2^{2021} - 1)$ C、 $(2^{2021} ， 2^{2021} - 1)$ D、 $(2^{2022} ， 2^{2022} - 1)$

查看试题解析

二、填空题

11. 已知一组数据 $x_{1} ， x_{2} ， x_{3}$ 的平均数是15，方差是1，那么另一组数据 $2 x_{1} - 4$ ， $2 x_{2} - 4 ， 2 x_{3} - 4$ 的平均数是．

查看试题解析
12. 在① $\sqrt{14}$ ；② $\sqrt{a^{2} + b^{2}}$ ；③ $\sqrt{27}$ ；④ $\sqrt{m^{2} + 1}$ 中，最简二次根式有个．

查看试题解析
13. 在平面直角坐标系中，将一条直线向下平移3个单位长度，再向右平移2个单位长度，得到直线 $y = 2 x - 6$ ，则平移前的直线解析式为：．

查看试题解析
14. 对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形ABCD，对角线AC、BD交于点O．若AD=3，BC=5，则 $A B^{2} + C D^{2} =$ ．

查看试题解析
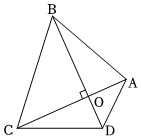15. 如图，在△ABC中，∠ACB＝90°，AC＝2，D是边AB的中点，E是边BC上一点．若DE平分△ABC的周长，则DE的长是

查看试题解析

三、解答题

16. 计算：

(1)、 $4 \sqrt{5} + \sqrt{45} - \sqrt{8} + 4 \sqrt{2}$

(2)、 $\sqrt{\frac{1}{2}} \times \sqrt{48} \div \sqrt{\frac{1}{8}}$

查看试题解析
17. 一次函数的图象与x轴交于点 $A (1 ， 0)$ ，与y轴交于点 $B (0 ， - 2)$ ．

(1)、求一次函数的函数解析式，并在所给的坐标系中画出图象．

(2)、若直线 $A B$ 上有一点C，且 $△ B O C$ 的面积为2，求点C的坐标；

查看试题解析
18. 如图是一块地，已知AD=4m，CD=3m，AB=13m，BC=12m，且CD⊥AD，求这块地的面积．

查看试题解析
19. 为转变教育管理方式并为学校教育教学提供参考，某区随机抽取八年级若干名学生参加2021年国家义务教育质量检测，并将测试中的数学成绩a（分数）分成A，B，C，D，E五个等级（A：90≤a≤100，B：80≤a＜90，C：70≤a＜80，D：60≤a＜70，E：a＜60），绘制出了如图两幅不完整的统计图，根据以上信息，回答下列问题：

(1)、直接写出抽查的学生人数，及m=；

(2)、请补全条形统计图，该组数据的中位数在等级；

(3)、若该区八年级共有学生8000人，数学成绩a≥80为优秀，请估计该区八年级数学成绩达到优秀的约有多少人？

查看试题解析
20. 如图1，矩形ABCD中，AB=2，BC=3，过对角线AC中点O的直线分别交边BC、AD于点E、F

(1)、求证：四边形AECF是平行四边形；

(2)、如图2，当EF⊥AC时，求EF的长度．

查看试题解析
21. 在抗疫期间，某药房销售A、B两种型号的口罩，已知销售800只A型口罩和450只B型口罩共获利2100元，销售400只A型口罩和600只B型口罩共获利1800元．

(1)、每只A型口罩和B型口罩分别可获利多少元？

(2)、药房计划购进A型、B型口罩共2000只，设购进A型口罩x只，这2000只口罩的总利润为y元，
①求y关于x的函数关系式，并写出自变量的取值范围；
②根据市场需求，B型口罩的数量不得超过A型数量的3倍，且不少于A型口罩的数量，药房应购进A、B型口罩各多少只才能获得最大利润？最大利润为多少元？

查看试题解析
22. 阅读下列一段文字，然后回答下列问题．
已知在平面内有两点 $P_{1} (x_{1} ， y_{1})$ 、 $P_{2} (x_{2} ， y_{2})$ ，其两点间的距离 $P_{1} P_{2} = \sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$ ，同时，当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时，两点间距离公式可化简为 $| x_{1} - x_{2} |$ 或 $| y_{1} -$ $y_{2} |$ .

(1)、已知 $A (2 ， 4)$ 、 $B (- 3 ， - 8)$ ，试求A、B两点间的距离.
已知M、N在平行于y轴的直线上，点M的纵坐标为4，点N的纵坐标为-1，试求M、N两点的距离为；

(2)、已知一个三角形各顶点坐标为 $D (1 ， 6)$ 、 $E (- 3 ， 3)$ 、 $F (4 ， 2)$ ，你能判定此三角形的形状吗?说明理由．

(3)、在（2）的条件下，平面直角坐标系中，在x轴上找一点P，使 $P D + P F$ 的长度最短，求出点P的坐标及 $P D + P F$ 的最短长度．

查看试题解析

甲	乙	丙	丁	戊	方差	平均成绩
81	79	■	80	82	■	80