安徽省宿州市萧县2021-2022学年八年级下学期期末数学试题
试卷更新日期:2023-05-05 类型:期末考试
一、单选题
-
1. 下列四个图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、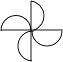 2. 不等式的解集在数轴上表示为( )A、
2. 不等式的解集在数轴上表示为( )A、 B、
B、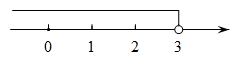 C、
C、 D、
D、 3. 下列从左到右的变形,是分解因式的是( )A、xy2(x-1)=x2y2-xy2 B、2a2+4a=2a(a+2) C、(a+3)(a-3)=a2-9 D、x2+x-5=(x-2)(x+3)+14. 下列运算正确的是( )A、-=1 B、 C、 D、5. 一个多边形的每个内角均为120°,则这个多边形是( )A、七边形 B、六边形 C、五边形 D、四边形6. 若实数 、 满足 , ,则 的值是( )A、-2 B、2 C、-50 D、507. 平行四边形的周长为 , 相邻两边的差为 , 则平行四边形的各边长为( )A、 , , , B、 , , , C、 , , , D、 , , ,8. 如图,将△OAB绕点O逆时针旋转80°,得到△OCD.若∠A=2∠D=100°,则∠α的度数是( )
3. 下列从左到右的变形,是分解因式的是( )A、xy2(x-1)=x2y2-xy2 B、2a2+4a=2a(a+2) C、(a+3)(a-3)=a2-9 D、x2+x-5=(x-2)(x+3)+14. 下列运算正确的是( )A、-=1 B、 C、 D、5. 一个多边形的每个内角均为120°,则这个多边形是( )A、七边形 B、六边形 C、五边形 D、四边形6. 若实数 、 满足 , ,则 的值是( )A、-2 B、2 C、-50 D、507. 平行四边形的周长为 , 相邻两边的差为 , 则平行四边形的各边长为( )A、 , , , B、 , , , C、 , , , D、 , , ,8. 如图,将△OAB绕点O逆时针旋转80°,得到△OCD.若∠A=2∠D=100°,则∠α的度数是( )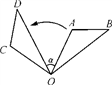 A、50° B、60° C、40° D、30°9. 如图,在中, , , , 的垂直平分线交于点M,交于点E,的垂直平分线交于点N,交于点F,则的长为( )
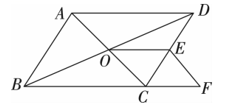
A、50° B、60° C、40° D、30°9. 如图,在中, , , , 的垂直平分线交于点M,交于点E,的垂直平分线交于点N,交于点F,则的长为( )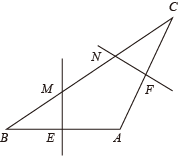 A、 B、 C、 D、10. 如图所示,在四边形中, , 对角线 , 相交于点O,于点E,于点F,连接 , , 若 , 则下列结论:①;②;③四边形是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是( )
A、 B、 C、 D、10. 如图所示,在四边形中, , 对角线 , 相交于点O,于点E,于点F,连接 , , 若 , 则下列结论:①;②;③四边形是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是( )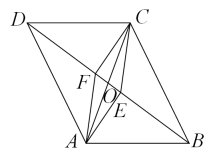 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
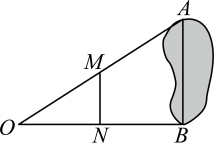
11. “等边对等角”的逆命题是.12. 如图所示,小明为了测量学校里一池塘的宽度 , 选取可以直达A,B两点的点O处,再分别取 , 的中点M,N,量得 , 则池塘的宽度AB为m.
 13. 因式分解: .14. 如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是 度.
13. 因式分解: .14. 如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是 度.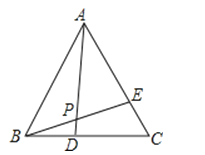 15. 如图,已知函数和的图象交点为P,则不等式的解集为 .
15. 如图,已知函数和的图象交点为P,则不等式的解集为 .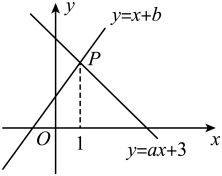 16. 如图,点A,E,F,C在一条直线上,若将的边沿方向平移,平移过程中始终满足下列条件: , 于点E,于点F,且 . 则当点E,F不重合时,与的关系是 .
16. 如图,点A,E,F,C在一条直线上,若将的边沿方向平移,平移过程中始终满足下列条件: , 于点E,于点F,且 . 则当点E,F不重合时,与的关系是 .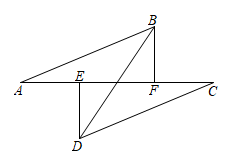
三、解答题