安徽省合肥市庐阳区2021-2022学年八年级下学期期末数学试题

试卷更新日期：2023-05-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列式子是最简二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{6}$ C、 $\sqrt{8}$ D、 $\sqrt{12}$

查看试题解析
2. 六边形的内角和是（）

A、540° B、720° C、900° D、1080°

查看试题解析
3. 用配方法解方程 $x^{2} + 4 x + 2 = 0$ 时，配方结果正确的是（）

A、 ${(x + 2)}^{2} = 2$ B、 ${(x - 2)}^{2} = 2$ C、 ${(x + 2)}^{2} = 6$ D、 ${(x - 2)}^{2} = 6$

查看试题解析
4. 下列各组数据为边，不能组成直角三角形的是（　　）

A、1，2， $\sqrt{7}$ B、 $\sqrt{2}$ ， $\sqrt{3}$ ， $\sqrt{5}$ C、5，12，13 D、2，2， $2 \sqrt{2}$

查看试题解析
5. 下列说法正确的是（）

A、一组对边相等，另一组对边平行的四边形是平行四边形 B、有一个角是直角的平行四边形是矩形 C、对角线互相垂直且平分的四边形是正方形 D、对角线互相垂直的四边形是菱形

查看试题解析
6. 由于疫情得到缓和，餐饮行业逐渐回暖，某地一家餐厅重新开张，开业第一天收入约为5000元，之后两天的收入按相同的增长率增长，第3天收入约为6050元，若设每天的增长率为x，则x满足的方程是（）

A、5000（1+x）＝6050 B、5000（1+2x）＝6050 C、5000（1﹣x）²＝6050 D、5000（1+x）²＝6050

查看试题解析
7. 已知一组数据3，6，x，5，5，7的平均数是5，则这组数据的方差是（）

A、1 B、 $\frac{5}{3}$ C、2 D、 $\frac{7}{3}$

查看试题解析
8. 如图，点E为正方形ABCD边BC延长线上一点，且 $C E = B D$ ， AE交DC于点F， $∠ A F C$ 的度数为（）

A、 $122.5 °$ B、 $112.5 °$ C、 $135 °$ D、 $125 °$

查看试题解析
9. 如图，在△ABC中，点D，E，F分别是AB，BC，AC的中点，则下列四个判断中不一定正确的是（　　）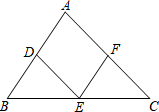

A、四边形ADEF一定是平行四边形 B、若∠B+∠C=90°，则四边形ADEF是矩形 C、若四边形ADEF是菱形，则△ABC是等边三角形 D、若四边形ADEF是正方形，则△ABC是等腰直角三角形

查看试题解析
10. 如图，在 $△ A B C$ 中， $A E ⊥ B C$ 于点E， $B D ⊥ A C$ 于点D；点F是AB的中点，连接DF，EF，设 $∠ D F E = α$ ，则 $∠ C$ 的度数可表示为（）

A、 $α$ B、 $2 α$ C、 $90 ° - α$ D、 $90 ° - \frac{1}{2} α$

查看试题解析

二、填空题

11. 方程 $x^{2} - 9 = 0$ 的根是．

查看试题解析
12. 我们知道，正五边形不能进行平面镶嵌．如图，将三个全等的正五边形拼接在一起，则 $∠ 1$ 度数是．

查看试题解析
13. 若m，n是一元二次方程 $x^{2} + 2 x - 1 = 0$ 的两个实根，则 $m^{2} + 3 m + n$ 的值是．

查看试题解析
14. 如图，矩形纸片ABCD， $A B = 4$ ， $A D = 6$ ，点G是边AD上的点， $A G = 2$ ，点H是边BC上一点，将纸片沿GH折叠，A、B的对应点分别为E、F，

(1)、当点F落在边DC上时，CF长为；

(2)、CF最小值为．

查看试题解析

三、解答题

15. 计算： $\sqrt{48} \div \sqrt{3} + \sqrt{\frac{1}{2}} \times \sqrt{12} - \sqrt{24}$ .

查看试题解析
16. 解一元二次方程： ${(x - 3)}^{2} = 2 (x - 3)$ ．

查看试题解析
17. 如图，正方形网格中每个小正方形边长都是1，小正方形的顶点称为格点，在正方形网格中分别画出下列图形：

(1)、画出长为 $\sqrt{5}$ 的线段AB；

(2)、画出一个腰长为 $\sqrt{10}$ 、面积为3的等腰△DEF．

查看试题解析
18. 如图，小旭放风筝时，风筝挂在了树上，他先拉住风筝线，垂直于地面，发现风筝线多出1米；把风筝线沿直线BC向后拉5米，风筝线末端刚好接触地面，求风筝距离地面的高度AB.

查看试题解析
19. 已知关于的一元二次方程： $x^{2} + (k - 5) x + 4 - k = 0$ ；

(1)、求证：无论 $k$ 为何值，方程总有实数根；

(2)、若方程的一个根是2，求另一个根及 $k$ 的值.

查看试题解析
20. 如图，平行四边形ABCD，AC、BD相交于点O，点E在线段BC上， $A E = C E$ ，连接EO并延长交AD边于点F．

(1)、求证：四边形AECF为菱形；

(2)、若 $∠ A E C = 120 °$ ， $E F = 4$ ，直接写出菱形AECF的面积：．

查看试题解析
21. 2022年2月8日，中国选手谷爱凌在冬奥会自由式滑雪女子大跳台决赛中夺得金牌，国际滑联评价谷爱凌为滑雪史上第一人．已知自由式滑雪大跳台的计分规则如下：
①每次滑雪的动作，按照其完成难度的不同对应一个难度系数A；
②每次滑雪都有7名裁判进行打分，在7个得分中去掉1个最高分和1个最低分，剩下5个得分的平均值为这次起跳的完成分B；
③运动员该次滑雪的最后得分C＝难度系数A×完成分B×3．
在某次自由滑雪大跳台比赛中，某运动员的打分（满分10分）表为：
难度系数
裁判
1
2
3
4
5
6
7
3.0
打分
10
9.5
9
9
9.5
9
9

(1)、7名裁判打分的众数是；中位数是；

(2)、该运动员的最后得分是多少？

(3)、已知某运动员在一次滑雪大跳台比赛中完成了难度系数3.2的动作，且所有裁判都打了满分，请你帮她算一下，难度系数3.2的满分成绩应该是多少分？

查看试题解析
22. 某商店销售一种商品，每件进价60元，在销售过程中发现，当售价为100元时，每天可售出30件．该商店决定采取适当的降价措施，以扩大销售量增加利润．经调查发现，如果每件商品降价1元，平均可多售出3件．

(1)、若每件商品降价5元，商家平均每天能盈利多少元？

(2)、每件商品降价多少元时，能让利于顾客并且让商家平均每天能盈利1800元？

查看试题解析
23. 四边形ABCD与四边形DEFG均为正方形，M是BF的中点，连接CM、GM．

(1)、如图1，当点C在线段DG上时．
①猜想CM与GM的数量关系和位置关系；
②证明你猜想的结论；

(2)、如图2，当D、C、G三点不共线时，（1）中的结论还成立吗？说明理由．

查看试题解析

难度系数	裁判	1	2	3	4	5	6	7
3.0	打分	10	9.5	9	9	9.5	9	9