安徽省合肥市庐江县2021-2022学年八年级下学期期末数学试题

试卷更新日期：2023-05-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，最简二次根式是（）

A、 $\sqrt{8}$ B、 $\sqrt{11}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\sqrt{0.2}$

查看试题解析
2. 如图，在平行四边形ABCD中，∠A＝40°，则∠C大小为（）

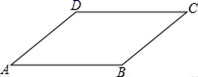A、40° B、80° C、140° D、180°

查看试题解析
3. 甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差的数值如下表：
选手
甲
乙
丙
丁
平均数
9.2
9.3
9.5
9.1
方差
0.035
0.015
0.025
0.027
则这四人中成绩发挥最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 将直线y＝x+5向下平移2个单位，得到的直线是（）

A、y＝x﹣2 B、y＝x+2 C、y＝x+3 D、y＝x+7

查看试题解析
5. 下列各组线段中，能够组成直角三角形的一组是（）

A、1，2，3 B、2，3，4 C、4，5，6 D、1， $\sqrt{3}$ ，2

查看试题解析
6. 点 $A (- 2 ， a)$ 与点B（2，b）都在直线 $y = - 3 x + 1$ 上，则（）

A、 $a > b$ B、 $a = b$ C、 $a < b$ D、无法比较

查看试题解析
7. 下列计算正确的是（）

A、 $\sqrt{6} \div 3 = \sqrt{2}$ B、 $\sqrt{5} + \sqrt{3} = \sqrt{8}$ C、 $\sqrt{2} \times \sqrt{5} = \sqrt{10}$ D、 $3 \sqrt{5} - \sqrt{2} = 2 \sqrt{3}$

查看试题解析
8. 在下列给出的条件中，能判定四边形ABCD为平行四边形的是（）

A、 $A B = B C$ ， $C D = D A$ B、 $A B = B C$ ， $A D / / B C$ C、 $∠ A = ∠ B$ ， $∠ C = ∠ D$ D、 $A B / / C D$ ， $∠ A = ∠ C$

查看试题解析
9. 如图， $O A = 5$ ，过点 $A$ 作直线 $l$ $⊥ O A$ ，点 $B$ 在直线 $l$ 上， $A B = 2$ ，以点 $O$ 为圆心，以 $O B$ 长为半径作弧，与 $O A$ 的延长线交于点 $C$ ，则点 $C$ 表示的实数是（）

A、 $\sqrt{21}$ B、 $\sqrt{29}$ C、7 D、29

查看试题解析
10. 如图，在平行四边形ABCD中，∠C＝120°，AD＝4，AB＝2，点H、G分别是边CD、BC上的动点．连接AH、HG，点E为AH的中点，点F为GH的中点，连接EF．则EF的最大值与最小值的差为（　　）

A、1 B、 $\sqrt{3} -$ 1 C、 $\frac{\sqrt{3}}{2}$ D、2 $- \sqrt{3}$

查看试题解析

二、填空题

11. 已知 $\sqrt{a + 2}$ 有意义，则a的取值范围为．

查看试题解析
12. 如图，在△ABC中，∠ACB＝90°，以它的三边为边分别向外作正方形，面积分别为S₁ ， S₂ ， S₃ ，已知S₁＝5，S₂＝12，则S₃＝．

查看试题解析
13. 如图，在Rt $△$ ABC中 $∠ A C B = 90^{\circ}$ ， $B C = 6$ ， $A C = 8$ ，D为AB的中点， $A E ∥ C D ， C E ∥ A B$ ，则四边形ADCE的周长为．

查看试题解析
14. 如图1．在正方形ABCD的边BC上有一点E，连接AE．点P从正方形的顶点A出发，沿A→D→C以1cm/s的速度匀速运动到点C．图2是点P运动时，△APE的面积 $y (c m^{2})$ 随时间x（s）变化的函数图象．

(1)、正方形ABCD的边长为．

(2)、当 $y = \frac{13}{2}$ 时，x的值为．

查看试题解析

三、解答题

15. 计算： $(\sqrt{6} - 2 \sqrt{3}) \times \sqrt{3} - 6 \sqrt{\frac{1}{2}}$

查看试题解析
16. 如图，正方形网格中每个小正方形边长都是1，小正方形的顶点称为格点，在正方形网格中分别画出下列图形：
( 1 )长为 $\sqrt{5}$ 的线段AB，且A，B为格点；
( 2 )边长为 $\sqrt{10}$ 、面积为6的菱形CDEF，且菱形CDEF的顶点均为格点．

查看试题解析
17. 某班将本校的办学理念“学会生活，学会学习，学会做人”做成宣传牌AB，放置在教室的黑板上方（如图所示），在一次活动中，小明搬来一架2.5米长的梯子AE，靠在宣传牌AB的顶部A处，底端落在地板E处，然后移动梯子使顶端落在宣传牌AB的底部B处，而底端E向外移了0.5米到C处（即CE=0.5米）．已知黑板的上边距地板高度BM=2米．求宣传牌的顶部A距地板的高度AM为多少米（结果保留根号）．

查看试题解析
18. 观察下列等式：
第1个等式： $\sqrt{1 + \frac{1}{3}} = \frac{2}{3} \sqrt{3}$ ；

第2个等式： $\sqrt{2 + \frac{1}{4}} = \frac{3}{4} \sqrt{4}$ ；

第3个等式： $\sqrt{3 + \frac{1}{5}} = \frac{4}{5} \sqrt{5}$ ；

第4个等式： $\sqrt{4 + \frac{1}{6}} = \frac{5}{6} \sqrt{6}$ ；

……；

按照以上规律，解决下列问题：

(1)、写出第5个等式：；

(2)、写出你猜想的第n个等式，并证明．

查看试题解析
19. 如图，已知四边形ABCD为平行四边形，AE，CF分别平分∠BAD和∠BCD，交BD于点E，F，连接AF，CE．

(1)、若∠BCF＝65°，求∠ABC的度数；

(2)、求证：四边形AECF是平行四边形．

查看试题解析
20. 如图，直线 $y = k x + b$ 经过点 $A (5 ， 0)$ ， $B (1 ， 4)$ ．

(1)、求直线 $A B$ 的解析式；

(2)、若直线 $y = 2 x - 4$ 与直线 $A B$ 相交于点C，求点C的坐标；

(3)、根据图象，写出关于x的不等式 $2 x - 4 \geq k x + b$ 的解集．

查看试题解析
21. 为宣传防护知识，增强免疫能力，某班举行了“防疫”知识测试，测试共10道题，以下是根据测试结果绘制的不完整的扇形统计图和条形统计图，请根据相关信息，解答下列问题：

(1)、图1中m的值为；

(2)、补全条形统计图；

(3)、求该班学生答对题数的平均数、众数和中位数．

查看试题解析

22. 甲市A，B两个蔬菜基地得知乙地C，D两个灾民安置点分别急需蔬菜240t和260t的消息后，决定调运蔬菜支援灾区，已知A蔬菜基地有蔬菜200t，B蔬菜基地有蔬菜300t，现将这些蔬菜全部调运C，D两个灾区安置点．从A地运往C，D两处的费用分别为每吨20元和25元，从B地运往C，D两处的费用分别为每吨15元和18元．设从B地运往C处的蔬菜为x吨．

(1)、请填写下表；

	C	D	总计/t
A			200
B	X	$300 - x$	300
总计/t	240	260	500

(2)、求两个蔬菜基地调运蔬菜的运费相等时x的值；

(3)、设A，B两个蔬菜基地的总运费为w元，求出w与x之间的函数关系式，并求总运费最小的调运方案．

查看试题解析

23. 如图①，在正方形ABCD中，E，F分别是边AD，CD上的点（点E，F不与端点重合），且AE=DF，BE，AF交于点P，过点C作CH⊥BE交BE于点H．

(1)、线段AF与BE的数量关系为，位置关系为．

(2)、若 $A B = 2 \sqrt{3}$ ， AE=2，求线段BH的长．

(3)、如图②，连接CP并延长交AD于点Q，若点H是BP的中点，求 $\frac{C P}{P Q}$ 的值．

查看试题解析

选手	甲	乙	丙	丁
平均数	9.2	9.3	9.5	9.1
方差	0.035	0.015	0.025	0.027