安徽省滁州市定远县吴圩片2021-2022学年八年级下学期期末数学试题

试卷更新日期：2023-05-05 类型：期末考试

进入出卷网下载

一、单选题

1. 使代数式 $\frac{\sqrt{1 - x}}{x + 1}$ 有意义的x的取值范围是（）

A、 $x \leq 1$ 且 $x \neq - 1$ B、 $x \leq 1$ 且 $x \neq 0$ C、 $x < 1$ 且 $x \neq - 1$ D、 $- 1 < x \leq 1$

查看试题解析
2. 已知 $y = \sqrt{x - 2} + \sqrt{2 - x} - \sqrt{3}$ ，则 $(x + y)^{2020} (x - y)^{2021}$ 的值为（）

A、 $2 - \sqrt{3}$ B、 $2 + \sqrt{3}$ C、 $- 1$ D、 $1$

查看试题解析
3. 一元二次方程 $2 x^{2} - (a + 1) x = x (x - 1) - 1$ 化成一般式后，二次项系数为1，一次项系数为-1，则a的值为（）

A、-1 B、1 C、-2 D、2

查看试题解析
4. 用配方法解一元二次方程x²-8x+5=0，将其化成（x+a）²=b的形式，则变形正确的是（）

A、（x+4）²=11 B、（x-4）²=21 C、（x-8）²=11 D、（x-4）²=11

查看试题解析
5. 盛夏来袭，为促进消费，瑶海万达广场从6月份开始对部分商品进行“折上折”（两次打折数相同）优惠活动，已知一件原价1000元的服装，优惠后实际仅需640元，设该服装原本打x折，则有（）

A、1000(1-2x)=640 B、1000(1-x)²=640 C、1000 ${(\frac{x}{10})}^{2}$ =640 D、1000 ${(1 - \frac{x}{10})}^{2}$ =640

查看试题解析
6. 勾股定理是人类最伟大的科学发现之一，在我国古算书（周髀算经）中早有记载；如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内若直角三角形两直角边分别为6和8，则图中阴影部分的面积为（）

A、20 B、24 C、28 D、无法求出

查看试题解析
7. 已知a，b，c是 $Δ A B C$ 的三边长，且满足 $\sqrt{a - 6} + | b - 8 | + {(c - 10)}^{2} = 0$ ，则 $Δ A B C$ 是（）

A、以a为斜边的直角三角形 B、以b为斜边的直角三角形 C、以c为斜边的直角三角形 D、以c为底边的等腰三角形

查看试题解析
8. 如图，在正六边形ABCDEF中，AC=2 $\sqrt{3}$ ，则它的边长是（）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、2

查看试题解析
9. 如图，在矩形 $A B C D$ 中， $A D = 1 ， A B = 2 \sqrt{2} ， M$ 为线段 $B D$ 上一动点， $M P ⊥ C D$ 于点 $P ， M Q ⊥ B C$ 于点Q，则 $P Q$ 的最小值为（）

A、 $\frac{3 \sqrt{2}}{2}$ B、 $\frac{2 \sqrt{2}}{3}$ C、 $\frac{\sqrt{2}}{3}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
10. 下表记录了某校4名同学游泳选拔赛成绩的平均数与方差：

队员1
队员2
队员3
队员4
平均数 $\overset{—}{x}$ （秒）
51
50
51
50
方差s²（秒²）
3.5
3.5
14.5
15.5
根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择（　　）

A、队员1 B、队员2 C、队员3 D、队员4

查看试题解析

二、填空题

11. 若 $\sqrt{{(x - 3)}^{2}} = 3 - x$ ，则x的取值范围是．

查看试题解析
12. 已知m²-2m-1=0，n²-2n-1=0且m $\neq$ n ，则 $\frac{n}{m} + \frac{m}{n}$ 的值为．

查看试题解析
13. 在《九章算术》中有一个问题（如图)：今有竹高一丈，末折抵地，去本三尺，问折者高几何?它的意思是：一根竹子原高一丈（ $10$ 尺)，中部一处折断，竹梢触地面处离竹根 $3$ 尺，试问折断处离地面尺．

查看试题解析
14. 如图所示， $∠ M A N = 9 0^{∘}$ ，点C在边 $A M$ 上， $A C = 4$ ， B为边 $A N$ 上一动点，连接 $B C$ ， $Δ G B C$ 和 $Δ A B C$ 关于 $B C$ 所在直线对称， $D 、 E$ 分别为 $A C$ 、 $B C$ 的中点，连接 $D E$ 并延长交 $G B$ 所在直线于点F，连接 $G E$ ．当 $Δ G E F$ 为直角三角形时， $A B$ 的长为．

查看试题解析

三、解答题

15. 计算： $| - \sqrt{3} | - (4 - π)^{0} - \sqrt{24} \div \sqrt{8} + {(\frac{1}{4})}^{- 1}$

查看试题解析
16. 解方程：(x-3)²＝2x-6

查看试题解析
17. 在进行二次根式的运算时，如遇到 $\frac{1}{\sqrt{2} + 1}$ 这样的式子，我们可以按如下两种方法进行化简：
方法一： $\frac{1}{\sqrt{2} + 1} = \frac{\sqrt{2} - 1}{(\sqrt{2} + 1) \times (\sqrt{2} - 1)} = \frac{\sqrt{2} - 1}{(\sqrt{2})^{2} - 1^{2}} = \frac{\sqrt{2} - 1}{2 - 1} = \sqrt{2} - 1$ ．
方法二： $\frac{1}{\sqrt{2} + 1} = \frac{2 - 1}{\sqrt{2} + 1} = \frac{(\sqrt{2} + 1) \times (\sqrt{2} - 1)}{\sqrt{2} + 1} = \sqrt{2} - 1$ ．

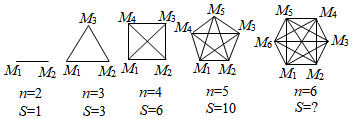
(1)、请分别参照以上两种方法化简： $\frac{1}{\sqrt{5} + 2}$ ；

(2)、计算 $(\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + ⋯ + \frac{1}{\sqrt{2022} + \sqrt{2021}}) (\sqrt{2022} + 1)$ ．

查看试题解析
18. 已知关于 $x$ 的一元二次方程 $m x^{2} - (m - 3) x - 3 = 0 (m \neq 0)$

(1)、求证：该方程一定有实数根；

(2)、若该方程有两个不相等的整数根，求整数 $m$ 的值．

查看试题解析
19. 【问题提出】在2020年抗击新冠肺炎的斗争中，某中学响应政府“停课不停学”的号召进行线上学习，七年级一班的全体同学在自主完成学习任务的同时，全班每两个同学都通过一次视频电话，彼此关怀，互相勉励，共同提高，若每两名同学之间仅通过一次视频电话，如何求全班50名同学共通过多少次电话呢？
【模型构建】用点M₁、M₂、M₃、…、M₅₀分别表示第1、2、3、…、50名同学，把该班级人数n与视频通话次数S之间的关系用如图模型表示：

(1)、【问题解决】
填写如图中第5个图中S的值为．

(2)、通过探索发现，通电话次数S与该班级人数n之间的关系式为，则当n＝50时，对应的S＝．

(3)、若该班全体女生相互之间共通话190次，求该班共有多少名女生？

(4)、【问题拓展】
若该班数学兴趣小组的同学，每两位同学之间互发一条微信问候，小明统计全组共发送微信110条，则该班数学兴趣小组的人数是人．

查看试题解析
20. 某服装专卖店在销售中发现，一款衬衫每件进价为70元，销售价为100元时，每天可售出20件，今年受“疫情”影响，为尽快减少库存，商店决定采取适当的降价措施，经市场调查发现，如果每件衬衫降价1元，那么平均可多售出2件．

(1)、每件衬衫降价多少元时，平均每天赢利750元？

(2)、要想平均每天赢利1000元，可能吗？请说明理由．

查看试题解析
21. 春季是传染病的高发期，某校为了调查学生对传染病预防知识的了解情况，从全校学生中随机抽取了部分学生进行相关知识的测试，并将测试成绩（x）分为五个等级：A（ $90 ⩽ x ⩽ 100$ ），B（ $80 ⩽ x < 90$ ），C（ $70 ⩽ x < 80$ ），D（ $60 ⩽ x < 70$ ），E（ $50 ⩽ x < 60$ ），整理后分别绘制成如图所示的频数直方图和扇形统计图（部分信息不完整）

(1)、求测试等级为C的学生人数，井补全频数直方图

(2)、求扇形统计图中等级为B所对应的扇形圆心角的度数：

(3)、若全校1200名学生都参加测试，请根据抽样测试的结果，估计该校测试不低于80分的学生有多少人？

查看试题解析
22. 如图，在四边形ABCD中，∠B+∠ADC＝180°，CE平分∠BCD交AB于点E，连结DE．

(1)、若∠A＝50°，∠B＝85°，求∠BEC的度数；

(2)、若∠A＝∠1，求证：∠CDE＝∠DCE．

查看试题解析
23. 如图，在平行四边形ABCD中，AB＝10，AD＝16，∠A＝60°，P是射线AD上一点，连接PB，沿PB将△APB折叠，得△A'PB．

(1)、如图1所示，当∠DPA'＝10°时，∠A'PB＝度；

(2)、如图2所示，当PA'⊥BC时，求线段PA的长度；

(3)、当点P为AD中点时，点F是边AB上不与点A，B重合的一个动点，将△APF沿PF折叠，得到△A'PF，连接BA'，求△BA'F周长的最小值．

查看试题解析

	队员1	队员2	队员3	队员4
平均数 $\overset{—}{x}$ （秒）	51	50	51	50
方差s²（秒²）	3.5	3.5	14.5	15.5