安徽省安庆市怀宁县2021-2022学年八年级下学期期末测试数学试卷

试卷更新日期：2023-05-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，与 $\sqrt{3}$ 是同类二次根式的是（）

A、 $\sqrt{6}$ B、 $\sqrt{9}$ C、 $\sqrt{12}$ D、 $\sqrt{18}$

查看试题解析
2. 下列四组数据中不能作为直角三角形的三边长是（）

A、 $3 ， 4 ， 5$ B、 $13 ， 14 ， 15$ C、 $1 ， \sqrt{3} ， 2$ D、 $8 ， 15 ， 17$

查看试题解析
3. 用配方法解一元二次方程 $x^{2} + 2 x - 2 = 0$ 时，原方程可变形为（）

A、 ${(x + 1)}^{2} = 2$ B、 ${(x - 1)}^{2} = 2$ C、 ${(x + 1)}^{2} = 3$ D、 ${(x - 1)}^{2} = 3$

查看试题解析
4. 某校举行“汉字听写比赛”，5个班级代表队的符合题意答题数如图．这5个符合题意答题数所组成的一组数据的中位数和众数分别是（）

A、10，15 B、13，15 C、13，20 D、15，15

查看试题解析
5. 如图所示，四边形ABCD中，Q是CD上的一定点，P是BC上的一动点，E、F分别是PA、PQ两边的中点；当点P在BC边上移动的过程中，线段EF的长度将（）．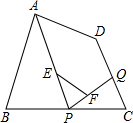

A、先变大，后变小 B、保持不变 C、先变小，后变大 D、无法确定

查看试题解析
6. 小玲的爸爸在钉制平行四边形框架时，采用了一种方法：如图所示，将两根木条AC，BD的中点重叠，并用钉子固定，则四边形ABCD就是平行四边形，这种方法的依据是（）

A、对角线互相平分的四边形是平行四边形 B、两组对角分别相等的四边形是平行四边形 C、两组对边分别相等的四边形是平行四边形 D、两组对边分别平行的四边形是平行四边形

查看试题解析
7. “赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若（a+b）²=21，大正方形的面积为13，则小正方形的面积为（）

A、3 B、4 C、5 D、6

查看试题解析
8. 方程 $x^{2} + 2 x - 3 = 0$ 的解为 $x_{1} = 1$ ， $x_{2} = - 3$ ，若方程 ${(2 x + 3)}^{2} + 2 (2 x + 3) - 3 = 0$ ，它的解是（）．

A、 $x_{1} = 1 ， x_{2} = 3$ B、 $x_{1} = 1 ， x_{2} = - 3$ C、 $x_{1} = - 1 ， x_{2} = 3$ D、 $x_{1} = - 1 ， x_{2} = - 3$

查看试题解析
9. 如图所示，数轴上点A所表示的数为a，则a的值是（）

A、-2+ $\sqrt{10}$ B、 $\sqrt{10}$ -1 C、-1- $\sqrt{10}$ D、2- $\sqrt{10}$

查看试题解析
10. 如图，在菱形ABCD中，对角线AC、BD相交于点O，延长CB至E使BE＝CD，连接AE，下列结论①AE＝2OD；②∠EAC＝90°；③四边形ADBE为菱形；④S_四_边_形AEBO＝ $\frac{3}{4}$ S_菱形ABCD中，正确的结论个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

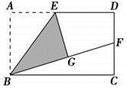
11. $\sqrt{27}$ 与最简二次根式 $\sqrt{m - 1}$ 是同类二次根式，则m= ．

查看试题解析
12. 平面直角坐标系中，点P(-4,2)到坐标原点的距离是

查看试题解析
13. 关于x的方程 $m x^{2} - 2 x + 5 = 0$ 有两个不相等的实数根，则m的取值范围是．

查看试题解析
14. 一个多边形的内角和是外角和的4倍，这个多边形的对角线有条．

查看试题解析
15. 如图，在矩形ABCD中，点E是AD的中点，将△ABE沿直线BE折叠后得到△GBE，延长BG交CD于点F，若AB=6，BC=4 $\sqrt{6}$ ，则FD=.

查看试题解析

三、解答题

16. 计算： $\sqrt{12} - \sqrt{\frac{9}{2}} +$ （ $\sqrt{5} - 2$ ）⁰ $+ \sqrt{(1 - \sqrt{2})^{2}}$ ．

查看试题解析
17. 观察以下等式：观察下列等式：
第1个等式： $\sqrt{\frac{1}{2} - \frac{1}{4}} = \frac{1}{2}$ ，

第2个等式： $\sqrt{\frac{1}{3} - \frac{1}{9}} = \frac{\sqrt{2}}{3}$ ，

第3个等式： $\sqrt{\frac{1}{4} - \frac{1}{16}} = \frac{\sqrt{3}}{4}$ ，

$\dots$

按照以上规律，解决下列问题：

(1)、写出第6个等式：；

(2)、写出你猜想的第n个等式：　　用含n的式子表示，并证明这个结论？

查看试题解析
18. 已知关于x的方程 $3 x^{2} + k x + k - 4 = 0$ ．

(1)、试说明无论k取何值时，方程总有两个不相等的实数根；

(2)、若k＝8，请解此方程．

查看试题解析
19. 在一条东西走向河的一侧有一村庄C，河边原有两个取水点A、B，其中AB＝BC，由于某种原因，由C到B的路现在已经不通，该村为方便村民取水决定在河边新建一个取水点D（A、D、B在同一条直线上），并新修一条路CD，测得CA＝750米，CD＝600米，AD＝450米．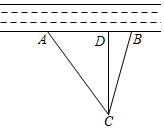

(1)、问CD是否为从村庄C到河边最近的路？请通过计算加以说明；

(2)、求原来的路线BC的长．

查看试题解析

20. 2022年4月16日，搭乘神舟十三号载人飞船的“航空三人组”顺利返回，为我国空间站建造再立新功．为了解我校九年级学生对我国空间站建设的关注程度，随机抽取了男、女学生若干名（抽取的男女生人数相同）进行问卷测试，问卷共30道选择题．现将得分情况统计，并绘制了如下不完整的统计图：（数据分组为A组：x＜18，B组：18≤x＜22，C组：22≤x＜26，D组：26≤x≤30，x表示问卷测试的分数）．其中男生得分处于C组的有14人．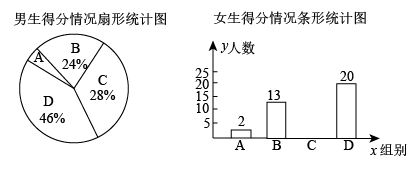

男生C组得分情况分别为：22，23，24，22，23，24，25，22，24，25，23，22，25，22；

抽取的男生、女生得分的平均数、中位数、众数（单位：分）如表所示：

组别	平均数	中位数	众数
男	20	a	22
女	20	23	20

(1)、随机抽取的男生人数为人，表格中a的值为，补全条形统计图；

(2)、通过以上数据分析，你认为是男生的成绩好还是女生的成绩好？说明理由（一条理由即可）

(3)、我校九年级学生中男、女生各900人，那么如果全体九年级学生参加此次问卷测试，估计成绩不低于26分的人数共有多少人？

查看试题解析

21. 在▱ABCD中，AB⊥AC，点O为AC的中点，点E、M分别为AB、CE上的点，连接MO并延长至点N，使MO＝NO．

(1)、判断四边形AMCN的形状，并加以证明；

(2)、当点M为CE中点时，请判断AC和MN之间的位置关系，并加以证明；

(3)、在（2）的条件下，若∠B＝60°，AB＝4，点E为AB中点，求四边形AMCN的面积．

查看试题解析
22. “蓝莓园里果盈枝，又到尝鲜采撷时”，今年我县蓝莓又喜获丰收．某水果商店从某蓝莓园购入一款进价为40元/千克的蓝莓，为了向消费者推广该蓝莓，商店计划开展为期10天的降价促销活动，调查发现，第1天的单价x（元/千克）和销量y（千克）均与t成一次函数关系，部分数据如下表．
t（天）
1
2
3
4
x（元/千克）
59
58
57
56
y（千克）
70
80
90
100

(1)、分别求x，y与t的函数表达式；

(2)、在活动开展的第几天，销售蓝莓的日利润为1650元；

(3)、请直接写出该活动进行到第几天时可以获得最大日利润，最大日利润为多少？

查看试题解析

t（天）	1	2	3	4
x（元/千克）	59	58	57	56
y（千克）	70	80	90	100