江苏省盐城市东台市第四联盟2022-2023学年七年级下学期期中数学试卷
试卷更新日期:2023-05-04 类型:期中考试
一、单选题
-
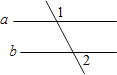
1. 下列现象是数学中的平移的是( )A、树叶从树上落下 B、电梯从底楼升到顶楼 C、骑自行车时轮胎的滚动 D、钟摆的摆动2. 有两根6cm、11cm的木棒,小明同学要想以这两根木棒做一个三角形,可以选用第三根木棒的长为( )A、3cm B、16cm C、20cm D、24cm3. 下列运算正确的是( )A、 B、 C、 D、4. 下列各式能用平方差公式计算的是( )A、 B、 C、 D、5. 如图,已知∠1=100°,若要使a∥b,则∠2=( )
 A、100° B、60° C、40° D、80°6. 每到四月,许多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其扰,据测定,杨絮纤维的直径约为0.000015m,该数值用科学记数法表示为( )A、1.5×105 B、0.15×10﹣4 C、1.5×10﹣5 D、15×10﹣77. 如图,在下列四组条件中,能判断的是( )
A、100° B、60° C、40° D、80°6. 每到四月,许多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其扰,据测定,杨絮纤维的直径约为0.000015m,该数值用科学记数法表示为( )A、1.5×105 B、0.15×10﹣4 C、1.5×10﹣5 D、15×10﹣77. 如图,在下列四组条件中,能判断的是( ) A、 B、 C、 D、8. 如图,将长方形沿线段折叠到的位置,若 , 则的度数为( )
A、 B、 C、 D、8. 如图,将长方形沿线段折叠到的位置,若 , 则的度数为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 计算: .10. 若多边形的每个内角都相等且内角和是540°,则该多边形的一个外角为 °.11. 若b-a=3,ab=1,则3a-3b(a+1)=.12. 等腰三角形的两边长分别是4和8 , 则它的周长是 .13. 已知 , 则.14. 如图,直线 , , , 则的度数是 度
 15. 沿某一方向行驶的汽车经过两次拐弯后与开始行驶的方向正好相反,若汽车第一次是右拐 , 则第二次应该是右拐 度16. 如图,把 纸片沿 折叠,当点C落在四边形 的外部时,此时测得 ,则 .
15. 沿某一方向行驶的汽车经过两次拐弯后与开始行驶的方向正好相反,若汽车第一次是右拐 , 则第二次应该是右拐 度16. 如图,把 纸片沿 折叠,当点C落在四边形 的外部时,此时测得 ,则 . 17. 为了求的值,可令 , 则 , 因此 , 所以 , 即 , 仿照以上方法计算的值是 .18. 古希腊的毕达哥拉斯学派对整数进行了深入的研究,尤其注意形与数的关系,“多边形数”也称为“形数”,就是形与数的结合物.用点排成的图形如下:其中:图①的点数叫做三角形数,从上至下第一个三角形数是1,第二个三角形数是 ,第三个三角形数是 ,……图②的点数叫做正方形数,从上至下第一个正方形数是1,第二个正方形数是 ,第三个正方形数是 ,……由此类推,图④中第五个正六边形数是.
17. 为了求的值,可令 , 则 , 因此 , 所以 , 即 , 仿照以上方法计算的值是 .18. 古希腊的毕达哥拉斯学派对整数进行了深入的研究,尤其注意形与数的关系,“多边形数”也称为“形数”,就是形与数的结合物.用点排成的图形如下:其中:图①的点数叫做三角形数,从上至下第一个三角形数是1,第二个三角形数是 ,第三个三角形数是 ,……图②的点数叫做正方形数,从上至下第一个正方形数是1,第二个正方形数是 ,第三个正方形数是 ,……由此类推,图④中第五个正六边形数是.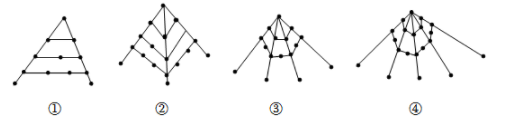
三、解答题
-
19. 计算:(1)、;(2)、;(3)、;(4)、.20. 如图,的顶点都在边长为的正方形方格纸的格点上,将向上平移格.

⑴请在图中画出平移后的三角形;
⑵在图中画出三角形的高、中线
21. 推理填空:如图,于 , 于 , , 可得平分.

理由如下:于 , 于 , (已知)
, (垂直的定义)
, ( )
▲ , ( )
, ( )
又 , (已知)
▲ , (等量代换)
平分(角平分线的定义)
22. 如图,AB∥CD,△EFG的顶点F,G分别落在直线AB,CD上,GE交AB于点H,GE平分∠FGD.若∠EFG=90°,∠E=35°,求∠EFB的度数.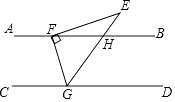 23. 如图,在四边形中, , .
23. 如图,在四边形中, , .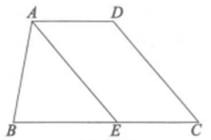 (1)、求的度数;(2)、平分交于点 , .求证:.24. 已知 , , 求:(1)、的值;(2)、的值;(3)、的值.25. 已知:点A在射线上,.
(1)、求的度数;(2)、平分交于点 , .求证:.24. 已知 , , 求:(1)、的值;(2)、的值;(3)、的值.25. 已知:点A在射线上,. (1)、如图 , 若 , 说明的理由;(2)、如图2,若 , 与交于点 , 请探究与的数量关系,写出你的探究结论,并说明理由.
(1)、如图 , 若 , 说明的理由;(2)、如图2,若 , 与交于点 , 请探究与的数量关系,写出你的探究结论,并说明理由.
