江苏省宿迁市泗阳县2022-2023学年七年级下学期期中数学试题
试卷更新日期:2023-05-04 类型:期中考试
一、单选题
-
1. 以下列各组线段的长为边,能组成三角形的是( )A、2、4、7 B、3、5、2 C、7、5、3 D、9、5、32. 如图,可以判定的条件是( )
 A、 B、 C、 D、3. 下列运算中,正确的是A、 B、 C、 D、4. 一个多边形的内角和是 , 则这个多边形的边数是( )A、10 B、11 C、9 D、85. 若二次三项式x2-mx+4是一个完全平方式,则字母m的值是 ( )A、±2 B、-2 C、±4 D、26. 若(x-5)(x+3)=x2+mx-15,则( )A、 B、 C、 D、7. 下列各式从左边到右边的变形是因式分解的是( )A、-18x4y3=-6x2y2·3x2y B、(a+2)(a-2)=a2-4 C、x2+2x+1=x(x+2)+1 D、a2-8a+16=(a-4)28. 如图,在中,点D、E分别在上,且 , , , 求的度数( )
A、 B、 C、 D、3. 下列运算中,正确的是A、 B、 C、 D、4. 一个多边形的内角和是 , 则这个多边形的边数是( )A、10 B、11 C、9 D、85. 若二次三项式x2-mx+4是一个完全平方式,则字母m的值是 ( )A、±2 B、-2 C、±4 D、26. 若(x-5)(x+3)=x2+mx-15,则( )A、 B、 C、 D、7. 下列各式从左边到右边的变形是因式分解的是( )A、-18x4y3=-6x2y2·3x2y B、(a+2)(a-2)=a2-4 C、x2+2x+1=x(x+2)+1 D、a2-8a+16=(a-4)28. 如图,在中,点D、E分别在上,且 , , , 求的度数( ) A、 B、 C、 D、9. 若 , , 则的值为( )A、10 B、16 C、18 D、3210. 将图甲中阴影部分的小长方形变换到图乙位置,能根据图形的面积关系得到的关系式是( )
A、 B、 C、 D、9. 若 , , 则的值为( )A、10 B、16 C、18 D、3210. 将图甲中阴影部分的小长方形变换到图乙位置,能根据图形的面积关系得到的关系式是( )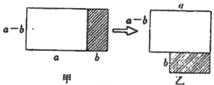 A、 B、 C、 D、11. 如图,直线AB∥CD,∠A=115°,∠E=80°,则∠CDE的度数为( )
A、 B、 C、 D、11. 如图,直线AB∥CD,∠A=115°,∠E=80°,则∠CDE的度数为( ) A、 B、 C、 D、12. 把下列各数代入中,等式成立的有( ),①;②;③;④;⑤.A、①②③ B、②③④ C、①②⑤ D、①④⑤
A、 B、 C、 D、12. 把下列各数代入中,等式成立的有( ),①;②;③;④;⑤.A、①②③ B、②③④ C、①②⑤ D、①④⑤二、填空题
-
13. 根据全国第七次人口普查数据显示,截至2020年11月1日零时,泗阳总人口约1063000人,数据1063000用科学记数法表示.14. 如图, , , 则.
 15. 已知 , 则代数式的值为.16. 如图,已知AE是△ABC的边BC上的中线,若AB=8cm,△ACE的周长比△AEB的周长多2cm,则AC=cm.
15. 已知 , 则代数式的值为.16. 如图,已知AE是△ABC的边BC上的中线,若AB=8cm,△ACE的周长比△AEB的周长多2cm,则AC=cm. 17. 如图所示:边长是a的正方形纸片的四个角各剪去一个边长为b的正方形,余下纸片的面积为.
17. 如图所示:边长是a的正方形纸片的四个角各剪去一个边长为b的正方形,余下纸片的面积为. 18. 如果 那么m的值为.19. 如图,中, , 将沿翻折后,点A落在边上的点处.如果 , 那么的度数为.
18. 如果 那么m的值为.19. 如图,中, , 将沿翻折后,点A落在边上的点处.如果 , 那么的度数为. 20. 由完全平方公式:可得 , 若 , 则的最大值为.
20. 由完全平方公式:可得 , 若 , 则的最大值为.三、解答题
-
21. 计算:(1)、(2)、.22. 因式分解:(1)、;(2)、.23. 先化简,再求值: , 其中.24. 如图, , , .
 (1)、求证:.(2)、探索与的数量关系,并说明理由.25. 如图所示:的角平分线相交于P, , 求的度数.
(1)、求证:.(2)、探索与的数量关系,并说明理由.25. 如图所示:的角平分线相交于P, , 求的度数. 26. 对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到 , 请解答下列问题:
26. 对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到 , 请解答下列问题: (1)、写出图2中所表示的数学等式.(2)、根据整式乘法的运算法则,通过计算验证上述等式.(3)、利用(1)中得到的结论,解决下面的问题:若 , , 则.27. 海伦是古希腊数学家,约公元62年左右活跃于亚历山大,年青时海伦酷爱数学,他的代表作《量度论》主要是研究面积、体积和几何分比问题,其中一段探究三角形面积的方法翻译如下:如图,设三角形面积为 , 以三角形各边为边向外作正方形,三个正方形的面积分别记作、、 , 定义:;;;; , 经研究发现,.如:三角形三条边分别为13、14、15,则 , , , , ;;; , 所以 , 故三角形的面积.
(1)、写出图2中所表示的数学等式.(2)、根据整式乘法的运算法则,通过计算验证上述等式.(3)、利用(1)中得到的结论,解决下面的问题:若 , , 则.27. 海伦是古希腊数学家,约公元62年左右活跃于亚历山大,年青时海伦酷爱数学,他的代表作《量度论》主要是研究面积、体积和几何分比问题,其中一段探究三角形面积的方法翻译如下:如图,设三角形面积为 , 以三角形各边为边向外作正方形,三个正方形的面积分别记作、、 , 定义:;;;; , 经研究发现,.如:三角形三条边分别为13、14、15,则 , , , , ;;; , 所以 , 故三角形的面积. (1)、若 , 则..(2)、当;;时.
(1)、若 , 则..(2)、当;;时.①求的表达式;
②若 , 求三角形的面积.
28. 如图1,将一只含角的直角三角板按如图摆放,其中 , 顶点A,C分别在直线上(),此时恰好平分 , 交直线于D点,过D点作交于E点,连接 , 在上取一点F,使 , 的角平分线交于G点.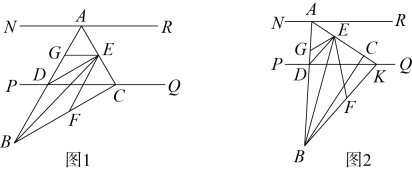 (1)、°;(2)、求证:平分;(3)、现将三角板绕顶点A逆时针旋转一定的度数(如图2),的延长线交于点K,连接 , 过D点作交于E点,在上取一点F,使得相等,的角平分线交于G点,若 , 求此时的度数.
(1)、°;(2)、求证:平分;(3)、现将三角板绕顶点A逆时针旋转一定的度数(如图2),的延长线交于点K,连接 , 过D点作交于E点,在上取一点F,使得相等,的角平分线交于G点,若 , 求此时的度数.