浙江省温州市平阳县2023年中考一模数学试题

试卷更新日期：2023-05-04 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算： $7 - (- 2)$ 的结果是（）

A、 $- 9$ B、 $- 5$ C、5 D、9

查看试题解析
2. 某物体如图所示，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 在2023年春节假期，全国国内旅游出游超过308000000人次.数据308000000用科学记数法表示为（）

A、 $308 \times 1 0^{6}$ B、 $30.8 \times 1 0^{7}$ C、 $3.08 \times 1 0^{8}$ D、 $0.308 \times 1 0^{9}$

查看试题解析
4. 解方程 $\frac{x + 2}{3} + \frac{2 x - 1}{4} = 1$ ，以下去分母正确的是（）

A、 $4 (x + 2) + 3 (2 x - 1) = 12$ B、 $4 (x + 2) + 3 (2 x - 1) = 1$ C、 $x + 2 + 2 x - 1 = 12$ D、 $3 (x + 2) + 4 (2 x - 1) = 12$

查看试题解析
5. 某日，甲、乙随机乘坐由平阳站开往雁荡山站的直达动车，具体车次如图.各车次各等级座位均有票，则两人乘坐同一趟车的概率是（）

A、 $\frac{1}{8}$ B、 $\frac{1}{4}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析

6. 在一次中考体育模拟测试中，某班41名学生参加测试（满分为40分），成绩统计如下表.部分数据被遮盖，下列统计量中，与被遮盖的数据无关的是（）

成绩（分）	32	34	36	37	38	39	40
人数（人）			2	6	19		7

A、中位数、众数 B、中位数、方差 C、平均数、众数 D、平均数、方差

查看试题解析

7. 如图， $A B$ 是 $⊙ O$ 的直径，点D是劣弧 $B C$ 上一点， $\overset{⌢}{B D} = \frac{1}{3} \overset{⌢}{B C}$ ，连结 $C D$ .若 $∠ A B C = 15 °$ ，则 $∠ D C O$ 的度数是（）

A、 $30 °$ B、 $35 °$ C、 $40 °$ D、 $50 °$

查看试题解析
8. 如图，小李身高 $A B = 1.6 m$ ，在路灯O的照射下，影子不全落在地面上.小李离路灯的距离 $A P = 6.6 m$ ，落在地面上影长 $A C = 0.9 m$ ，留在墙上的影高 $C D = 1 m$ ，则路灯 $O P$ 高为（）

A、5m B、6m C、7.5m D、8m

查看试题解析
9. 已知抛物线 $y = x^{2} - 2 m x - 3$ 经过点 $A (- 2 ， n)$ ，将点A先向右平移3个单位，再向下平移b个单位恰好落在抛物线的最低点处，则b的值为（）

A、3 B、4 C、5 D、9

查看试题解析
10. 如图，以正方形 $A B C D$ 的两边 $B C$ 和 $A D$ 为斜边向外作两个全等的直角三角形 $B C E$ 和 $D A F$ ，过点C作 $C G ⊥ A F$ 于点G，交 $A D$ 于点H，过点B作 $B I ⊥ C G$ 于点I，过点D作 $D K ⊥ B E$ ，交 $E B$ 延长线于点K，交 $C G$ 于点L.若 $S_{四边形 A B I G} = 2 S_{△ B C E}$ ， $G H = 1$ ，则 $D K$ 的长为（）

A、6 B、 $\frac{13}{2}$ C、7 D、 $\frac{15}{2}$

查看试题解析

二、填空题

11. 分解因式： $2 a^{2} - 4 a =$ .

查看试题解析
12. 某车站30位购票者等候购票时间的频数表如图所示，其中a的值为.
某车站30位购票者等候购票时间频数表
组别（分）
频数
频率
1
6
$0.2$
2
12
$0.4$
3
3
$0.1$
4
9
a

查看试题解析
13. 不等式组 ${\begin{array}{l} 1 - x > 0 \\ 3 x \geq 2 x - 4 \end{array}$ 的解为.

查看试题解析
14. 一个扇形的半径为6，弧长为3π，则此扇形的圆心角为度．

查看试题解析
15. 如图，点A，B，C在函数 $y = \frac{k}{x}$ （常数 $k > 0$ ， $x > 0$ ）图象上的位置如图所示，分别过点A，C作x轴与y轴的垂线，过点B作y轴与 $C D$ 的垂线.若 $O D ： D E ： E F = 2 ： 1 ： 3$ ，图中所构成的阴影部分面积为2，则矩形 $I G H C$ 的面积为.

查看试题解析
16. 图1是一种机械装置，当滑轮P绕固定点O旋转时，点P在 $A B$ 上滑动，带动点B绕固定点A旋转，使点C在水平杆 $M N$ 上来回滑动.图2是装置的侧面示意图， $A O ⊥ M N$ ， $O A = 10 c m$ ， $A B = 18 c m$ ， $B C = 12 c m$ ， $O P = 6 c m$ .当转动到 $O P^{'} ⊥ A B^{'}$ 时，点C滑到最左边 $C^{'}$ 处，此时A， $B^{'}$ ， $C^{'}$ 恰好在同一条直线上，则点O到 $M N$ 的距离是cm；当转动到 $O P^{″} ⊥ A B^{″}$ 时，点C滑到最右边 $C^{″}$ 处，则点 $C$ 在 $M N$ 上滑动的最大距离 $C^{'} C^{″} =$ cm.

查看试题解析

三、解答题

17.

(1)、计算： $| - 5 | - \sqrt{16} - {(1 + \sqrt{5})}^{0} + 2^{- 2}$ .

(2)、化简： ${(- x)}^{3} \cdot (- y) + {(- 2 x)}^{2} \cdot x y$ .

查看试题解析
18. 如图，在矩形 $A B C D$ 中，延长 $A D$ 至点E，使 $D E = A D$ ，连接 $B E$ 交 $D C$ 于点F.

(1)、求证： $△ D E F ≌ △ C B F$ .

(2)、若 $A B = 10$ ， $B C = 2$ ，求点A，F之间的距离.

查看试题解析

19. 学校组织“中国传统文化”知识竞赛，每班都有

20

名同学参加，成绩分为A，B，C，D四个等级，其中相应等级的得分依次记为

100

分，

90

分，

80

分，

70

分（

90

分及以上属于优秀），学校将七年一班和二班的成绩整理如下：

(1)、填写以下表格.

班级	平均数	众数	中位数	优秀率
七年一班	分	$90$ 分	分
七年二班	$92$ 分	分	90分	$80 ％$

(2)、结合以上统计量，你认为哪个班级的竞赛成绩更加优秀？请简述理由.

查看试题解析

20. 如图，在 $6 \times 6$ 的方格纸中， $△ A B C$ 的顶点均在格点上，请按要求画图.

(1)、在图中作一个以点A，B，C，D为顶点的格点四边形，且该四边形为中心对称图形.

(2)、在图中找一个格点E，连结 $B E$ ，使 $B E$ 将 $△ A B C$ 的面积分为 $2 ： 3$ .

查看试题解析
21. 已知抛物线 $y = x^{2} + 2 c x + c$ .

(1)、若抛物线与y轴的交点为 $(0 ， 3)$ ，求抛物线的函数表达式和顶点坐标.

(2)、已知抛物线与y轴的交点在y轴正半轴上，与x轴有交点.若点 $A (m ， n)$ ， $B (m - 4 ， n)$ 在抛物线上，求c的取值范围及m的最大值.

查看试题解析
22. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ B A C$ ，点G是 $A D$ 的中点，点F是 $A C$ 上一点， $A F = D F$ ，延长 $B G$ 交 $D F$ 的延长线于点E，连结 $A E$ .

(1)、证明：四边形 $A B D E$ 是平行四边形.

(2)、若 $A E = 6 \sqrt{5}$ ， $s i n ∠ A B C = \frac{2}{3}$ ，求 $C F$ 的长.

查看试题解析
23. 根据以下素材，设计落地窗的遮阳篷.
素材1：如图1，小浩家的窗户朝南，窗户的高度 $A B = 2 m$ ，此地一年中的正午时刻，太阳光与地平面的最小夹角为 $α$ ，最大夹角为 $β$ .如图2，小浩设计直角形遮阳篷 $B C D$ ，点C在 $A B$ 的延长线上， $C D ⊥ A C$ ，它既能最大限度地使冬天温暖的阳光射入室内（太阳光与 $B D$ 平行），又能最大限度地遮挡夏天炎热的阳光（太阳光与 $A D$ 平行）.
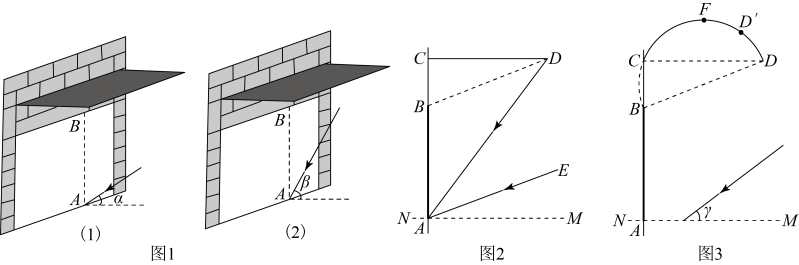
素材2：小浩查阅资料，计算出 $t a n α = \frac{1}{3}$ ， $t a n β = \frac{4}{3}$ （ $∠ E A M = α$ ， $∠ D A M = β$ ，如图2）.
素材3：如图3，为了美观及实用性，小浩再设计出圆弧形可伸缩遮阳篷（劣弧 $C D$ 延伸后经过点B， $D F$ 段可伸缩，F为 $\overset{⌢}{C D}$ 的中点）， $B C$ ， $C D$ 的长保持不变.

(1)、【任务1】如图2，求 $B C$ ， $C D$ 的长.

(2)、【任务2】如图3，求劣弧 $C D$ 的弓高.

(3)、【任务3】如图3，若某时太阳光与地平面的夹角r的正切值 $t a n γ = \frac{2}{3}$ ，要最大限度地使阳光射入室内，求遮阳篷点D上升高度的最小值（点 $D^{'}$ 到 $C D$ 的距离）.

查看试题解析
24. 如图，点O在 $R t △ A B C$ 的斜边 $A B$ 上，半圆O切 $A C$ 于点D，切 $B C$ 于点E，连结 $O D ， O E$ ， Q为线段 $B C$ 上一点， $Q P ⊥ A B$ 交 $A B$ 于点P，已知 $A C = 3$ ， $B C = 6$ ，设 $O P = x$ ， $E Q = y$ .

(1)、求半圆O的半径和 $O B$ 的长.

(2)、若点Q在线段 $B E$ 上.
①求y关于x的函数表达式.
②在 $O E$ 上取点F（不与点O重合），连结 $P F ， Q F$ ，当 $△ P Q F$ 为等腰直角三角形时，求所有满足条件x的值.

(3)、当 $P Q$ 经过 $\overset{⌢}{D E}$ 的中点G时，求 $Q G$ 的长.

查看试题解析

组别（分）	频数	频率
1	6	$0.2$
2	12	$0.4$
3	3	$0.1$
4	9	a