浙江省台州市路桥区2023年中考一模数学试题
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
1. 计算的结果是( ).A、6 B、5 C、 D、
-
2. 如图是由四个相同的小正方体组成的几何体,它的主视图是( ).
 A、
A、 B、
B、 C、
C、 D、
D、
-
3. 据国家电影局初步统计,2023年春节档(1月21日至1月27日)电影票房约为6758000000元,数据6758000000用科学记数法表示为( ).A、 B、 C、 D、
-
4. 下列运算正确的是( )A、 B、 C、 D、
-
5. 在某次数学测试中,10名学生的测试成绩(单位:分)统计如图所示,则这10名学生的测试成绩的众数是( ).
 A、87.5 B、90 C、95 D、92.5
A、87.5 B、90 C、95 D、92.5 -
6. 如图,将等腰三角形绕点C顺时针旋转得到 , 已知 , , 则的度数为( ).
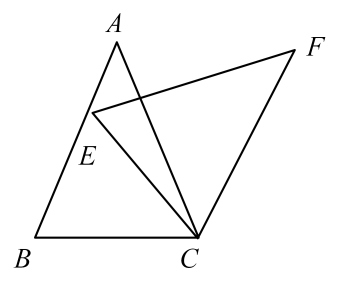 A、 B、 C、 D、
A、 B、 C、 D、 -
7. 如图,直线与x轴交点的横坐标为1,则关于x的方程的解为( ).
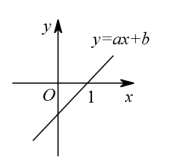 A、1 B、 C、2 D、
A、1 B、 C、2 D、 -
8. 观察下列尺规作图的痕迹,不能判断是等腰三角形的是( ).A、
 B、
B、 C、
C、 D、
D、
-
9. 如图是某品牌鞋服店推出的优惠活动,小明看中了一双鞋子和一双原价元的袜子,若购买这双鞋子和这双袜子所付的费用与单独购买这双鞋子所付的费用相同,则这双鞋子的原价可能是( ).



 A、元 B、元 C、元 D、元
A、元 B、元 C、元 D、元 -
10. 如图,不考虑空气阻力,以一定的速度将小球沿斜上方击出时,小球飞行的高度是飞行时间的二次函数.现以相同的初速度沿相同的方向每隔t秒依次击出三个质地一样的小球,小球在各自击出后1秒到达相同的最大飞行高度,若整个过程中同时出现在空中的小球个数最大值为2(不考虑小球落地后再弹起),则t的取值范围是( ).
 A、 B、 C、 D、
A、 B、 C、 D、
二、填空题
-
11. 分解因式: = .
-
12. 一个不透明的口袋中有四个质地相同的小球,把它们分别标号为1,2,3,4,随机摸取一个小球,其标号为偶数的概率是.
-
13. 已知点与点关于原点对称,则.
-
14. 如图,在中, , 将平移得到 , 当且经过边的中点D时,四边形的周长为.
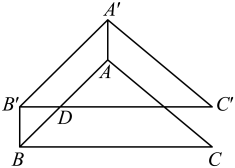
-
15. 定义一种新运算,当时,.若 , 则x=.
-
16. 如图,点O为等边三角形的中心,点D,E,F分别在边 , , 上,将 , , 分别沿着线段 , , 翻折,得到 , , , 且恰好都经过点O.与交于点G,与交于点H,与交于点I.
 (1)、若 , 则;(2)、设的面积为 , 的面积为 , 则.
(1)、若 , 则;(2)、设的面积为 , 的面积为 , 则.
三、解答题
-
17. 计算:.
-
18. 解不等式:.
-
19. 虎年岁末,台州进入轻轨时代,极大地方便了市民的出行,如图1是台州市城铁路线恩泽医院站出入口的自动扶梯,图2是其截面示意图,已知扶梯与购票厅地面的夹角 , 扶梯的长度为 , 求扶梯的底端C距离入口平台的高度.(结果精确到 , 参考数据: , , )

-
20. 某种气球内充满了一定质量的气体,当温度不变时,气球内气体的压强p(单位:)是气球的体积V(单位:)的反比例函数.现测得几组实验数据记录如下:
体积V(单位:)
…
…
压强p(单位:)
…
…
(1)、求p关于V的函数解析式;(2)、当气球内气体的压强大于时,气球将爆炸,为了安全起见,求气球的体积V的最小值. -
21. 如图,内接于半圆O,已知是半圆O的直径. , 平分 , 分别交半圆O和于点 , 过点D作 , 垂足为点H,交于点F.
 (1)、求证:;(2)、连接交于点G,若 , 求的长.
(1)、求证:;(2)、连接交于点G,若 , 求的长. -
22. 为了解同学们对垃圾分类知识的知晓程度,某校团委设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取若干名同学进行了问卷测试,根据测试成绩分布情况,整理得如下不完整的统计图表.
“垃圾分类知识及投放情况”问卷测试成绩统计表
组别
测试成绩/分
频数(人)
A
10
B
15
C
a
D
30
E
25
“垃圾分类知识及投放情况”问卷测试成绩的扇形统计图
 (1)、扇形统计图中B部分所对应的圆心角的度数为;(2)、本次测试成绩的中位数落在组;本次测试成绩的平均数是分;(3)、为了更好地宣传垃圾分类,在学校、家庭、社会的三位一体环境中发挥作用,学校团委决定组织在本次测试中达到一定分数的同学参加社区志愿活动,请你帮团委确定这个分数的标准,并用统计量说明其合理性.
(1)、扇形统计图中B部分所对应的圆心角的度数为;(2)、本次测试成绩的中位数落在组;本次测试成绩的平均数是分;(3)、为了更好地宣传垃圾分类,在学校、家庭、社会的三位一体环境中发挥作用,学校团委决定组织在本次测试中达到一定分数的同学参加社区志愿活动,请你帮团委确定这个分数的标准,并用统计量说明其合理性. -
23. 随着自动化设备的普及,公园中引入了自动喷灌系统.图1是某公园内的一个可垂直升降的草坪喷灌器,从喷水口喷出的水柱均为形状相同的抛物线,图2是该喷灌器喷水时的截面示意图.
 (1)、喷水口A离地高度为 , 喷出的水柱在离喷水口水平距离为处达到最高,高度为 , 且水柱刚好落在公园围栏和地面的交界B处.
(1)、喷水口A离地高度为 , 喷出的水柱在离喷水口水平距离为处达到最高,高度为 , 且水柱刚好落在公园围栏和地面的交界B处.①在图2中建立合适的平面直角坐标系,并求出抛物线的解析式;
②求喷灌器底端O到点B的距离;
(2)、现准备在公园内沿围栏建花坛,花坛的截面示意图为矩形(如图3),其中高为.宽为.为达到给花坛喷灌的效果,需将喷水口A向上升高 , 使水柱落在花坛的上方边上,求h的取值范围. -
24. 在中, , , D是边上的中点,E是直线右侧的一点,且 , 连接 , 过点D作的垂线交射线于点F.
 (1)、点C到的距离为;(2)、如图1,当点E在的外部时.
(1)、点C到的距离为;(2)、如图1,当点E在的外部时.①求证:;
②如图2,连接 , 当时,试探究与之间的数量关系;
(3)、若 , 请直接写出的长.
