浙江省台州市临海市2023年中考一模数学试题
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
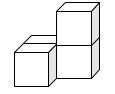
1. 如图是由四个相同的正方体搭成的立体图形,其主视图是( )
 A、
A、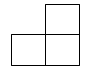 B、
B、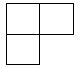 C、
C、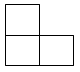 D、
D、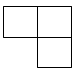 2. 我们可用数轴直观研究有理数及其运算.如图,将物体从点A向左平移5个单位到点B,可以描述这一变化过程的算式为( ).
2. 我们可用数轴直观研究有理数及其运算.如图,将物体从点A向左平移5个单位到点B,可以描述这一变化过程的算式为( ). A、 B、 C、 D、3. 无理数的大小在( ).A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间4. 正n边形的一个外角为30°,则n的值为( ).A、6 B、8 C、10 D、125. 下列运算正确的是( ).A、 B、 C、 D、6. 如图是路政工程车的工作示意图,工作篮底部与支撑平台平行.若 , , 则的度数为( ).
A、 B、 C、 D、3. 无理数的大小在( ).A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间4. 正n边形的一个外角为30°,则n的值为( ).A、6 B、8 C、10 D、125. 下列运算正确的是( ).A、 B、 C、 D、6. 如图是路政工程车的工作示意图,工作篮底部与支撑平台平行.若 , , 则的度数为( ).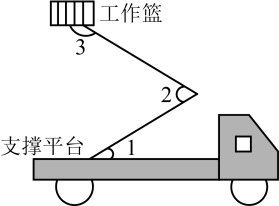 A、 B、 C、 D、7. 初三(9)班拍合照时,最后一排10位同学的身高(单位:)分别为 , 当他们站到一排高度相等的桌子上,头顶离地高度(单位:)分别为.对比两组数据,下列统计量中不发生变化的是( ).A、平均数 B、中位数 C、众数 D、方差8. 用破损量角器按如图方式测量∠ABC的度数,让∠ABC的顶点恰好在量角器圆弧上,两边分别经过圆弧上的A,C两点.若点A,C对应的刻度分别为55°,135°,则∠ABC的度数为( ).
A、 B、 C、 D、7. 初三(9)班拍合照时,最后一排10位同学的身高(单位:)分别为 , 当他们站到一排高度相等的桌子上,头顶离地高度(单位:)分别为.对比两组数据,下列统计量中不发生变化的是( ).A、平均数 B、中位数 C、众数 D、方差8. 用破损量角器按如图方式测量∠ABC的度数,让∠ABC的顶点恰好在量角器圆弧上,两边分别经过圆弧上的A,C两点.若点A,C对应的刻度分别为55°,135°,则∠ABC的度数为( ). A、130° B、135° C、140° D、145°9. 如图,在正方形中,点E,F分别在边 , 上,且 , 作于点H,交于点G.若 , , 则的长为( ).
A、130° B、135° C、140° D、145°9. 如图,在正方形中,点E,F分别在边 , 上,且 , 作于点H,交于点G.若 , , 则的长为( ). A、4 B、3 C、2 D、110. 若反比例函数的图象经过点 , 则k的取值范围为( ).A、 B、 C、 D、
A、4 B、3 C、2 D、110. 若反比例函数的图象经过点 , 则k的取值范围为( ).A、 B、 C、 D、二、填空题
-
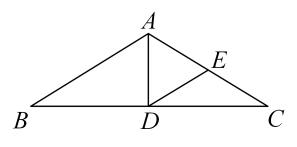
11. 因式分解:.12. 将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)掷一次,朝上一面点数是1的概率为 .13. 如图,中, , 平分 , 点E为中点,则的长为.
 14. 关于某个四边形的三个特征描述:①对角线互相垂直;②对角线互相平分;③一组邻边相等. 选择其中两个作为条件,另一个作为结论. 若该命题是假命题,则选择的条件是.(填序号)15. 公元前6世纪,古希腊学者泰勒斯用图1的方法巧测金字塔的高度.如图2,小明仿照这个方法,测量圆锥形小山包的高度,已知圆锥底面周长为62.8 m. 先在小山包旁边立起一根木棒,当木棒影子长度等于木棒高度时,测得小山包影子AB长为23 m(直线AB过底面圆心),则小山包的高为m(π取3.14).
14. 关于某个四边形的三个特征描述:①对角线互相垂直;②对角线互相平分;③一组邻边相等. 选择其中两个作为条件,另一个作为结论. 若该命题是假命题,则选择的条件是.(填序号)15. 公元前6世纪,古希腊学者泰勒斯用图1的方法巧测金字塔的高度.如图2,小明仿照这个方法,测量圆锥形小山包的高度,已知圆锥底面周长为62.8 m. 先在小山包旁边立起一根木棒,当木棒影子长度等于木棒高度时,测得小山包影子AB长为23 m(直线AB过底面圆心),则小山包的高为m(π取3.14).
 16. 若二次函数的图象经过点 , , , 且 , 则下列结论:
16. 若二次函数的图象经过点 , , , 且 , 则下列结论:①;②;③;④中,一定成立的有.(填序号)
三、解答题
-
17. 计算:.18. 小红解答下题“先化简,再求值: , 其中”的过程如下:
解:原式 , 当时,原式.
小红的解答正确吗?如果不正确,请写出正确的答案.
19. 小波某时刻想喝水,饮水机显示水温为30 ℃,为预测水烧开的时间,小波每隔1分钟观察一次水温,得到数据如表.等待时间t/分钟
0
1
2
3
水温T/℃
30
40
50
60
(1)、求水温T(单位:℃)关于等待时间t(单位:分钟)的函数解析式.(2)、求小波喝到100 ℃开水的最短等待时间.20. 图1是一款笔记本电脑支架,它便于电脑散热,减轻使用者的颈椎压力.图2是支架与电脑底部的接触面以及侧面的抽象图.已知 , 互相平分于点O, , 若 , . (1)、求的长.(2)、求点D到底架的高.(结果精确到;参考数据: , , )21. 共15名应聘者到广告公司竞聘设计师,考核分笔试、面试两个阶段,考核成绩均采用10分制.笔试成绩前8名进入面试. 分别赋予笔试、面试成绩一定的权重,得到综合成绩,择优录取. 15名应聘者的笔试成绩如下表,其中应聘者小金知道自己的笔试成绩为7分.
(1)、求的长.(2)、求点D到底架的高.(结果精确到;参考数据: , , )21. 共15名应聘者到广告公司竞聘设计师,考核分笔试、面试两个阶段,考核成绩均采用10分制.笔试成绩前8名进入面试. 分别赋予笔试、面试成绩一定的权重,得到综合成绩,择优录取. 15名应聘者的笔试成绩如下表,其中应聘者小金知道自己的笔试成绩为7分.笔试成绩/分
2
3
4
5
6
7
8
9
频数
1
1
1
4
2
3
2
1
(1)、①求15名应聘者的笔试平均成绩;②小金想确定能否进入面试,应关注15名应聘者笔试成绩的平均数、中位数中的哪一个?
(2)、小金最后的综合成绩仅为3.4分,请作出合理分析.22. 如图,C为线段AB上一点, , , 射线于点C,P为射线CD上一点,连接PA,PB.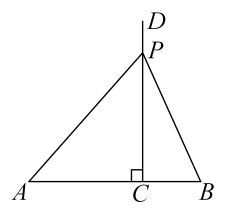 (1)、【发现、提出问题】
(1)、【发现、提出问题】①当时,求的值;
②小亮发现PC取不同值时,的值存在一定规律,请猜想该规律.
(2)、【分析、解决问题】请证明你的猜想.(3)、【运用】当时,的周长为.23. 如图1,点光源O射出光线沿直线传播,将胶片上的建筑物图片投影到与胶片平行的屏幕上,形成影像.已知 , 胶片与屏幕的距离为定值,设点光源到胶片的距离长为x(单位:),CD长为y(单位:),当时,. (1)、求的长.(2)、求y关于x的函数解析式,在图中画出图像,并写出至少一条该函数性质.(3)、若要求不小于 , 求的取值范围.24. 如图,正方形的边长为 , 点E在上,.正方形内存在匀强磁场,某种带电粒子以速度v(单位:)沿着EF方向从点E射入匀强磁场,在磁场中沿逆时针方向作匀速圆周运动,该圆与相切,半径r(单位:m)与v满足关系(k为常数).如图1,当时,粒子恰好从点A处射出磁场.
(1)、求的长.(2)、求y关于x的函数解析式,在图中画出图像,并写出至少一条该函数性质.(3)、若要求不小于 , 求的取值范围.24. 如图,正方形的边长为 , 点E在上,.正方形内存在匀强磁场,某种带电粒子以速度v(单位:)沿着EF方向从点E射入匀强磁场,在磁场中沿逆时针方向作匀速圆周运动,该圆与相切,半径r(单位:m)与v满足关系(k为常数).如图1,当时,粒子恰好从点A处射出磁场. (1)、①求常数k的值;
(1)、①求常数k的值;②若或6,粒子在磁场中的运动时间分别为 , , 请比较 , 的大小.
(2)、如图2,若粒子从边上一点G射出磁场,请用无刻度的直尺和圆规画出粒子运动的弧形路径的圆心О(保留作图痕迹).(3)、该种粒子能否从边上射出磁场﹖若能,请求出v的取值范围;若不能,请写出理由.