浙江省丽水市缙云县2023年中考一模数学试题
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、20232. 如图是由五个相同的正方体搭成的立体图形,其主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下面四个数中与 最接近的数是( )A、2 B、3 C、4 D、54. 如图是一款教室护眼灯 , 用两根电线 , 吊在天花板上,已知 , 为保证护眼灯与天花板平行,添加下列条件中,正确的是( )
3. 下面四个数中与 最接近的数是( )A、2 B、3 C、4 D、54. 如图是一款教室护眼灯 , 用两根电线 , 吊在天花板上,已知 , 为保证护眼灯与天花板平行,添加下列条件中,正确的是( )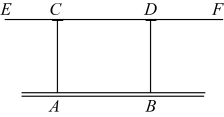 A、 B、 C、 D、5. 计算的结果是( )A、 B、 C、 D、6. 在一个不透明的袋中有6个只有颜色不同的球,其中4个黑球和2个白球.从袋中任意摸出一个球,是黑球的概率为( )A、 B、 C、 D、7. 四盏灯笼的位置如图,已知A,B,C,D的坐标分别是 , , , , 平移其中一盏灯,使得y轴两边的灯笼对称,下列说法正确的是( )
A、 B、 C、 D、5. 计算的结果是( )A、 B、 C、 D、6. 在一个不透明的袋中有6个只有颜色不同的球,其中4个黑球和2个白球.从袋中任意摸出一个球,是黑球的概率为( )A、 B、 C、 D、7. 四盏灯笼的位置如图,已知A,B,C,D的坐标分别是 , , , , 平移其中一盏灯,使得y轴两边的灯笼对称,下列说法正确的是( ) A、平移点A到 B、平移点B到 C、平移点C到 D、平移点C到8. 若A种糖的单价为元/千克,B种糖的单价为元/千克,则m千克A种糖和n千克B种糖混合而成的什锦糖的单价为( )A、元/千克 B、元/千克 C、元/千克 D、元/千克9. 将一圆柱体从水中匀速提起,从如图所示开始计时,直至其下表面刚好离开水面,停止计时.用x表示圆柱体运动时间,y表示水面的高度,则y与x之间函数关系的图象大致是( )
A、平移点A到 B、平移点B到 C、平移点C到 D、平移点C到8. 若A种糖的单价为元/千克,B种糖的单价为元/千克,则m千克A种糖和n千克B种糖混合而成的什锦糖的单价为( )A、元/千克 B、元/千克 C、元/千克 D、元/千克9. 将一圆柱体从水中匀速提起,从如图所示开始计时,直至其下表面刚好离开水面,停止计时.用x表示圆柱体运动时间,y表示水面的高度,则y与x之间函数关系的图象大致是( )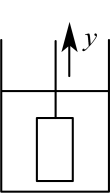 A、
A、 B、
B、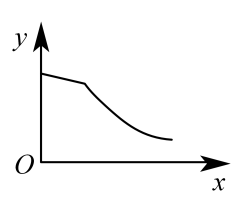 C、
C、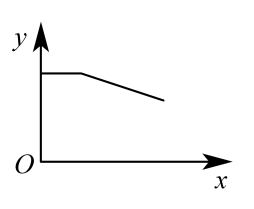 D、
D、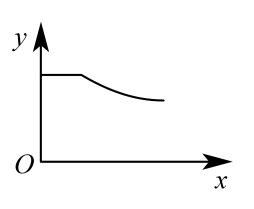 10. 小明同学为班级设计如图所示的班徽,O为正方形的中心,四块全等的阴影图形均为菱形.若A,E,F三点共线,则图中阴影面积与空白面积之比为( )
10. 小明同学为班级设计如图所示的班徽,O为正方形的中心,四块全等的阴影图形均为菱形.若A,E,F三点共线,则图中阴影面积与空白面积之比为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
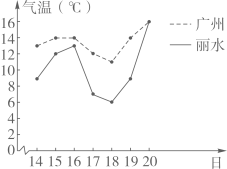
11. 分解因式: .12. 丽水和广州两个城市在2022年12月14日~20日的气温(当日最高气温)折线统计图如图所示,丽水和广州的气温方差分别为与 , 则(填“>”、“=”、“<”中的一个).
 13. 已知关于x的方程有两个不相等的实数根,则k的取值范围是 .14. 如图,为的对角线, , 点E在上,连接 , 分别延长 , 交于点F,若 , 则的长为
13. 已知关于x的方程有两个不相等的实数根,则k的取值范围是 .14. 如图,为的对角线, , 点E在上,连接 , 分别延长 , 交于点F,若 , 则的长为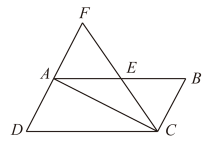 15. 蛋形九巧板源于1983年上市的“哥伦布蛋形拼图”(如图1),是七巧板的变形和延伸.如图2, , 是两条互相垂直的直径,分别以点A,B为圆心,的长为半径画圆弧,交 , 的延长线于点E,F,再以点C为圆心,的长为半径画 , 形成蛋形九巧板轮廓.若 , 则蛋形九巧板外围周长为.
15. 蛋形九巧板源于1983年上市的“哥伦布蛋形拼图”(如图1),是七巧板的变形和延伸.如图2, , 是两条互相垂直的直径,分别以点A,B为圆心,的长为半径画圆弧,交 , 的延长线于点E,F,再以点C为圆心,的长为半径画 , 形成蛋形九巧板轮廓.若 , 则蛋形九巧板外围周长为. 16. 如图,在矩形中, , .折叠该矩形,使点D落在边上的点G处,折痕分别与边 , 交于点E,F.取的中点H,连接 , 沿折叠,使点C恰好落在上的点I处,则GI的长为.
16. 如图,在矩形中, , .折叠该矩形,使点D落在边上的点G处,折痕分别与边 , 交于点E,F.取的中点H,连接 , 沿折叠,使点C恰好落在上的点I处,则GI的长为.
三、解答题
-
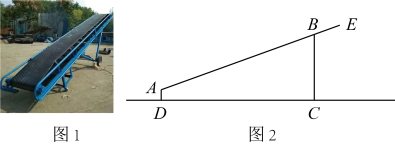
17. 计算:.18. 解方程组:19. 如图1,是一台小型输送机,其示意图如图2所示.已知两个支架的端点的距离 , 传输带与支架所成的角 , 支架端点A离地面的高度 , 求支架端点B离地面的高度.(结果精确到0.1m;参考数据 , , ).
 20. 如图,取一根长的均匀木杆,用细绳绑在木杆的中点O并将其吊起来.在中点O的左侧挂一个物体,在中点O的右侧用一个弹簧秤向下拉,使木杆处于水平状态.根据杠杆原理,当物体保持不动时,弹簧秤的示数y(单位:N)是x(弹簧秤与中点O的距离)(单位:)的反比例函数,当时,.
20. 如图,取一根长的均匀木杆,用细绳绑在木杆的中点O并将其吊起来.在中点O的左侧挂一个物体,在中点O的右侧用一个弹簧秤向下拉,使木杆处于水平状态.根据杠杆原理,当物体保持不动时,弹簧秤的示数y(单位:N)是x(弹簧秤与中点O的距离)(单位:)的反比例函数,当时,. (1)、求y关于x的函数表达式.(2)、移动弹簧秤的位置,若木杆仍处于水平状态,求弹簧秤的示数的最小值.21. 如图,中,于D,于E,与相交于点F,.
(1)、求y关于x的函数表达式.(2)、移动弹簧秤的位置,若木杆仍处于水平状态,求弹簧秤的示数的最小值.21. 如图,中,于D,于E,与相交于点F,. (1)、求证:;(2)、若 , 求的度数.22. 小明调查了世界杯和世界杯每个参赛国的进球数,设每个参赛国的进球数为T个.按照进球数分成五组:A组“”,B组“”,C组“”,D组“”,组“”.将收集的数据整理后,绘制成如下两幅统计图表.
(1)、求证:;(2)、若 , 求的度数.22. 小明调查了世界杯和世界杯每个参赛国的进球数,设每个参赛国的进球数为T个.按照进球数分成五组:A组“”,B组“”,C组“”,D组“”,组“”.将收集的数据整理后,绘制成如下两幅统计图表.
世界杯每个参赛国进球数统计表
组别
国家数
A
12
B
12
C
4
D
3
E
1
(1)、世界杯每个参赛国进球数的中位数落在哪一组?(2)、根据组中值分别求世界杯和世界杯每个参赛国进球的平均数.(3)、请选择适合的统计量,从多角度对世界杯与世界杯的进球数进行分析,踢球技术是进步了还是退步了?23. 如图,为矩形的对角线,点E在上,连接 , F是的外接圆与的延长线的一个交点,延长交圆于点G,点D恰好是的中点,连接 , 分别交 , 于点H,M,连接. (1)、求证:.(2)、求证:四边形是菱形.(3)、若H恰好是的中点时,求的值.24. 某天,小明在足球场上练习“落叶球”(如图1),足球运动轨迹是抛物线的一部分,如图2,足球起点在A处,正对一门柱 , 距离 , 足球运动到B的正上方,到达最高点2.5m,此时.球门宽 , 高.
(1)、求证:.(2)、求证:四边形是菱形.(3)、若H恰好是的中点时,求的值.24. 某天,小明在足球场上练习“落叶球”(如图1),足球运动轨迹是抛物线的一部分,如图2,足球起点在A处,正对一门柱 , 距离 , 足球运动到B的正上方,到达最高点2.5m,此时.球门宽 , 高. (1)、以水平方向为x轴,A为原点建立坐标系,求足球运动轨迹抛物线的函数表达式.(2)、请判断足球能否进球网?并说明理由.(3)、小明改变踢球方向,踢球时,保持足球运动轨迹抛物线形状不变的前提下,足球恰好在点E处进入球网.若离A点8m处有人墙 , 且 , 人起跳后最大高度为2.2m,请探求此时足球能否越过人墙,并说明理由.
(1)、以水平方向为x轴,A为原点建立坐标系,求足球运动轨迹抛物线的函数表达式.(2)、请判断足球能否进球网?并说明理由.(3)、小明改变踢球方向,踢球时,保持足球运动轨迹抛物线形状不变的前提下,足球恰好在点E处进入球网.若离A点8m处有人墙 , 且 , 人起跳后最大高度为2.2m,请探求此时足球能否越过人墙,并说明理由.