江苏省盐城市建湖县2023年中考一模数学试题

试卷更新日期：2023-05-04 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列数中，最小的是（）

A、 $- 1$ B、 $| - 2023 |$ C、0 D、2

查看试题解析
2. 下列计算结果正确的是（）

A、 $3 x^{4} + 2 x^{2} = 5 x^{6}$ B、 $x^{8} \div x^{4} = x^{2}$ C、 ${(- 2 x^{3})}^{3} = - 6 x^{9}$ D、 $3 x^{3} \cdot 2 x = 6 x^{4}$

查看试题解析
3. 国家统计局发布2022年国民总收入 $1197000$ 亿元，比上年增长 $2.8 %$ ，将 $1197000$ 用科学记数法表示应为（）

A、 $1197 \times 1 0^{3}$ B、 $11.97 \times 1 0^{5}$ C、 $1.197 \times 1 0^{6}$ D、 $1.197 \times 1 0^{5}$

查看试题解析
4. 如图，将一块直角三角板的直角顶点放在直尺的一边上.若 $∠ 2 = 65 °$ ，则 $∠ 1$ 的度数是（）

A、 $35 °$ B、 $25 °$ C、 $65 °$ D、 $55 °$

查看试题解析
5. 已知二元一次方程 $2 x + 3 y = 3$ ，其中x与y互为相反数，则x、y的值为（）

A、 ${\begin{array}{l} x = - 4 \\ y = 4 \end{array}$ B、 ${\begin{array}{l} x = 4 \\ y = - 4 \end{array}$ C、 ${\begin{array}{l} x = 3 \\ y = - 3 \end{array}$ D、 ${\begin{array}{l} x = - 3 \\ y = 3 \end{array}$

查看试题解析
6. 如图，在 $△ A B C$ 中， $B C$ 的垂直平分线分别交 $A C$ 、 $B C$ 于点D、E.若 $△ A B C$ 的周长为24， $C E = 5$ ，则 $△ A B D$ 的周长为（）

A、12 B、14 C、16 D、18

查看试题解析
7. 如图，直线 $E F$ 经过 $▱ A B C D$ 的对角线交点O，若平行四边形 $A B C D$ 的面积为 $36 c m^{2}$ ，则四边形 $E D C F$ 的面积为（）

A、 $12 c m^{2}$ B、 $18 c m^{2}$ C、 $24 c m^{2}$ D、 $27 c m^{2}$

查看试题解析
8. 用绘图软件绘制出函数 $y = \frac{a x}{{(x + b)}^{2}}$ 的图象，如图，则根据你学习函数图象的经验，下列对a、b大小的判断，正确的是（）

A、 $a > 0$ ， $b < 0$ B、 $a > 0$ ， $b > 0$ C、 $a < 0$ ， $b > 0$ D、 $a < 0$ ， $b < 0$

查看试题解析

二、填空题

9. 若分式 $\frac{3 x}{x + 2}$ 有意义，则x的取值范围为.

查看试题解析
10. 因式分解：a³ $-$ 16ab²=

查看试题解析
11. 某超市销售A，B，C，D四种矿泉水，它们的单价依次是5元、3元、2元、1元，某天的销售情况如图所示，则这天销售的矿泉水的平均单价是元.

查看试题解析
12. 关于x的分式方程 $\frac{1}{x - 1} + \frac{a - 1}{1 - x} = 2$ 的解为正数，则a的取值范围是 .

查看试题解析
13. 如图，点A、B、C、D、E在同一平面内，连接 $A B 、 B C 、 C D 、 D E 、 E A$ ，若 $∠ A B C = 125 °$ ，则 $∠ A + ∠ C + ∠ D + ∠ E =$ $°$ .

查看试题解析
14. 如图，点A、B、C都在 $⊙ O$ 上，如果 $∠ A O C = ∠ A B C$ ，那么 $∠ A B C$ 的度数为 $°$ .

查看试题解析
15. 如图，在平面直角坐标系中，四边形 $A B C D$ 为正方形，点A的坐标为 $(0 ， 3)$ ，点B的坐标为 $(5 ， 0)$ ，点E为对角线的交点，则点E的坐标为.

查看试题解析
16. 如图，矩形 $A B C D$ 中， $A B = 4$ ， $A D = 8$ ，点E在边 $A D$ 上，且 $A E ： E D = 1 ： 3$ ，动点P从点A出发，沿 $A B$ 运动到点B停止，过点E作 $E P ⊥ Q E$ 交射线 $B C$ 于点Q，设O是线段 $E Q$ 的中点，则在点P运动的整个过程中，点O运动路线的长为.

查看试题解析

三、解答题

17. 计算： ${(- 2023 + π)}^{0} - \sqrt{2} c o s 45 ° + {(- \frac{1}{2})}^{- 2}$ .

查看试题解析
18. 解不等式组 ${\begin{array}{l} 4 (x - 1) < 3 x - 2 ① \\ \frac{x + 3}{3} - 1 \leq \frac{x + 2}{2} ② \end{array}$ ，并将其解集在数轴上表示出来.

查看试题解析
19. 先化简，再求值： $(1 - \frac{4}{m + 1}) \div \frac{m^{2} - 6 m + 9}{3 m + 3}$ ，再从-1、0、1、3中选择一个适合的m的值代入求值.

查看试题解析
20. 如图，在 $▱ A B C D$ 中， $A C ， B D$ 交于点 $O$ ，点 $E ， F$ 在 $A C$ 上， $A E = C F$ ．

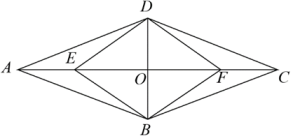(1)、求证：四边形 $E B F D$ 是平行四边形；

(2)、若 $∠ B A C = ∠ D A C ，$ 求证：四边形 $E B F D$ 是菱形．

查看试题解析
21. “双减”政策下，将课后服务作为学生核心素养培养的重要阵地，聚力打造高品质和高成效的服务课程，推动提升课后服务质量，助力学生全面健康成长.某校确立了A：科技：B：运动；C：艺术；D：项目化研究四大课程领域（每人限报一个）.若该校小陆和小明两名同学各随机选择一个课程领域.

(1)、小陆选择项目化研究课程领域的概率是；

(2)、用画树状图或列表的方法，求小陆和小明选择同一个课程领域的概率.

查看试题解析
22. 今年的4月15日是第八个全民国家安全教育日，某校为了解学生的安全意识，在全校范围内随机抽取部分学生进行问卷调查.根据调查结果，把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次类别，并绘制如下两幅尚不完整的统计图.

根据以上信息，解答下列问题：

(1)、这次调查一共抽取了名学生，请将条形统计图补充完整；

(2)、扇形统计图中，“较强”层次类别所占圆心角的为°；

(3)、若该校有1800名学生，现要对安全意识为“淡薄”、“一般”的学生强化安全教育，请根据以上调查结果估算，全校需要强化安全教育的学生共有多少名？

查看试题解析
23. 如图，在 $△ A B C$ 中， $A B = A C$ ，点D在 $A C$ 边上（不与点A，点C重合），连接 $B D$ ， $B D = A B$ .

(1)、设 $∠ C B D = 30 °$ 时，求 $∠ A B D$ 的度数；

(2)、若 $A B = 10$ ， $B C = 12$ ，求 $A D$ 的长.

查看试题解析
24. 为创建和谐文明的校园环境，某初中准备购买A、B两种分类垃圾桶，通过市场调研得知：A种垃圾桶每组的单价比B种垃圾桶每组的单价少 $50$ 元，且用 $8000$ 元购买A种垃圾桶的组数量与用 $10000$ 元购买B种垃圾桶的组数量相同.

(1)、求A、B两种垃圾桶每组的单价分别是多少元；

(2)、该学校计划用不超过 $6850$ 元的资金购买A、B两种垃圾桶共 $30$ 组，则最多可以购买B种垃圾桶多少组？

查看试题解析
25. 如图， $⊙ O$ 的半径是 $2 \sqrt{5}$ ， AB是 $⊙ O$ 的直径，半径 $O C ⊥ A B$ 于点O，点E是半径 $O A$ 上一点， $C E$ 交 $⊙ O$ 于点D，且 $P D = P E$ .

(1)、求证： $P D$ 是 $⊙ O$ 的切线；

(2)、若 $t a n ∠ A C D = \frac{1}{2}$ ，求： $B D$ 和 $A C$ 的长.

查看试题解析
26.

(1)、【问题思考】
如图1，点E是正方形 $A B C D$ 内的一点，过点E的直线 $A Q$ ，以 $D E$ 为边向右侧作正方形 $D E F G$ ，连接 $G C$ ，直线 $G C$ 与直线 $A Q$ 交于点P，则线段 $A E$ 与 $G C$ 之间的关系为.

(2)、【问题类比】
如图2，当点E是正方形 $A B C D$ 外的一点时，【问题思考】中的结论还成立吗？若成立，请证明你的结论；若不成立，请说明理由；

(3)、【拓展延伸】
如图3，点E是边长为6的正方形 $A B C D$ 所在平面内一动点，【问题思考】中其他条件不变，则动点P到边 $A D$ 的最大距离为（直接写出结果）.

查看试题解析
27. 如图1，抛物线 $y_{1} = a x^{2} - 3 x + c$ 的图象与x轴的交点为A和B，与y轴交点为 $D (0 ， 4)$ ，与直线 $y_{2} = - x + b$ 交点为A和C，且 $O A = O D$ .

(1)、求抛物线的解析式和b值；

(2)、在直线 $y_{2} = - x + b$ 上是否存在一点P，使得 $△ A B P$ 是等腰直角三角形，如果存在，求出点P的坐标，如果不存在，请说明理由；

(3)、将抛物线 $y_{1}$ 图象x轴上方的部分沿x轴翻折得一个“M”形状的新图象（如图2），若直线 $y_{3} = - x + n$ 与该新图象恰好有四个公共点，请求出此时n的取值范围.

查看试题解析