湖南省株洲市石峰区2023年九年级数学素养监测卷(一)
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、2 C、 D、2. 在实数 , 0, , 中,最小的是( )A、 B、0 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 在平面直角坐标系中,点在( )A、x轴上 B、y轴上 C、第三象限 D、第四象限5. 某校规定学生的数学综合成绩满分为100分,其中期中成绩占40%,期末成绩占60%,小明的期中和期末考试成绩分别是90分,95分,则小明的综合成绩是( )A、92分 B、93分 C、94分 D、95分6. 下列关于矩形的说法正确的是( )A、对角线垂直 B、四个角都是直角 C、有四条对称轴 D、四条边相等7. 方程的解为( )A、 B、 C、 D、8. 不等式的解集在数轴上表示正确的是( )A、
 B、
B、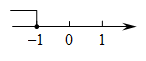 C、
C、 D、
D、 9. 如图,等腰内接于 , 点D是圆中优孤上一点,连接 , 已知 , 则的度数为( )
9. 如图,等腰内接于 , 点D是圆中优孤上一点,连接 , 已知 , 则的度数为( )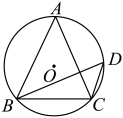 A、 B、 C、 D、10. 已知二次函数和一次函数 , 则这两个函数在同一个平面直角坐标系中的大致图象是( )A、
A、 B、 C、 D、10. 已知二次函数和一次函数 , 则这两个函数在同一个平面直角坐标系中的大致图象是( )A、 B、
B、 C、
C、 D、
D、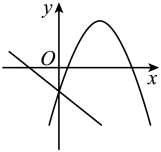
二、填空题
-
11. 二次根式 在实数范围内有意义,则x的取值范围是 .
12. 因式分解: =.13. 我国的长城始建于西周时期,被国务院确定为全国重点文物保护单位.长城总长约6700000米,数据6700000用科学记数法表示为.14. 一个不透明的袋子里装有2个红球和6个黑球,它们除颜色外其余都相同.从袋中任意摸出一个球是红球的概率为 .15. 如图,在菱形中, , , 则菱形的面积等于. 16. 如图,正五边形内接于 , 点F在劣弧上,则的度数为 °.
16. 如图,正五边形内接于 , 点F在劣弧上,则的度数为 °. 17. 如图,点A在双曲线上,点B在双曲线上,点A在点B的左侧,轴,点C,D在x轴上,若四边形为面积是9的矩形,则k的值为.
17. 如图,点A在双曲线上,点B在双曲线上,点A在点B的左侧,轴,点C,D在x轴上,若四边形为面积是9的矩形,则k的值为. 18. 如图,已知一个量角器的直径与正方形的边长相等,点N与点C重合,量角器的半圆弧与边交于点P,过点M作 , 交边于 , 连结 , 在量角器绕点C顺时针旋转的过程中,若的度数为 , 则°,此时的值为.
18. 如图,已知一个量角器的直径与正方形的边长相等,点N与点C重合,量角器的半圆弧与边交于点P,过点M作 , 交边于 , 连结 , 在量角器绕点C顺时针旋转的过程中,若的度数为 , 则°,此时的值为.
三、解答题
-
19. 计算.20. 先化简,再求值: , 其中.21. 如图,在四边形中, , , 平分 , 连接交于点 , 过点作交延长线于点 .
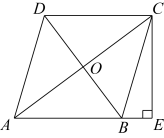 (1)、求证:四边形为菱形;(2)、若 , , 求的长.22. 如图所示,体育场内一看台与地面所成夹角为 , 看台最低点A到最高点B的距离米,A,B两点正前方有垂直于地面的旗杆 , 在A,B两点处用仪器测量旗杆顶端E的仰角分别为和.
(1)、求证:四边形为菱形;(2)、若 , , 求的长.22. 如图所示,体育场内一看台与地面所成夹角为 , 看台最低点A到最高点B的距离米,A,B两点正前方有垂直于地面的旗杆 , 在A,B两点处用仪器测量旗杆顶端E的仰角分别为和. (1)、求的长;(2)、求旗杆的高.23. 某校积极落实“双减”政策,将要开设拓展课程.为让学生可以根据自己的兴趣爱好选择最喜欢的课程,进行问卷调查,问卷设置以下四种选项:A(综合模型)、B(摄影艺术)、C(音乐鉴赏)、D(劳动实践),随机抽取了部分学生进行调查,每名学生必须且只能选择其中最喜欢的一种课程,并将调查结果整理绘制成如下不完整的统计图.
(1)、求的长;(2)、求旗杆的高.23. 某校积极落实“双减”政策,将要开设拓展课程.为让学生可以根据自己的兴趣爱好选择最喜欢的课程,进行问卷调查,问卷设置以下四种选项:A(综合模型)、B(摄影艺术)、C(音乐鉴赏)、D(劳动实践),随机抽取了部分学生进行调查,每名学生必须且只能选择其中最喜欢的一种课程,并将调查结果整理绘制成如下不完整的统计图.
根据以上信息,解答下列问题:
(1)、此次被调查的学生人数为名;(2)、直接在答题卡中补全条形统计图;(3)、求拓展课程D(劳动实践)所对应的扇形的圆心角的度数;(4)、根据抽样调查结果,请你估计该校1500名学生中,有多少名学生最喜欢C(音乐鉴赏)拓展课程.24. 如图,直线的图像与x轴,y轴分别交于点B,A,点B与点C关于原点对称,反比例函数的图像经过平行四边形的顶点D. (1)、求点C的坐标及反比例函数的解析式;(2)、动点M从点A到点D,动点N从点C到点A,都以每秒1个单位的速度运动,设运动时间为t秒,当t为何值时,四边形的面积最小?此时四边形的面积是多少?
(1)、求点C的坐标及反比例函数的解析式;(2)、动点M从点A到点D,动点N从点C到点A,都以每秒1个单位的速度运动,设运动时间为t秒,当t为何值时,四边形的面积最小?此时四边形的面积是多少?

