湖南省岳阳市岳阳县九校联考2023年第一次模拟考试数学试卷
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
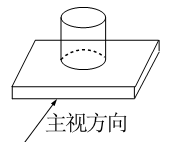
1. 实数﹣2023的绝对值是( )A、2023 B、﹣2023 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 如图所示的几何体是由一个圆柱和一个长方体组成的,它的主视图是( )
 A、
A、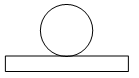 B、
B、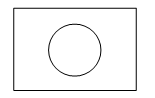 C、
C、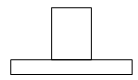 D、
D、 4. 若一元二次方程 有两个不相等的实数根,则实数a的取值范围是( )A、 B、 C、 且 D、 且5. 一个正六边形的内角和的度数为( )A、1080° B、720° C、540° D、360°6. 如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=25°,则∠CAD的度数是( )
4. 若一元二次方程 有两个不相等的实数根,则实数a的取值范围是( )A、 B、 C、 且 D、 且5. 一个正六边形的内角和的度数为( )A、1080° B、720° C、540° D、360°6. 如图,△ABC内接于⊙O,AD是⊙O的直径,∠ABC=25°,则∠CAD的度数是( ) A、25° B、60° C、65° D、75°7. 下列命题是假命题的是( )A、在同圆或等圆中,同一条弦所对的圆周角相等 B、圆内接四边形的对角互补 C、三角形的内心到三边的距离相等 D、三角形的外心是三边垂直平分线的交点8. 已知二次函数 , 若关于x的方程的实数根为a,β,且 , 则下列不等式正确的是( )A、 B、 C、 D、
A、25° B、60° C、65° D、75°7. 下列命题是假命题的是( )A、在同圆或等圆中,同一条弦所对的圆周角相等 B、圆内接四边形的对角互补 C、三角形的内心到三边的距离相等 D、三角形的外心是三边垂直平分线的交点8. 已知二次函数 , 若关于x的方程的实数根为a,β,且 , 则下列不等式正确的是( )A、 B、 C、 D、二、填空题
-
9. 分解因式:x3-x= .10. 根据相关数据显示,参加2023年全国初中毕业会考的考生预计在人以上,用科学记数法表示是.11. 二次函数的顶点坐标是.12. 已知 , 则代数式的值是.13. 如图,图形甲与图形乙是位似图形,O是位似中心,位似比为2:3,点A,B的对应点分别为点.若 , 则的长为.
 14. 如图,与的边相切,切点为B.将绕点B按顺时针方向旋转得到 , 使点落在上,边交线段于点C.若 , 则度.
14. 如图,与的边相切,切点为B.将绕点B按顺时针方向旋转得到 , 使点落在上,边交线段于点C.若 , 则度.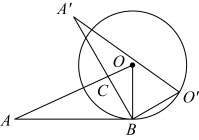 15. 已知圆锥的底面圆半径是3,高为4,则圆锥的侧面积是.16. 如图,是的直径,点C是上一点,与过点C的切线垂直,垂足为点D,切线与的延长线相交于点P,弦平分 , 交于点F,连接 ,
15. 已知圆锥的底面圆半径是3,高为4,则圆锥的侧面积是.16. 如图,是的直径,点C是上一点,与过点C的切线垂直,垂足为点D,切线与的延长线相交于点P,弦平分 , 交于点F,连接 , (1)、若 , , 则 弧的长为.(2)、若 , , 则的长为.
(1)、若 , , 则 弧的长为.(2)、若 , , 则的长为.三、解答题
-
17. 计算:18. 如图,点D为的边的中点,过点D作 , 交于点E,延长至点F,使 , 求证:.
 19. 反比例函数y= (k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
19. 反比例函数y= (k为常数,且k≠0)的图象经过点A(1,3)、B(3,m). (1)、求反比例函数的解析式及B点的坐标;(2)、在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.20. 4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然正气”.某校响应号召,开展了“读红色经典,传革命精神”为主题的读书活动,学校对本校学生五月份阅读该主题相关书籍的读书量进行了随机抽样调查,并对所有随机抽取的学生的读书量(单位:本)进行了统计.根据调查结果,绘制了不完整的统计表和扇形统计图.
(1)、求反比例函数的解析式及B点的坐标;(2)、在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.20. 4月23日是世界读书日,习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然正气”.某校响应号召,开展了“读红色经典,传革命精神”为主题的读书活动,学校对本校学生五月份阅读该主题相关书籍的读书量进行了随机抽样调查,并对所有随机抽取的学生的读书量(单位:本)进行了统计.根据调查结果,绘制了不完整的统计表和扇形统计图.读书量
1本
2本
3本
4本
5本
人数
10人
25人
30人
a
15人
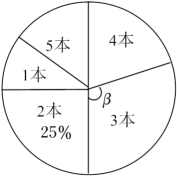 (1)、本次调查共抽取学生多少人?(2)、表中a的值为 , 扇形统计图中“3本”部分所对应的圆心角β的度数为 .(3)、已知该校有3000名学生,请估计该校学生中,五月份读书量不少于“3本”的学生人数.21. 建设美丽城市,改造老旧小区.某市2019年投入资金1000万元,2021年投入资金1440万元,现假定每年投入资金的增长率相同.(1)、求该市改造老旧小区投入资金的年平均增长率;(2)、2021年老旧小区改造的平均费用为每个80万元.2022年为提高老旧小区品质,每个小区改造费用增加15%.如果投入资金年增长率保持不变,求该市在2022年最多可以改造多少个老旧小区?22. 如图,为了测量河对岸A,B两点间的距离,数学兴趣小组在河岸南侧选定观测点C,测得A,B均在C的北偏东37°方向上,沿正东方向行走90米至观测点D,测得A在D的正北方向,B在D的北偏西53°方向上.求A,B两点间的距离.参考数据: , , .
(1)、本次调查共抽取学生多少人?(2)、表中a的值为 , 扇形统计图中“3本”部分所对应的圆心角β的度数为 .(3)、已知该校有3000名学生,请估计该校学生中,五月份读书量不少于“3本”的学生人数.21. 建设美丽城市,改造老旧小区.某市2019年投入资金1000万元,2021年投入资金1440万元,现假定每年投入资金的增长率相同.(1)、求该市改造老旧小区投入资金的年平均增长率;(2)、2021年老旧小区改造的平均费用为每个80万元.2022年为提高老旧小区品质,每个小区改造费用增加15%.如果投入资金年增长率保持不变,求该市在2022年最多可以改造多少个老旧小区?22. 如图,为了测量河对岸A,B两点间的距离,数学兴趣小组在河岸南侧选定观测点C,测得A,B均在C的北偏东37°方向上,沿正东方向行走90米至观测点D,测得A在D的正北方向,B在D的北偏西53°方向上.求A,B两点间的距离.参考数据: , , . 23.
23. (1)、如图1,在中,D,E,F分别为上的点,交于点G,求证: .(2)、如图2,在(1)的条件下,连接 . 若 , 求的值.(3)、如图3,在中,与交于点O,E为上一点,交于点G,交于点F.若平分 , 求的长.24. 如图,抛物线与x轴相交于点A、点B,与y轴相交于点C.
(1)、如图1,在中,D,E,F分别为上的点,交于点G,求证: .(2)、如图2,在(1)的条件下,连接 . 若 , 求的值.(3)、如图3,在中,与交于点O,E为上一点,交于点G,交于点F.若平分 , 求的长.24. 如图,抛物线与x轴相交于点A、点B,与y轴相交于点C. (1)、请直接写出点A,B,C的坐标;(2)、若点P是抛物线段上的一点,当的面积最大时求出点P的坐标,并求出面积的最大值.(3)、点F是抛物线上的动点,作交x轴于点E,是否存在点F,使得以A、C、E、F为顶点的四边形是平行四边形?若存在,请写出所有符合条件的点F的坐标;若不存在,请说明理由.
(1)、请直接写出点A,B,C的坐标;(2)、若点P是抛物线段上的一点,当的面积最大时求出点P的坐标,并求出面积的最大值.(3)、点F是抛物线上的动点,作交x轴于点E,是否存在点F,使得以A、C、E、F为顶点的四边形是平行四边形?若存在,请写出所有符合条件的点F的坐标;若不存在,请说明理由.