湖南省湘西凤凰县2023年九年级下学期初中学情诊断数学试卷
试卷更新日期:2023-05-04 类型:中考模拟
一、单选题
-
1. 2023的相反数是( )A、 B、 C、 D、20232. 据统计数据显示,2023年春节,凤凰古城接待游客564200人次,其中564200用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 初中生骑电动车上学存在安全隐患,为了解某初中2400个学生家长对“中学生骑电动车上学”的态度,从中随机调查200个家长,结果有180个家长持反对态度,则下列说法正确的是( )A、调查方式是普查 B、该校只有180个家长持反对态度 C、样本是200个家长 D、该校约有90%的家长持反对态度5. 若一个多边形的内角和等于 ,这个多边形的边数是( )A、6 B、8 C、10 D、126. 如图是由5个完全相同的小正方体组成的立体图形,则它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 7. 下列图象中,表示正比例函数图象的是( )A、
7. 下列图象中,表示正比例函数图象的是( )A、 B、
B、 C、
C、 D、
D、 8. 不等式组 的解集在数轴上表示正确的是( )A、
8. 不等式组 的解集在数轴上表示正确的是( )A、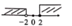 B、
B、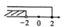 C、
C、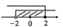 D、
D、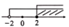 9. 如图,四边形ABCD是萎形,对角线AC、BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=25°,则∠DHO的度数是( )
9. 如图,四边形ABCD是萎形,对角线AC、BD相交于点O,DH⊥AB于点H,连接OH,∠CAD=25°,则∠DHO的度数是( ) A、25° B、30° C、35° D、40°10. 已知二次函数的图象如图所示,下列结论①;②;③;④ , 其中正确的是( )
A、25° B、30° C、35° D、40°10. 已知二次函数的图象如图所示,下列结论①;②;③;④ , 其中正确的是( ) A、①③④ B、①②④ C、①④ D、②③④
A、①③④ B、①②④ C、①④ D、②③④二、填空题
-
11. 若式子在实数范围内有意义,则实数的取值范围是.12. 分解因式:.13. 已知方程 ,则 .14. 如图,直线AB//CD, , , 则.
 15. 一个不诱明口袋里装有8个小球,其中黑球6个,白球2个,除颜色外均相同,从袋子中随机摸出一个小球,则摸出的小球是黑球的概率是 .16. 人数相同的甲乙两班学生在同一次数学单元测试中,班级平均分和方差如下:=85,s甲2=25,s乙2=16,则成绩较为稳定的班级是.17. 我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为a,b,c,记 ,则其面积 .这个公式也被称为海伦 秦九韶公式.若 , ,则此三角形面积的最大值为.18. 如图,在平面直角坐标系中,抛物线经过平移得到抛物线 , 其对称轴与两段抛物线所围成的阴影部分的面积为 .
15. 一个不诱明口袋里装有8个小球,其中黑球6个,白球2个,除颜色外均相同,从袋子中随机摸出一个小球,则摸出的小球是黑球的概率是 .16. 人数相同的甲乙两班学生在同一次数学单元测试中,班级平均分和方差如下:=85,s甲2=25,s乙2=16,则成绩较为稳定的班级是.17. 我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为a,b,c,记 ,则其面积 .这个公式也被称为海伦 秦九韶公式.若 , ,则此三角形面积的最大值为.18. 如图,在平面直角坐标系中,抛物线经过平移得到抛物线 , 其对称轴与两段抛物线所围成的阴影部分的面积为 .
三、解答题
-
19. 计算:.20. 先化简,再求值 ,其中21. 如图,反比例函数的图象与正比例函数的图象交于、B两点.点在反比例函数图象上,连接 , 交y轴于点N.
 (1)、求反比例函数的解析式.(2)、求的面积.22. 初三年级“黄金分割项目活动”展示,为了解全体初三年级同学的活动成绩,抽取了部分参加活动的同学的成绩进行统计后,分为“优秀”,“良好”,“一般”,“较差”四个等级,并根据成绩绘制成如图两幅不完整的统计图,请结合统计图中的信息,回答下列问题:
(1)、求反比例函数的解析式.(2)、求的面积.22. 初三年级“黄金分割项目活动”展示,为了解全体初三年级同学的活动成绩,抽取了部分参加活动的同学的成绩进行统计后,分为“优秀”,“良好”,“一般”,“较差”四个等级,并根据成绩绘制成如图两幅不完整的统计图,请结合统计图中的信息,回答下列问题: (1)、扇形统计图中“优秀”所对应扇形的圆心角为 度,并将条形统计图补充完整.(2)、如果学校初三年级共有340名学生,则参加“黄金分割项目活动”比赛成绩良好的学生有人.(3)、此次活动中有四名同学获得满分,分别是甲,乙,丙,丁,现从这四名同学中挑选网名同学参加校外举行的“黄金分割项目活动”展示,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.23. 图1是一台手机支架,图2是其侧面示意图,AB,BC可分别绕点A,B转动,测得 , , , .
(1)、扇形统计图中“优秀”所对应扇形的圆心角为 度,并将条形统计图补充完整.(2)、如果学校初三年级共有340名学生,则参加“黄金分割项目活动”比赛成绩良好的学生有人.(3)、此次活动中有四名同学获得满分,分别是甲,乙,丙,丁,现从这四名同学中挑选网名同学参加校外举行的“黄金分割项目活动”展示,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.23. 图1是一台手机支架,图2是其侧面示意图,AB,BC可分别绕点A,B转动,测得 , , , . (1)、在图2中,过点B作 , 垂足为E,填空:°;(2)、求点C到的距离.(结果保留小数点后一位,参考数据: , , , )24. 某学校为开展“阳光体育”活动,计划拿出不超过3000元的资金购买一批篮球、羽毛球拍和乒乓球拍,已知篮球、羽毛球拍和乒乓球拍的单价比为8︰3︰2,且其单价和为130元.(1)、 请问篮球、羽毛球拍和乒乓球拍的单价分别是多少元?(2)、 若要求购买篮球、羽毛球拍和乒乓球拍的总数量是80个(副),羽毛球拍的数量是篮球数量的4倍,且购买乒乓球拍的数量不超过15副,请问有几种购买方案?25. 如图,AB为⊙O的直径,C,D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.
(1)、在图2中,过点B作 , 垂足为E,填空:°;(2)、求点C到的距离.(结果保留小数点后一位,参考数据: , , , )24. 某学校为开展“阳光体育”活动,计划拿出不超过3000元的资金购买一批篮球、羽毛球拍和乒乓球拍,已知篮球、羽毛球拍和乒乓球拍的单价比为8︰3︰2,且其单价和为130元.(1)、 请问篮球、羽毛球拍和乒乓球拍的单价分别是多少元?(2)、 若要求购买篮球、羽毛球拍和乒乓球拍的总数量是80个(副),羽毛球拍的数量是篮球数量的4倍,且购买乒乓球拍的数量不超过15副,请问有几种购买方案?25. 如图,AB为⊙O的直径,C,D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.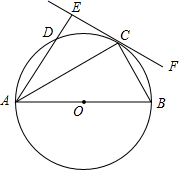 (1)、求证:EF是⊙O的切线.(2)、若∠CAO=30°,BC=2,求劣弧BC的长.26. 综合与探究:如图,在平面直角坐标系中,抛物线与x轴交于点 , , 与y轴交于点C,连接.若在第四象限的抛物线上取一点M,过点M作轴于点D,交直线于点E.
(1)、求证:EF是⊙O的切线.(2)、若∠CAO=30°,BC=2,求劣弧BC的长.26. 综合与探究:如图,在平面直角坐标系中,抛物线与x轴交于点 , , 与y轴交于点C,连接.若在第四象限的抛物线上取一点M,过点M作轴于点D,交直线于点E. (1)、求抛物线的表达式;(2)、试探究抛物线上是否存在点M,使有最大值?若存在,求出点M的坐标和的最大值;若不存在,请说明理由;(3)、连接 , 试探究是否存在点M,使得以M,C,E为顶点的三角形和相似?若存在,请求出点M的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、试探究抛物线上是否存在点M,使有最大值?若存在,求出点M的坐标和的最大值;若不存在,请说明理由;(3)、连接 , 试探究是否存在点M,使得以M,C,E为顶点的三角形和相似?若存在,请求出点M的坐标;若不存在,请说明理由.